Vector-radix FFT algorithm

From HandWiki

The vector-radix FFT algorithm, is a multidimensional fast Fourier transform (FFT) algorithm, which is a generalization of the ordinary Cooley–Tukey FFT algorithm that divides the transform dimensions by arbitrary radices. It breaks a multidimensional (MD) discrete Fourier transform (DFT) down into successively smaller MD DFTs until, ultimately, only trivial MD DFTs need to be evaluated.[1] The most common multidimensional FFT algorithm is the row-column algorithm, which means transforming the array first in one index and then in the other, see more in FFT. Then a radix-2 direct 2-D FFT has been developed,[2] and it can eliminate 25% of the multiplies as compared to the conventional row-column approach. And this algorithm has been extended to rectangular arrays and arbitrary radices,[3] which is the general vector-radix algorithm.

Vector-radix FFT algorithm can reduce the number of complex multiplications significantly, compared to row-vector algorithm. For example, for a [math]\displaystyle{ N^M }[/math] element matrix (M dimensions, and size N on each dimension), the number of complex multiples of vector-radix FFT algorithm for radix-2 is [math]\displaystyle{ \frac{2^M -1}{2^M} N^M \log_2 N }[/math], meanwhile, for row-column algorithm, it is [math]\displaystyle{ \frac{M N^M} 2 \log_2 N }[/math]. And generally, even larger savings in multiplies are obtained when this algorithm is operated on larger radices and on higher dimensional arrays.[3]

Overall, the vector-radix algorithm significantly reduces the structural complexity of the traditional DFT having a better indexing scheme, at the expense of a slight increase in arithmetic operations. So this algorithm is widely used for many applications in engineering, science, and mathematics, for example, implementations in image processing,[4] and high speed FFT processor designing.[5]

2-D DIT case

As with the Cooley–Tukey FFT algorithm, the two dimensional vector-radix FFT is derived by decomposing the regular 2-D DFT into sums of smaller DFT's multiplied by "twiddle" factors.

A decimation-in-time (DIT) algorithm means the decomposition is based on time domain [math]\displaystyle{ x }[/math], see more in Cooley–Tukey FFT algorithm.

We suppose the 2-D DFT is defined

[math]\displaystyle{ X(k_1,k_2) = \sum_{n_1=0}^{N_1-1} \sum_{n_2=0}^{N_2-1} x[n_1, n_2] \cdot W_{N_1}^{k_1 n_1} W_{N_2}^{k_2 n_2}, }[/math]

where [math]\displaystyle{ k_1 = 0,\dots,N_1-1 }[/math],and [math]\displaystyle{ k_2 = 0,\dots,N_2-1 }[/math], and [math]\displaystyle{ x[n_1, n_2] }[/math] is an [math]\displaystyle{ N_1 \times N_2 }[/math] matrix, and [math]\displaystyle{ W_N = \exp(-j 2\pi /N) }[/math].

For simplicity, let us assume that [math]\displaystyle{ N_1=N_2=N }[/math], and the radix-[math]\displaystyle{ (r\times r) }[/math] is such that [math]\displaystyle{ N/r }[/math] is an integer.

Using the change of variables:

  • [math]\displaystyle{ n_i=rp_i+q_i }[/math], where [math]\displaystyle{ p_i=0,\ldots,(N/r)-1; q_i = 0,\ldots,r-1; }[/math]
  • [math]\displaystyle{ k_i=u_i+v_i N/r }[/math], where [math]\displaystyle{ u_i=0,\ldots,(N/r)-1; v_i = 0,\ldots,r-1; }[/math]

where [math]\displaystyle{ i = 1 }[/math] or [math]\displaystyle{ 2 }[/math], then the two dimensional DFT can be written as:[6]

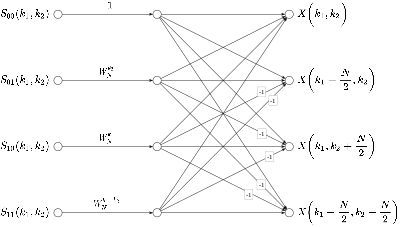
[math]\displaystyle{ X(u_1+v_1 N/r,u_2+v_2 N/r)=\sum_{q_1=0}^{r-1} \sum_{q_2=0}^{r-1} \left[ \sum_{p_1=0}^{N/r-1} \sum_{p_2=0}^{N/r-1} x[rp_1+q_1, rp_1+q_1] W_{N/r}^{p_1 u_1} W_{N/r}^{p_2 u_2} \right] \cdot W_N^{q_1 u_1+q_2 u_2} W_r^{q_1 v_1} W_r^{q_2 v_2}, }[/math]
One stage "butterfly" for DIT vector-radix 2x2 FFT

The equation above defines the basic structure of the 2-D DIT radix-[math]\displaystyle{ (r\times r) }[/math] "butterfly". (See 1-D "butterfly" in Cooley–Tukey FFT algorithm)

When [math]\displaystyle{ r=2 }[/math], the equation can be broken into four summations, and this leads to:[1]

[math]\displaystyle{ X(k_1,k_2) = S_{00}(k_1,k_2) + S_{01}(k_1,k_2) W_N^{k_2} +S_{10}(k_1,k_2) W_N^{k_1} + S_{11}(k_1,k_2) W_N^{k_1+k_2} }[/math] for [math]\displaystyle{ 0\leq k_1, k_2 \lt \frac{N}{2} }[/math],

where [math]\displaystyle{ S_{ij}(k_1,k_2)=\sum_{n_1=0}^{N/2-1} \sum_{n_2=0}^{N/2-1} x[2 n_1 + i, 2 n_2 + j] \cdot W_{N/2}^{n_1 k_1} W_{N/2}^{n_2 k_2} }[/math].

The [math]\displaystyle{ S_{ij} }[/math] can be viewed as the [math]\displaystyle{ N/2 }[/math]-dimensional DFT, each over a subset of the original sample:

  • [math]\displaystyle{ S_{00} }[/math] is the DFT over those samples of [math]\displaystyle{ x }[/math] for which both [math]\displaystyle{ n_1 }[/math] and [math]\displaystyle{ n_2 }[/math] are even;
  • [math]\displaystyle{ S_{01} }[/math] is the DFT over the samples for which [math]\displaystyle{ n_1 }[/math] is even and [math]\displaystyle{ n_2 }[/math] is odd;
  • [math]\displaystyle{ S_{10} }[/math] is the DFT over the samples for which [math]\displaystyle{ n_1 }[/math] is odd and [math]\displaystyle{ n_2 }[/math] is even;
  • [math]\displaystyle{ S_{11} }[/math] is the DFT over the samples for which both [math]\displaystyle{ n_1 }[/math] and [math]\displaystyle{ n_2 }[/math] are odd.

Thanks to the periodicity of the complex exponential, we can obtain the following additional identities, valid for [math]\displaystyle{ 0\leq k_1, k_2 \lt \frac{N}{2} }[/math]:

  • [math]\displaystyle{ X\biggl(k_1+\frac{N}{2},k_2\biggr) = S_{00}(k_1,k_2) + S_{01}(k_1,k_2) W_N^{k_2} -S_{10}(k_1,k_2) W_N^{k_1} - S_{11}(k_1,k_2) W_N^{k_1+k_2} }[/math];
  • [math]\displaystyle{ X\biggl(k_1,k_2+\frac{N}{2}\biggr) = S_{00}(k_1,k_2) - S_{01}(k_1,k_2) W_N^{k_2} +S_{10}(k_1,k_2) W_N^{k_1} - S_{11}(k_1,k_2) W_N^{k_1+k_2} }[/math];
  • [math]\displaystyle{ X\biggl(k_1+\frac{N}{2},k_2+\frac{N}{2}\biggr) = S_{00}(k_1,k_2) - S_{01}(k_1,k_2) W_N^{k_2} -S_{10}(k_1,k_2) W_N^{k_1} + S_{11}(k_1,k_2) W_N^{k_1+k_2} }[/math].

2-D DIF case

Similarly, a decimation-in-frequency (DIF, also called the Sande–Tukey algorithm) algorithm means the decomposition is based on frequency domain [math]\displaystyle{ X }[/math], see more in Cooley–Tukey FFT algorithm.

Using the change of variables:

  • [math]\displaystyle{ n_i=p_i+q_i N/r }[/math], where [math]\displaystyle{ p_i=0,\ldots,(N/r)-1; q_i = 0,\ldots,r-1; }[/math]
  • [math]\displaystyle{ k_i=r u_i+v_i }[/math], where [math]\displaystyle{ u_i=0,\ldots,(N/r)-1; v_i = 0,\ldots,r-1; }[/math]

where [math]\displaystyle{ i = 1 }[/math] or [math]\displaystyle{ 2 }[/math], and the DFT equation can be written as:[6]

[math]\displaystyle{ X(r u_1+v_1,r u_2+v_2)=\sum_{p_1=0}^{N/r-1} \sum_{p_2=0}^{N/r-1} \left[ \sum_{q_1=0}^{r-1} \sum_{q_2=0}^{r-1} x[p_1+q_1 N/r, p_1+q_1 N/r] W_{r}^{q_1 v_1} W_{r}^{q_2 v_2} \right] \cdot W_{N}^{p_1 v_1+p_2 v_2} W_{N/r}^{p_1 u_1} W_{N/r}^{p_2 u_2}, }[/math]

Other approaches

The split-radix FFT algorithm has been proved to be a useful method for 1-D DFT. And this method has been applied to the vector-radix FFT to obtain a split vector-radix FFT.[6][7]

In conventional 2-D vector-radix algorithm, we decompose the indices [math]\displaystyle{ k_1,k_2 }[/math] into 4 groups:

[math]\displaystyle{ \begin{array}{lcl} X(2 k_1, 2 k_2) & : & \text{even-even} \\ X(2 k_1, 2 k_2 +1) & : & \text{even-odd} \\ X(2 k_1 +1, 2 k_2) & : & \text{odd-even} \\ X(2 k_1+1, 2 k_2+1) & : & \text{odd-odd} \end{array} }[/math]

By the split vector-radix algorithm, the first three groups remain unchanged, the fourth odd-odd group is further decomposed into another four sub-groups, and seven groups in total:

[math]\displaystyle{ \begin{array}{lcl} X(2 k_1, 2 k_2) & : & \text{even-even} \\ X(2 k_1, 2 k_2 +1) & : & \text{even-odd} \\ X(2 k_1 +1, 2 k_2) & : & \text{odd-even} \\ X(4 k_1+1, 4 k_2+1) & : & \text{odd-odd} \\ X(4 k_1+1, 4 k_2+3) & : & \text{odd-odd} \\ X(4 k_1+3, 4 k_2+1) & : & \text{odd-odd} \\ X(4 k_1+3, 4 k_2+3) & : & \text{odd-odd} \end{array} }[/math]

That means the fourth term in 2-D DIT radix-[math]\displaystyle{ (2\times 2) }[/math] equation, [math]\displaystyle{ S_{11}(k_1,k_2) W_{N}^{k_1+k_2} }[/math] becomes:[8]

[math]\displaystyle{ A_{11}(k_1,k_2) W_N^{k_1+k_2} + A_{13}(k_1,k_2) W_N^{k_1+3 k_2} +A_{31}(k_1,k_2) W_N^{3 k_1+k_2} + A_{33}(k_1,k_2) W_N^{3(k_1+k_2)}, }[/math]

where [math]\displaystyle{ A_{ij}(k_1,k_2)=\sum_{n_1=0}^{N/4-1} \sum_{n_2=0}^{N/4-1} x[4 n_1 + i, 4 n_2 + j] \cdot W_{N/4}^{n_1 k_1} W_{N/4}^{n_2 k_2} }[/math]

The 2-D N by N DFT is then obtained by successive use of the above decomposition, up to the last stage.

It has been shown that the split vector radix algorithm has saved about 30% of the complex multiplications and about the same number of the complex additions for typical [math]\displaystyle{ 1024\times 1024 }[/math] array, compared with the vector-radix algorithm.[7]

References

  1. ↑ 1.0 1.1 Dudgeon, Dan; Russell, Mersereau (September 1983). Multidimensional Digital Signal Processing. Prentice Hall. pp. 76. ISBN 0136049591. 
  2. ↑ Rivard, G. (1977). "Direct fast Fourier transform of bivariate functions". IEEE Transactions on Acoustics, Speech, and Signal Processing 25 (3): 250–252. doi:10.1109/TASSP.1977.1162951. 
  3. ↑ 3.0 3.1 Harris, D.; McClellan, J.; Chan, D.; Schuessler, H. (1977). "Vector radix fast Fourier transform". ICASSP '77. IEEE International Conference on Acoustics, Speech, and Signal Processing. 2. pp. 548–551. doi:10.1109/ICASSP.1977.1170349. 
  4. ↑ Buijs, H.; Pomerleau, A.; Fournier, M.; Tam, W. (Dec 1974). "Implementation of a fast Fourier transform (FFT) for image processing applications". IEEE Transactions on Acoustics, Speech, and Signal Processing 22 (6): 420–424. doi:10.1109/TASSP.1974.1162620. 
  5. ↑ Badar, S.; Dandekar, D. (2015). "High speed FFT processor design using radix −4 pipelined architecture". 2015 International Conference on Industrial Instrumentation and Control (ICIC). pp. 1050–1055. doi:10.1109/IIC.2015.7150901. ISBN 978-1-4799-7165-7. 
  6. ↑ 6.0 6.1 6.2 Chan, S. C.; Ho, K. L. (1992). "Split vector-radix fast Fourier transform". IEEE Transactions on Signal Processing 40 (8): 2029–2039. doi:10.1109/78.150004. Bibcode: 1992ITSP...40.2029C. 
  7. ↑ 7.0 7.1 Pei, Soo-Chang; Wu, Ja-Lin (April 1987). "Split vector radix 2D fast Fourier transform". ICASSP '87. IEEE International Conference on Acoustics, Speech, and Signal Processing. 12. pp. 1987–1990. doi:10.1109/ICASSP.1987.1169345. 
  8. ↑ Wu, H.; Paoloni, F. (Aug 1989). "On the two-dimensional vector split-radix FFT algorithm". IEEE Transactions on Acoustics, Speech, and Signal Processing 37 (8): 1302–1304. doi:10.1109/29.31283. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Vector-radix_FFT_algorithm&oldid=3431850"