Visual Information Fidelity

Short description: Objective full-reference image quality assessment index

Visual Information Fidelity (VIF) is a full reference image quality assessment index based on natural scene statistics and the notion of image information extracted by the human visual system. It was developed by Hamid R Sheikh and Alan Bovik at the Laboratory for Image and Video Engineering (LIVE) at the University of Texas at Austin in 2006. It is deployed in the core of the Netflix VMAF video quality monitoring system, which controls the picture quality of all encoded videos streamed by Netflix.

Model Overview

Specifically, the reference image is modeled as being the output of a stochastic `natural' source that passes through the HVS channel and is processed later by the brain. The information content of the reference image is quantified as being the mutual information between the input and output of the HVS channel. This is the information that the brain could ideally extract from the output of the HVS. The same measure is then quantified in the presence of an image distortion channel that distorts the output of the natural source before it passes through the HVS channel, thereby measuring the information that the brain could ideally extract from the test image. This is shown pictorially in Figure 1. The two information measures are then combined to form a visual information fidelity measure that relates visual quality to relative image information.

Figure 1

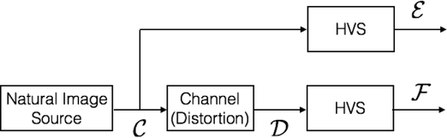
System Model

Source Model

A Gaussian scale mixture (GSM) is used to statistically model the wavelet coefficients of a steerable pyramid decomposition of an image. The model is described below for a given subband of the multi-scale multi-orientation decomposition and can be extended to other subbands similarly. Let the wavelet coefficients in a given subband be [math]\displaystyle{ \mathcal{C}=\{\bar{C}_i:i\in\mathcal{I}\} }[/math] where [math]\displaystyle{ \mathcal{I} }[/math] denotes the set of spatial indices across the subband and each [math]\displaystyle{ \bar{C}_i }[/math] is an [math]\displaystyle{ M }[/math] dimensional vector. The subband is partitioned into non-overlapping blocks of [math]\displaystyle{ M }[/math] coefficients each, where each block corresponds to [math]\displaystyle{ \bar{C}_i }[/math]. According to the GSM model, [math]\displaystyle{ \mathcal{C} = \mathcal{S}\cdot\mathcal{U} = \{S_i\bar{U}_i:i\in\mathcal{I}\}, }[/math] where [math]\displaystyle{ S_i }[/math] is a positive scalar and [math]\displaystyle{ \bar{U}_i }[/math] is a Gaussian vector with mean zero and co-variance [math]\displaystyle{ \mathbf{C}_U }[/math]. Further the non-overlapping blocks are assumed to be independent of each other and that the random field [math]\displaystyle{ \mathcal{S} }[/math] is independent of [math]\displaystyle{ \mathcal{U} }[/math].

Distortion Model

The distortion process is modeled using a combination of signal attenuation and additive noise in the wavelet domain. Mathematically, if [math]\displaystyle{ \mathcal{D}=\{\bar{D}_i:i\in\mathcal{I}\} }[/math] denotes the random field from a given subband of the distorted image, [math]\displaystyle{ \mathcal{G}=\{g_i:i\in\mathcal{I}\} }[/math] is a deterministic scalar field and [math]\displaystyle{ \mathcal{V}=\{\bar{V}_i: i\in\mathcal{I}\} }[/math], where [math]\displaystyle{ \bar{V}_i }[/math] is a zero mean Gaussian vector with co-variance [math]\displaystyle{ \mathbf{C}_V=\sigma_v^2\mathbf{I} }[/math], then

[math]\displaystyle{ \mathcal{D}=\mathcal{G}\mathcal{C}+\mathcal{V}. }[/math]

Further, [math]\displaystyle{ \mathcal{V} }[/math] is modeled to be independent of [math]\displaystyle{ \mathcal{S} }[/math] and [math]\displaystyle{ \mathcal{U} }[/math].

HVS Model

The duality of HVS models and NSS implies that several aspects of the HVS have already been accounted for in the source model. Here, the HVS is additionally modeled based on the hypothesis that the uncertainty in the perception of visual signals limits the amount of information that can be extracted from the source and distorted image. This source of uncertainty can be modeled as visual noise in the HVS model. In particular, the HVS noise in a given subband of the wavelet decomposition is modeled as additive white Gaussian noise. Let [math]\displaystyle{ \mathcal{N}=\{\bar{N}_i:i\in\mathcal{I}\} }[/math] and [math]\displaystyle{ \mathcal{N}'=\{\bar{N}_i':i\in\mathcal{I}\} }[/math] be random fields, where [math]\displaystyle{ \bar{N}_i }[/math] and [math]\displaystyle{ \bar{N}_i' }[/math] are zero mean Gaussian vectors with co-variance [math]\displaystyle{ \mathbf{C}_N }[/math] and [math]\displaystyle{ \mathbf{C}_N' }[/math]. Further, let [math]\displaystyle{ \mathcal{E} }[/math] and [math]\displaystyle{ \mathcal{F} }[/math] denote the visual signal at the output of the HVS. Mathematically, we have [math]\displaystyle{ \mathcal{E}=\mathcal{C}+\mathcal{N} }[/math] and [math]\displaystyle{ \mathcal{F}=\mathcal{D}+\mathcal{N}' }[/math]. Note that [math]\displaystyle{ \mathcal{N} }[/math] and [math]\displaystyle{ \mathcal{N}' }[/math] are random fields that are independent of [math]\displaystyle{ \mathcal{S} }[/math], [math]\displaystyle{ \mathcal{U} }[/math] and [math]\displaystyle{ \mathcal{V} }[/math].

VIF Index

Let [math]\displaystyle{ \bar{C}^N=(\bar{C}_1,\bar{C}_2,\ldots,\bar{C}^N) }[/math] denote the vector of all blocks from a given subband. Let [math]\displaystyle{ S^N,\bar{D}^N,\bar{E}^N }[/math] and [math]\displaystyle{ \bar{F}^N }[/math] be similarly defined. Let [math]\displaystyle{ s^N }[/math] denote the maximum likelihood estimate of [math]\displaystyle{ S^N }[/math] given [math]\displaystyle{ C^N }[/math] and [math]\displaystyle{ \mathbf{C}_U }[/math]. The amount of information extracted from the reference is obtained as [math]\displaystyle{ I(\bar{C}^N;\bar{E}^N|\bar{S}^N=s^N) = \frac{1}{2}\sum_{i=1}^N\log_2\left(\frac{|s_i^2\mathbf{C}_U+\sigma_n^2\mathbf{I}|}{|\sigma_n^2\mathbf{I}|}\right), }[/math] while the amount of information extracted from the test image is given as [math]\displaystyle{ I(\bar{C}^N;\bar{F}^N|\bar{S}^N=s^N) = \frac{1}{2}\sum_{i=1}^N\log_2\left(\frac{|g_i^2s_i^2\mathbf{C}_U+(\sigma_v^2+\sigma_n^2)\mathbf{I}|}{|(\sigma_v^2+\sigma_n^2)\mathbf{I}|}\right). }[/math] Denoting the [math]\displaystyle{ N }[/math] blocks in subband [math]\displaystyle{ j }[/math] of the wavelet decomposition by [math]\displaystyle{ \bar{C}^{N,j} }[/math], and similarly for the other variables, the VIF index is defined as [math]\displaystyle{ \textrm{VIF} = \frac{\sum_{j\in\textrm{subbands}}I(\bar{C}^{N,j};\bar{F}^{N,j}|S^{N,j}=s^{N,j})}{\sum_{j\in\textrm{subbands}}I(\bar{C}^{N,j};\bar{E}^{N,j}|S^{N,j}=s^{N,j})}. }[/math]

Performance

The Spearman's rank-order correlation coefficient (SROCC) between the VIF index scores of distorted images on the LIVE Image Quality Assessment Database and the corresponding human opinion scores is evaluated to be 0.96.

External links

• Laboratory for Image and Video Engineering at the University of Texas
• An implementation of the VIF index
• LIVE Image Quality Assessment Database