Wavelet Tree

A wavelet tree on the string "abracadabra". At each node the symbols of the string are projected onto two partitions of the alphabet, and a bitvector denotes to which partition each symbol belongs. Note that only the bitvectors are stored; the strings in the nodes are only for illustratory purposes.

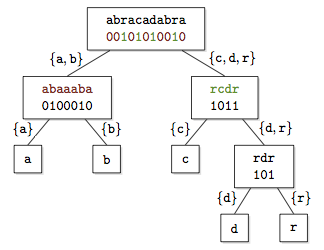
The Wavelet Tree is a succinct data structure to store strings in compressed space. It generalizes the [math]\displaystyle{ \mathbf{rank}_q }[/math] and [math]\displaystyle{ \mathbf{select}_q }[/math] operations defined on bitvectors to arbitrary alphabets.

Originally introduced to represent compressed suffix arrays, it has found application in several contexts. The tree is defined by recursively partitioning the alphabet into pairs of subsets; the leaves correspond to individual symbols of the alphabet, and at each node a bitvector stores whether a symbol of the string belongs to one subset or the other.

The name derives from an analogy with the wavelet transform for signals, which recursively decomposes a signal into low-frequency and high-frequency components.

Properties

Let [math]\displaystyle{ \Sigma }[/math] be a finite alphabet with [math]\displaystyle{ \sigma={|\Sigma|} }[/math]. By using succinct dictionaries in the nodes, a string [math]\displaystyle{ s \in \Sigma^* }[/math] can be stored in [math]\displaystyle{ {|s|}H_0(s) + o({|s|}\log \sigma) }[/math], where [math]\displaystyle{ H_0(s) }[/math] is the order-0 empirical entropy of [math]\displaystyle{ s }[/math].

If the tree is balanced, the operations [math]\displaystyle{ \mathbf{access} }[/math], [math]\displaystyle{ \mathbf{rank}_q }[/math], and [math]\displaystyle{ \mathbf{select}_q }[/math] can be supported in [math]\displaystyle{ O(\log \sigma) }[/math] time.

Access operation

A wavelet tree contains a bitmap representation of a string. If we know the alphabet set, then the exact string can be inferred by tracking bits down the tree. To find the letter at i^th position in the string :-

Algorithm access
  Input:
    - The position i in the string of which we want to know the letter, starting at 1.
    - The top node W of the wavelet tree that represents the string
  Output: The letter at position i

    if W.isLeafNode return W.letter
    if W.bitvector[i] = 0 return access(i - rank(W.bitvector, i), W.left)
    else return access(rank(W.bitvector, i), W.right)

• "←" denotes assignment. For instance, "largest ← item" means that the value of largest changes to the value of item.
• "return" terminates the algorithm and outputs the following value.

In this context, the rank of a position [math]\displaystyle{ i }[/math] in a bitvector [math]\displaystyle{ b }[/math] is the number of ones that appear in the first [math]\displaystyle{ i }[/math] positions of [math]\displaystyle{ b }[/math]. Because the rank can be calculated in O(1) by using succinct dictionaries, any S[i] in string S can be accessed in [math]\displaystyle{ O(\log \sigma) }[/math] time, as long as the tree is balanced.

Extensions

Several extensions to the basic structure have been presented in the literature. To reduce the height of the tree, multiary nodes can be used instead of binary. The data structure can be made dynamic, supporting insertions and deletions at arbitrary points of the string; this feature enables the implementation of dynamic FM-indexes. This can be further generalized, allowing the update operations to change the underlying alphabet: the Wavelet Trie exploits the trie structure on an alphabet of strings to enable dynamic tree modifications.

Further reading

• Wavelet Trees. A blog post describing the construction of a wavelet tree, with examples.