Wild arc

Short description: Embedding of the unit interval into 3-space ambient isotopy inequivalent to a line segment

This article is about a mathematical object. For animal rehabilitation, see Wild Animal Rehabilitation Center.

Fox-Artin arc Example 1.1

In geometric topology, a wild arc is an embedding of the unit interval into 3-dimensional space not equivalent to the usual one in the sense that there does not exist an ambient isotopy taking the arc to a straight line segment.

(Antoine 1920) found the first example of a wild arc. (Fox Artin) found another example, called the Fox-Artin arc, whose complement is not simply connected.

Fox-Artin arcs

Two very similar wild arcs appear in the (Fox Artin) article. Example 1.1 (page 981) is most generally referred to as the Fox-Artin wild arc. The crossings have the regular sequence over/over/under/over/under/under when following the curve from left to right.

The left end-point 0 of the closed unit interval $[0,1]$ is mapped by the arc to the left limit point of the curve, and 1 is mapped to the right limit point. The range of the arc lies in the Euclidean space ${\mathbb{ℝ}}^3$ or the 3-sphere $S^3$.

Fox-Artin arc variant

Fox-Artin arc Example 1.1*

Example 1.1* has the crossing sequence over/under/over/under/over/under. According to (Fox Artin), page 982: "This is just the chain stitch of knitting extended indefinitely in both directions."

This arc cannot be continuously deformed to produce Example 1.1 in ${\mathbb{ℝ}}^3$ or $S^3$, despite its similar appearance.

The Fox–Artin wild arc (Example 1.1*) lying in ${\mathbb{ℝ}}^3$ drawn as a knot diagram. Note that each "tail" of the arc is converging to a point.

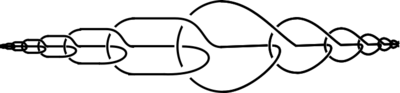
Also shown here is an alternative style of diagram for the arc in Example 1.1*.

See also

• Wild knot
• Alexander horned sphere

Further reading

• Antoine, L. (1920), "Sur la possibilité d'étendre l'homéomorphie de deux figures à leurs voisinages", C. R. Acad. Sci. Paris 171: 661 
• Fox, Ralph H.; Harrold, O. G. (1962), "The Wilder arcs", Topology of 3-manifolds and related topics (Proc. The Univ. of Georgia Institute, 1961), Prentice Hall, pp. 184–187 
• Fox, Ralph H.; Artin, Emil (1948), "Some wild cells and spheres in three-dimensional space", Annals of Mathematics, Second Series 49 (4): 979–990, doi:10.2307/1969408, ISSN 0003-486X 
• Hocking, John Gilbert; Young, Gail Sellers (1988). Topology. Dover. pp. 176–177. ISBN 0-486-65676-4. https://archive.org/details/topology00hock_0/page/176. 
• McPherson, James M. (1973), "Wild arcs in three-space. I. Families of Fox–Artin arcs", Pacific Journal of Mathematics 45 (2): 585–598, doi:10.2140/pjm.1973.45.585, ISSN 0030-8730, http://projecteuclid.org/euclid.pjm/1102947540