Singularity function

Short description: Class of discontinuous functions

Singularity functions are a class of discontinuous functions that contain singularities, i.e., they are discontinuous at their singular points. Singularity functions have been heavily studied in the field of mathematics under the alternative names of generalized functions and distribution theory. The functions are notated with brackets, as $⟨x-a{⟩}^n$ where n is an integer. The "$⟨⟩$" are often referred to as singularity brackets . The functions are defined as:

n	$⟨x-a{⟩}^n$
$<0$	$\frac{d^{|n+1|}}{d{x}^{|n+1|}}\delta (x-a)$
-2	$\frac{d}{dx}\delta (x-a)$
-1	$\delta (x-a)$
0	$H(x-a)$
1	$(x-a)H(x-a)$
2	$(x-a{)}^{2}H(x-a)$
$\ge 0$	$(x-a{)}^{n}H(x-a)$

where: δ(x) is the Dirac delta function, also called the unit impulse. The first derivative of δ(x) is also called the unit doublet. The function $H(x)$ is the Heaviside step function: H(x) = 0 for x < 0 and H(x) = 1 for x > 0. The value of H(0) will depend upon the particular convention chosen for the Heaviside step function. Note that this will only be an issue for n = 0 since the functions contain a multiplicative factor of x − a for n > 0. $⟨x-a{⟩}^1$ is also called the Ramp function.

Integration

Integrating $⟨x-a{⟩}^n$ can be done in a convenient way in which the constant of integration is automatically included so the result will be 0 at x = a.

$$\int ⟨x-a{⟩}^{n}dx=\{\begin{array}{ll}⟨x-a{⟩}^{n+1},& n<0\\ \frac{⟨x-a{⟩}^{n+1}}{n+1},& n\ge 0\end{array}$$

Example beam calculation

The deflection of a simply supported beam, as shown in the diagram, with constant cross-section and elastic modulus, can be found using Euler–Bernoulli beam theory. Here, we are using the sign convention of downward forces and sagging bending moments being positive.

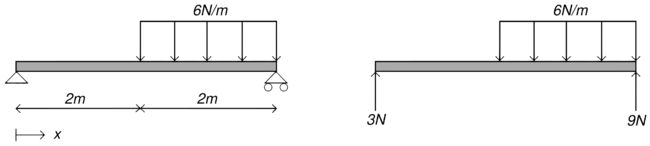
Load distribution:

$w=-3\text{ N}⟨x-0{⟩}^{-1}+6{\text{ Nm}}^{-1}⟨x-2\text{ m}{⟩}^0-9\text{ N}⟨x-4\text{ m}{⟩}^{-1}-6{\text{ Nm}}^{-1}⟨x-4\text{ m}{⟩}^0$

Shear force:

$S=\int wdx$

$S=-3\text{ N}⟨x-0{⟩}^0+6{\text{ Nm}}^{-1}⟨x-2\text{ m}{⟩}^1-9\text{ N}⟨x-4\text{ m}{⟩}^0-6{\text{ Nm}}^{-1}⟨x-4\text{ m}{⟩}^1$

Bending moment:

$M=-\int Sdx$

$M=3\text{ N}⟨x-0{⟩}^1-3{\text{ Nm}}^{-1}⟨x-2\text{ m}{⟩}^2+9\text{ N}⟨x-4\text{ m}{⟩}^1+3{\text{ Nm}}^{-1}⟨x-4\text{ m}{⟩}^2$

Slope:

$u^{\prime }=\frac{1}{EI}\int Mdx$

Because the slope is not zero at x = 0, a constant of integration, c, is added

$u^{\prime }=\frac{1}{EI}(\frac{3}{2}\text{ N}⟨x-0{⟩}^2-1{\text{ Nm}}^{-1}⟨x-2\text{ m}{⟩}^3+\frac{9}{2}\text{ N}⟨x-4\text{ m}{⟩}^2+1{\text{ Nm}}^{-1}⟨x-4\text{ m}{⟩}^3+c)$

Deflection:

$u=\int u^{\prime }dx$

$u=\frac{1}{EI}(\frac{1}{2}\text{ N}⟨x-0{⟩}^3-\frac{1}{4}{\text{ Nm}}^{-1}⟨x-2\text{ m}{⟩}^4+\frac{3}{2}\text{ N}⟨x-4\text{ m}{⟩}^3+\frac{1}{4}{\text{ Nm}}^{-1}⟨x-4\text{ m}{⟩}^4+cx)$

The boundary condition u = 0 at x = 4 m allows us to solve for c = −7 Nm²

See also

• Macaulay brackets
• Macaulay's method

External links

• Singularity Functions (Tim Lahey)
• Singularity functions (J. Lubliner, Department of Civil and Environmental Engineering)
• Beams: Deformation by Singularity Functions (Dr. Ibrahim A. Assakkaf)