Zhao Youqin's π algorithm
Zhao Youqin's π algorithm was an algorithm devised by Yuan dynasty Chinese astronomer and mathematician Zhao Youqin (赵友钦, ? – 1330) to calculate the value of π in his book Ge Xiang Xin Shu (革象新书).
Algorithm
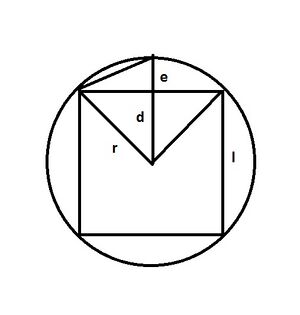
Zhao Youqin started with an inscribed square in a circle with radius r.[1]
If [math]\displaystyle{ \ell }[/math] denotes the length of a side of the square, draw a perpendicular line d from the center of the circle to side l. Let e denotes r − d. Then from the diagram:
- [math]\displaystyle{ d=\sqrt{r^2-\left(\frac{\ell}{2}\right)^2} }[/math]
- [math]\displaystyle{ e=r-d=r-\sqrt{r^2-\left(\frac{\ell}{2}\right)^2}. }[/math]
Extend the perpendicular line d to dissect the circle into an octagon; [math]\displaystyle{ \ell_2 }[/math] denotes the length of one side of octagon.
- [math]\displaystyle{ \ell_2=\sqrt{\left(\frac{\ell}{2}\right)^2+e^2} }[/math]
- [math]\displaystyle{ \ell_2=\frac{1}{2}\sqrt{ \ell^2 +4\left(r-\frac{1}{2} \sqrt{4r^2-\ell^2}\right)^2} }[/math]
Let [math]\displaystyle{ l_3 }[/math] denotes the length of a side of hexadecagon
- [math]\displaystyle{ \ell_3=\frac{1}{2}\sqrt{ \ell_2^2 +4\left(r-\frac{1}{2}\sqrt{4r^2-\ell_2^2}\right)^2 } }[/math]
similarly
- [math]\displaystyle{ \ell_{n+1}=\frac{1}{2}\sqrt{ \ell_n^2 +4\left(r-\frac{1}{2}\sqrt{4r^2-\ell_n^2}\right)^2} }[/math]
Proceeding in this way, he at last calculated the side of a 16384-gon, multiplying it by 16384 to obtain 3141.592 for a circle with diameter = 1000 units, or
- [math]\displaystyle{ \pi =3.141592. \, }[/math]
He multiplied this number by 113 and obtained 355. From this he deduced that of the traditional values of π, that is 3, 3.14, 22/7 and 355/113, the last is the most exact.[2]
See also
References
- ↑ Yoshio Mikami, Development of Mathematics in China and Japan, Chapter 20, The Studies about the Value of π etc., pp 135–138
- ↑ Yoshio Mikami, p136
 |