Sylvester's triangle problem
Sylvester's theorem or Sylvester's formula describes a particular interpretation of the sum of three pairwise distinct vectors of equal length in the context of triangle geometry. It is also referred to as Sylvester's (triangle) problem in literature, when it is given as a problem rather than a theorem. The theorem is named after the British mathematician James Joseph Sylvester.
Theorem
Consider three pairwise distinct vectors of equal length [math]\displaystyle{ \vec{u} }[/math], [math]\displaystyle{ \vec{v} }[/math] and [math]\displaystyle{ \vec{w} }[/math] each of them acting on the same point [math]\displaystyle{ O }[/math] thus creating the points [math]\displaystyle{ A }[/math], [math]\displaystyle{ B }[/math] and [math]\displaystyle{ C }[/math]. Those points form the triangle [math]\displaystyle{ \triangle ABC }[/math] with [math]\displaystyle{ O }[/math] as the center of its circumcircle. Now let [math]\displaystyle{ H }[/math] denote the orthocenter of the triangle, then connection vector [math]\displaystyle{ \overrightarrow{OH} }[/math] is equal to the sum of the three vectors:[1][2]
- [math]\displaystyle{ \overrightarrow{OH}=\vec{u}+\vec{v}+\vec{w} }[/math]
Furthermore, since the points [math]\displaystyle{ O }[/math] and [math]\displaystyle{ H }[/math] are located on the Euler line together with the centroid [math]\displaystyle{ S }[/math] the following equation holds:[3]
- [math]\displaystyle{ \overrightarrow{OH}=3\cdot \overrightarrow{OS} }[/math]
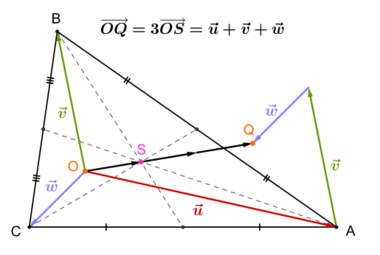
Generalisation
If the condition of equal length in Sylvester's theorem is dropped and one considers merely three arbitrary pairwise distinct vectors, then the equation above don't hold anymore. However the relation with the centroid remains true, that is:[3]
- [math]\displaystyle{ 3\cdot \overrightarrow{OS}=\vec{u}+\vec{v}+\vec{w} }[/math]
This follows directly from the definition of the centroid for a finite set of points in [math]\displaystyle{ \mathbb{R}^n }[/math], which also yields a version for [math]\displaystyle{ n }[/math] vectors acting on [math]\displaystyle{ O }[/math]:[3]
- [math]\displaystyle{ n\cdot \overrightarrow{OS}=\sum_{i=1}^n v_i }[/math]
Here [math]\displaystyle{ S }[/math] is the centroid of the vertices of the polygon generated by the [math]\displaystyle{ n }[/math] vectors acting on [math]\displaystyle{ O }[/math].[4]
References
- ↑ Roger A. Johnson: Advanced Euclidean Geometry. Dover 2007, ISBN:978-0-486-46237-0, p. 251
- ↑ Heinrich Dörrie: 100 Great Problems of Elementary Mathematics. Dover, 1965, ISBN:0486-61348-8, S. 142 (online-copy at the internet archive)
- ↑ 3.0 3.1 3.2 Michael de Villiers: "'Generalising a problem of Sylvester". In: The Mathematical Gazette, volume 96, no. 535 (March 2012), pp 78-81 (JSTOR)
- ↑ Note that the (area) centroid of a polygon with n vertices differs from the centroid of its vertices for n>3
External links
- Weisstein, Eric W.. "Sylvester's Triangle Problem". http://mathworld.wolfram.com//SylvestersTriangleProblem.html.
- Darij Grinberg: Solution to American Mathematical Monthly Problem 11398 by Stanley Huang - contains Sylvester's theorem icludings its proof as a lemma