Biology:Price equation examples

In the theory of evolution and natural selection, the Price equation expresses certain relationships between a number of statistical measures on parent and child populations. Without training in the understanding of these measures, the meaning of Price equation is rather opaque. For the less experienced person, simple and particular examples are vital to gaining an intuitive understanding of these statistical measures as they apply to populations, and the relationship between them as expressed in the Price equation.

Evolution of sight

As an example of the simple Price equation, consider a model for the evolution of sight. Suppose z_i is a real number measuring the visual acuity of an organism. An organism with a higher z_i will have better sight than one with a lower value of z_i. Let us say that the fitness of such an organism is W_i=z_i which means the more sighted it is, the fitter it is, that is, the more children it will produce. Beginning with the following description of a parent population composed of 3 types: (i = 0,1,2) with sightedness values z_i = 3,2,1:

i	0	1	2
ni	10	20	30
zi	3	2	1

Using Equation (4), the child population [math]\displaystyle{ n_i' }[/math] (assuming the character z_i doesn't change; that is, z_i = z_i')

i	0	1	2
[math]\displaystyle{ n_i' }[/math]	30	40	30
zi	3	2	1

We would like to know how much average visual acuity has increased or decreased in the population. From Equation (3), the average sightedness of the parent population is z = 5/3. The average sightedness of the child population is z' = 2, so that the change in average sightedness is:

[math]\displaystyle{ \Delta z \;\stackrel{\mathrm{def}}{=}\; z' - z = \frac{1}{3} }[/math]

which indicates that the trait of sightedness is increasing in the population. (Note that the covariance formula used below is not the standard covariance formula commonly used in mainstream textbooks. Refer to Equation (2) for Price's definition of covariance in this context.) Applying the Price equation we have (since z′_i= z_i):

[math]\displaystyle{ \Delta z = \frac{1}{w}\operatorname{cov}\left(w_i, z_i\right) = \frac{1}{3} }[/math]

Evolution of sickle cell anemia

An example of autosomal recessive inheritance. In the sickle cell case, the two parents are "carriers" who are resistant to malaria. Their children have one chance in four of inheriting both sickle cell genes and suffering sickle cell anemia, two chances in four of being a carrier themselves, and being resistant to malaria like their parents, and one chance in four of not inheriting the gene from either parent, and being susceptible to malaria.

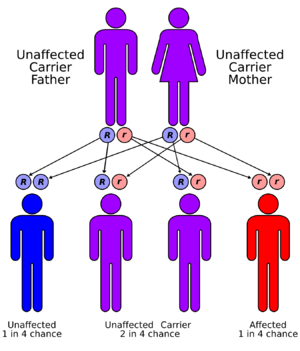
As an example of dynamical sufficiency, consider the case of sickle cell anemia. Each person has two sets of genes, one set inherited from the father, one from the mother. Sickle cell anemia is a blood disorder which occurs when a particular pair of genes both carry the 'sickle-cell trait'. The reason that the sickle-cell gene has not been eliminated from the human population by selection is because when there is only one of the pair of genes carrying the sickle-cell trait, that individual (a "carrier") is highly resistant to malaria, while a person who has neither gene carrying the sickle-cell trait will be susceptible to malaria. Let's see what the Price equation has to say about this.

Let z_i=i be the number of sickle-cell genes that organisms of type i have so that z_i = 0 or 1 or 2. Assume the population sexually reproduces and matings are random between type 0 and 1, so that the number of 0–1 matings is n₀n₁/(n₀+n₁) and the number of i–i matings is n²_i/[2(n₀+n₁)] where i = 0 or 1. Suppose also that each gene has a 1/2 chance of being passed to any given child and that the initial population is n_i=[n₀,n₁,n₂]. If b is the birth rate, then after reproduction there will be

[math]\displaystyle{ b\left(\frac{\frac{1}{2}n_0^2 + \frac{1}{2}n_0n_1 + \frac{1}{8}n_1^2}{n_0 + n_1}\right) }[/math] type 0 children (unaffected)

[math]\displaystyle{ b\left(\frac{\frac{1}{2}n_0n_1 + \frac{1}{4}n_1^2 }{n_0 + n_1}\right) }[/math] type 1 children (carriers)

[math]\displaystyle{ b\left(\frac{\frac{1}{8}n_1^2 }{n_0 + n_1}\right) }[/math] type 2 children (affected)

Suppose a fraction a of type 0 reproduce, the loss being due to malaria. Suppose all of type 1 reproduce, since they are resistant to malaria, while none of the type 2 reproduce, since they all have sickle-cell anemia. The fitness coefficients are then:

[math]\displaystyle{ \begin{align} w_0 &= ab\left(\frac{\frac{n_0^2}{2} + \frac{1}{2}n_0n_1 + \frac{1}{8}n_1^2}{n_0(n_0 + n_1)}\right) \\ w_1 &= b\left(\frac{\frac{1}{2}n_0n_1 + \frac{1}{4}n_1^2}{n_1(n_0 + n_1)} \right) \\ w_2 &= 0 \end{align} }[/math]

To find the concentration n₁ of carriers in the population at equilibrium, with the equilibrium condition of Δ z=0, the simple Price equation is used:

[math]\displaystyle{ 0 = \operatorname{cov}\left(\frac{w_i}{w}, z_i\right) = \frac{f(2 - 2a - af)}{(1 + f)(2a + 2f + af)} }[/math]

where f=n₁/n₀. At equilibrium then, assuming f is not zero:

[math]\displaystyle{ f = \frac{n_1}{n_0} = \frac{2(1 - a)}{a} }[/math]

In other words, the ratio of carriers to non-carriers will be equal to the above constant non-zero value. In the absence of malaria, a=1 and f=0 so that the sickle-cell gene is eliminated from the gene pool. For any presence of malaria, a will be smaller than unity and the sickle-cell gene will persist.

The situation has been effectively determined for the infinite (equilibrium) generation. This means that there is dynamical sufficiency with respect to the Price equation, and that there is an equation relating higher moments to lower moments. For example, for the second moments:

[math]\displaystyle{ \begin{align} \langle w_i^2z_i \rangle &= \frac{\langle w_i z_i \rangle}{z} \\ \langle w_i^2 \rangle &= \frac{ - b z^2 w^2 + 2 b z^2 w \langle w_i z_i \rangle + b z \langle w_i z_i \rangle^2 - b z^2 \langle w_i z_i \rangle^2 - 4 \langle w_i z_i \rangle^3 } {b z^2 - 4z \langle w_i z_i \rangle} \end{align} }[/math]

Sex ratios

In a 2-sex species or deme with sexes 1 and 2 where [math]\displaystyle{ z_1= 1 }[/math], [math]\displaystyle{ z_2 = 0 }[/math], [math]\displaystyle{ z }[/math] is the relative frequency of sex 1. Since all individuals have one parent of each sex, the fitness of each sex is proportional to the number of the other sex. Consider proportionality constants [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] such that [math]\displaystyle{ w_1 = a(1 - z) }[/math]and [math]\displaystyle{ w_2 = bz }[/math]. Under this scenario, a is the number of children a male would have if there he were the only male and unlimited number of females, while b is the number of children a female would have if she were the only female and unlimited number of males. This gives [math]\displaystyle{ w = (a + b)z(1 - z) }[/math] and [math]\displaystyle{ cov(w_i, z_i) + wz = E(w_i z_i) = az(1 - z) }[/math], so [math]\displaystyle{ cov(w_i, z_i) = az(1 - z) - (a + b)z^2(1 - z) = z[1 - z][a - (a + b)z] }[/math]. Hence, [math]\displaystyle{ \Delta z = \frac{a}{a + b} - z }[/math] so that [math]\displaystyle{ z' = \frac{a}{a + b} }[/math].

Under another scenario, every woman has a maximum number of children ([math]\displaystyle{ w_0=b }[/math]) so that [math]\displaystyle{ b\, n_f }[/math] children are created per generation, and every male is responsible for an equal number of children so that [math]\displaystyle{ w_1=b\, n_f/n_m }[/math] where [math]\displaystyle{ n_f }[/math] and [math]\displaystyle{ n_m }[/math] are the total number of females and males respectively. In this case, the sex ratio stabilizes at [math]\displaystyle{ z=1/2 }[/math].

Evolution of mutability

Suppose there is an environment containing two kinds of food. Let α be the amount of the first kind of food and β be the amount of the second kind. Suppose an organism has a single allele which allows it to utilize a particular food. The allele has four gene forms: A₀, A_m, B₀, and B_m. If an organism's single food gene is of the A type, then the organism can utilize A-food only, and its survival is proportional to α. Likewise, if an organism's single food gene is of the B type, then the organism can utilize B-food only, and its survival is proportional to β. A₀ and A_m are both A-alleles, but organisms with the A₀ gene produce offspring with A₀-genes only, while organisms with the A_m gene produce, among their n offspring, (n−3m) offspring with the A_m gene, and m organisms of the remaining three gene types. Likewise, B₀ and B_m are both B-alleles, but organisms with the B₀ gene produce offspring with B₀-genes only, while organisms with the B_m gene produce (n−3m) offspring with the B_m gene, and m organisms of the remaining three gene types.

Let i=0,1,2,3 be the indices associated with the A₀, A_m, B₀, and B_m genes respectively. Let w_ij be the number of viable type-j organisms produced per type-i organism. The w_ij matrix is: (with i denoting rows and j denoting columns)

[math]\displaystyle{ \mathbf{w} = \begin{bmatrix} \alpha & 0 & 0 & 0 \\ m\alpha & (n - 3m)\alpha & m\beta & m\beta \\ 0 & 0 & \beta & 0 \\ m\alpha & m\alpha & m\beta & (n - 3m)\beta \end{bmatrix} }[/math]

Mutators are at a disadvantage when the food supplies α and β are constant. They lose every generation compared to the non-mutating genes. But when the food supply varies, even though the mutators lose relative to an A or B non-mutator, they may lose less than them over the long run because, for example, an A type loses a lot when α is low. In this way, "purposeful" mutation may be selected for. This may explain the redundancy in the genetic code, in which some amino acids are encoded by more than one codon in the DNA. Although the codons produce the same amino acids, they have an effect on the mutability of the DNA, which may be selected for or against under certain conditions.

With the introduction of mutability, the question of identity versus lineage arises. Is fitness measured by the number of children an individual has, regardless of the children's genetic makeup, or is fitness the child/parent ratio of a particular genotype?. Fitness is itself a characteristic, and as a result, the Price equation will handle both.

Suppose we want to examine the evolution of mutator genes. Define the z-score as:

[math]\displaystyle{ z_i = \left[0, 1, 0, 1\right] }[/math]

in other words, 0 for non-mutator genes, 1 for mutator genes. There are two cases:

Evolution of altruism

To study the evolution of a genetic predisposition to altruism, altruism will be defined as the genetic predisposition to behavior which decreases individual fitness while increasing the average fitness of the group to which the individual belongs. First specifying a simple model, which will only require the simple Price equation. Specify a fitness w_i by a model equation:

[math]\displaystyle{ w_i = \frac{n'_i}{n_i} = k - a z_i + b z }[/math]

where z_i is a measure of altruism, the az_i term is the decrease in fitness of an individual due to altruism towards the group and bz is the increase in fitness of an individual due to the altruism of the group towards an individual. Assume that a and b are both greater than zero. From the Price equation:

[math]\displaystyle{ w\Delta z = -a\operatorname{var}\left(z_i\right) }[/math]

where var(z_i) is the variance of z_i which is just the covariance of z_i with itself:

[math]\displaystyle{ \operatorname{var}(z_i) \;\stackrel{\mathrm{def}}{=}\; \operatorname{E}(z_i^2) - \operatorname{E}(z_i)^2 }[/math]

It can be seen that, by this model, in order for altruism to persist it must be uniform throughout the group. If there are two altruist types the average altruism of the group will decrease, and the more altruistic will lose out to the less altruistic.

Now assuming a hierarchy of groups which will require the full Price equation. The population will be divided into groups, labelled with index i and then each group will have a set of subgroups labelled by index j. Individuals will thus be identified by two indices, i and j, specifying which group and subgroup they belong to. n_ij will specify the number of individuals of type ij. Let z_ij be the degree of altruism expressed by individual j of group i towards the members of group i. Let's specify the fitness w_ij by a model equation:

[math]\displaystyle{ w_{ij} = \frac{n'_{ij}}{n_{ij}} = k - a z_{ij} + b z_i }[/math]

The a z_ij term is the fitness the organism loses by being altruistic and is proportional to the degree of altruism z_ij that it expresses towards members of its own group. The b z_i term is the fitness that the organism gains from the altruism of the members of its group, and is proportional to the average altruism z_i expressed by the group towards its members. Again, in studying altruistic (rather than spiteful) behavior, it is expected that a and b are positive numbers. Note that the above behavior is altruistic only when az_ij >bz_i. Defining the group averages:

[math]\displaystyle{ \begin{align} n_i &= \sum_j n_{ij} \\ z_i &= \frac{1}{n_i}\sum_j z_{ij}n_{ij} \\ w_i &= \frac{1}{n_i}\sum_j w_{ij}n_{ij} = k + (b - a)z_i \\ n_i'&= \sum_j n_{ij}' = n_i[k + (b - a)z_i] \\ z_i'&= \frac{1}{n_i'}\sum_j z_{ij}n_{ij}' \end{align} }[/math]

and global averages:

[math]\displaystyle{ \begin{align} n &= \sum_{ij} n_{ij} = \sum_i n_i \\ z &= \frac{1}{n}\sum_{ij} z_{ij}n_{ij} = \frac{1}{n}\sum_i z_in_i \\ w &= \frac{1}{n}\sum_{ij} w_{ij}n_{ij} = \frac{1}{n}\sum_i w_in_i \\ n'&= \sum_{ij} n_{ij}' = \sum_i n_i' \\ z'&= \frac{1}{n'}\sum_{ij} z_{ij}n_{ij}' = \frac{1}{n'}\sum_i z_i'n_i' \end{align} }[/math]

It can be seen that since the z_i and z_i are now averages over a particular group, and since these groups are subject to selection, the value of Δz_i = z′_i−z_i will not necessarily be zero, and the full Price equation will be needed.

[math]\displaystyle{ \Delta z = \operatorname{cov}\left(\frac{w_i}{w}, z_i\right) + \operatorname{E}\left(w_i\,\Delta \frac{z_i}{w}\right) }[/math]

In this case, the first term isolates the advantage to each group conferred by having altruistic members. The second term isolates the loss of altruistic members from their group due to their altruistic behavior. The second term will be negative. In other words, there will be an average loss of altruism due to the in-group loss of altruists, assuming that the altruism is not uniform across the group. The first term is:

[math]\displaystyle{ \operatorname{cov}\left(\frac{w_i}{w}, z_i\right) = \left(b - a\right)\operatorname{var}(z_i) }[/math]

In other words, for b>a there may be a positive contribution to the average altruism as a result of a group growing due to its high number of altruists and this growth can offset in-group losses, especially if the variance of the in-group altruism is low. In order for this effect to be significant, there must be a spread in the average altruism of the groups.