Errors, general classification
A measurement of a physical quantity ![]() yields a random variable X, which is different from
yields a random variable X, which is different from ![]() because of various sources of measurement errors. It is useful to consider the distribution of X as caused by one single error source at a time, and to find the distribution due to all sources considered independently, convolution.
because of various sources of measurement errors. It is useful to consider the distribution of X as caused by one single error source at a time, and to find the distribution due to all sources considered independently, convolution.
The essence of experimentation consists of finding devices and methods which
- - allow one to estimate the errors reliably, and
- - keep them small enough to allow the experiment to produce meaningful conclusions.
The most important types of errors are superficially discussed in the following.
- a) Random errors occur whenever random processes are at work in a measurement, e.g. ionization in chambers, transmission of light in scintillators, conversion of a light signal into an electric signal. Being sums of many small error sources, they are usually well approximated by the normal distribution.
The effect of random errors decreases by a factor
 when the available sample size increases by a factor R.
when the available sample size increases by a factor R. - b) A special case of random error occurs when a measurement consists of counting random events. The outcome is then an integer n between 0 and a maximum number N, and the statistical distribution of n is the binomial distribution. For
 , the binomial distribution approaches the Poisson distribution. The variance of n can be estimated assuming a binomial or Poisson distribution (for the Poisson distribution, var(n)=n). Only if both n and N-n are large, is the assumption of a normal distribution for n justified (
, the binomial distribution approaches the Poisson distribution. The variance of n can be estimated assuming a binomial or Poisson distribution (for the Poisson distribution, var(n)=n). Only if both n and N-n are large, is the assumption of a normal distribution for n justified ( 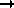 Regener51).
Regener51). c) Truncation and rounding errors occur whenever signals are converted to and processed in digital form. Comparatively easy to estimate are truncation errors occurring in digitization processes, e.g. time digitizers using a clock, mechanical digitizers of length or angle using a grating, or analogue to digital converters (ADCs) using simple divider chains. The relevant quantity in these processes is the value corresponding to the least count (e.g. the inverse clock frequency). Translating the least count (l.c.) into a statistical measure, one obtains a standard deviation of
The effect of truncation errors may be reduced by increased sample size in many cases, but they do not follow the law of Gaussian errors (
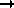 Drijard80).
Rounding errors in the processing of data, i.e. caused in algorithms by the limited word length of computers, are usually much more difficult to estimate. They depend, obviously, on parameters like word size and number representation, and even more on the numerical methods used. Rounding errors in computers may amplify harmless limitations in precision to the point of making results meaningless. A more general theoretical treatment is found in textbooks of numerical analysis (e.g. Ralston78a). In practice, algorithms suspected of producing intolerable rounding errors are submitted to stability tests with changing word length, to find a stability plateau where results are safe.
Drijard80).
Rounding errors in the processing of data, i.e. caused in algorithms by the limited word length of computers, are usually much more difficult to estimate. They depend, obviously, on parameters like word size and number representation, and even more on the numerical methods used. Rounding errors in computers may amplify harmless limitations in precision to the point of making results meaningless. A more general theoretical treatment is found in textbooks of numerical analysis (e.g. Ralston78a). In practice, algorithms suspected of producing intolerable rounding errors are submitted to stability tests with changing word length, to find a stability plateau where results are safe.d) Systematic errors are those errors which contain no randomness and can not be decreased by increasing sample size. They are due to incomplete knowledge or inadequate consideration of effects like mechanical misalignment, electronic distortion of signals, time-dependent fluctuations of experimental conditions, etc. The efforts of avoiding and detecting all possible systematic errors take the better part of design and analysis in an experiment, the general aim being that they should be compensated or understood and corrected to a level which depresses them below the level of random errors. This usually necessitates a careful scheme of calibration procedures using either special tests and data or, preferably, the interesting data themselves. A systematic error causes the expectation value of X to be different from the true value
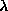 , i.e. the measurement has the bias
, i.e. the measurement has the biasOne will usually try to find some estimate b for the bias B by estimating the precision of the calibration procedures used. For lack of better knowledge one then introduces b as an additional random error (of Gaussian distribution) of
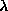 around the mean X. This is mathematically equivalent to X being normally distributed around
around the mean X. This is mathematically equivalent to X being normally distributed around 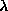 with variance b2. A systematic error is thus treated as if it were a random error, which is perfectly legitimate in the limit of many small systematic errors. However, whereas the magnitude of random errors can be estimated by comparing repeated measurements, this is not possible for systematic errors.
with variance b2. A systematic error is thus treated as if it were a random error, which is perfectly legitimate in the limit of many small systematic errors. However, whereas the magnitude of random errors can be estimated by comparing repeated measurements, this is not possible for systematic errors.- e) Gross errors are those errors originating in wrong assumptions; they result in a deterioration of results or in losses of data which are difficult to estimate in general. Despite serious preparation and careful real-time control, experiments usually produce data that require, at all levels of processing, cuts and decisions based on statistical properties and hence sometimes are taken wrongly (e.g. the limited two-track resolution of a drift chamber makes two adjacent tracks appear as one, random pulses in scintillators produce a fake trigger). The experimenter's aim is, of course, to keep the influence of gross errors below that of all other error sources. The extent of his success becomes visible when test functions are compared with their theoretical distribution. In nearly all experiments, such critical distributions exhibit tails larger than expected, which show the level of gross errors (outliers) of one sort or another.

