Neville algorithm

This algorithm is a schematic recursive way of evaluating the coefficients of a polynomial of order n-1 from n known function values

Given the n pairs (x_i,y_i), one procedes schematically:

• - first find the n ``polynomials of order zero going through the n function values at 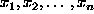, i.e. simply the yi;
• - next obtain from these the n-1 polynomials of order one going through the pairs (x_i,y_i) and (x_i+1,y_i+1);
• - next the n-2 polynomials of order two going through the triplets (x_i,y_i), (x_i+1,y_i+1) and (x_i+2,y_i+2);
• - etc.,

until one reaches the required single polynomial of order n-1 going through all points.

The recursive formula allows one to derive every polynomial from exactly two polynomials of a degree lower by one, by

The formula may be viewed as an interpolation. It translates, for instance, into a second-order polynomial defined by the equations of two straight lines by:

see Press95 for variants.