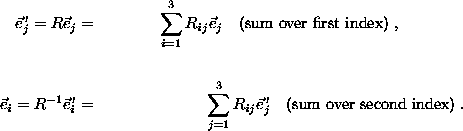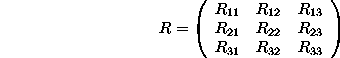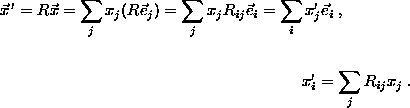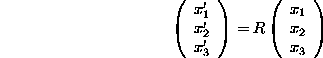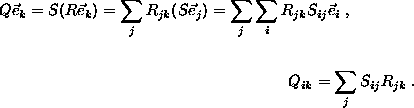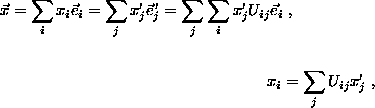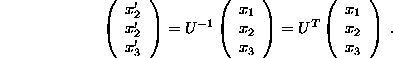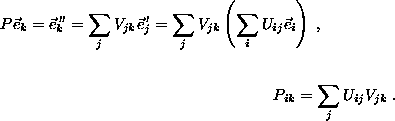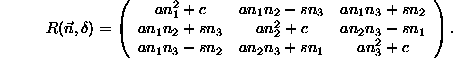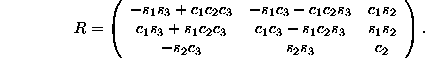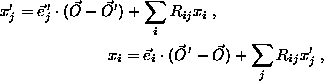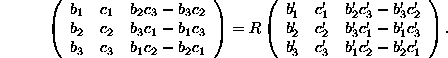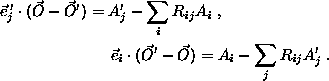Rotations
A rotation is a linear transformation (usually in three-dimensional space with a positive definite scalar product) that preserves scalar products. Usually a determinant of +1 is also postulated, else the transformation is called a reflection. If 
and 
are (three-dimensional) vectors, R is a rotation and 
and 
are the rotated vectors, then
Let 
and 
be orthonormal basis vectors, i.e. 
. Define matrix elements 
. Then
The 
matrix
which represents the rotation R, is an orthogonal matrix, since
If x1, x2, x3 are the components of the vector with respect to the basis 
,
then
In matrix notation,
where R is the matrix defined above.
If the rotation R is followed by a second rotation S, the result is a third rotation Q= SR, defined by
In terms of matrices the composition SR is simply the matrix product, since
The above formalism treats rotations as active transformations, i.e. the vectors are rotated and the basis vectors are kept fixed. The passive point of view is often adopted, where a vector is not transformed, but its coordinates x1, x2, x3 change because the basis vectors are rotated. If
then the new coordinates 
are defined by
or in matrix notation
If one passive rotation (coordinate transformation) U is followed by another, V, such that
then the total result is a third passive rotation P, such that
Note that the composition of passive rotations, first U and then V, leads to a matrix product, P=UV, in which the order is reversed. The reason for the reversal is that the matrix elements of U and of V are taken with respect to two different bases, 
and 
.
A rotation is defined by a rotation axis 
, and an angle of rotation 
. With 
the corresponding rotation matrix is
In vector notation,
A general rotation R can also be parameterized by the Euler angles 
, 
and 
, as 
, where 
is an active rotation by an angle about the axis 
. (A different convention is to use 
instead of 
, the relation is very simply that 
. The ranges of the angles are: 
, 
, 
. Explicitly, with 
, 
, 
, 
, etc., we have
Example ( 
Coordinate Systems). A Euclidean coordinate system is determined by an origin 
and three orthonormal basis vectors . Let 
be a second Euclidean coordinate system. Let x1,x2,x3 and be the coordinates of a point with respect to the two systems, i.e.
The coordinate transformations from one system to the other and back are:
where 
, i.e. R is the rotation defined by 
.
Suppose one has measured three reference points 
, 
, and 
in the two systems in order to determine the coordinate transformation. The three distances 
, 
and 
should be independent of the coordinate system; this gives three constraints
One should make a least squares fit in order to get the constraints exactly satisfied (the 
of the fit gives a consistency check of the measurements). Define 
. Then
if one defines 
. Similarly, 
. It follows that 
, and the matrix R can be found from the linear equation
The solution for R is unique whenever the vectors 
and 
are linearly independent. Finally,
 |
