Physics:Fluid thread breakup
Fluid thread breakup is the process by which a single mass of fluid breaks into several smaller fluid masses. The process is characterized by the elongation of the fluid mass forming thin, thread-like regions between larger nodules of fluid. The thread-like regions continue to thin until they break, forming individual droplets of fluid. Thread breakup occurs where two fluids or a fluid in a vacuum form a free surface with surface energy. If more surface area is present than the minimum required to contain the volume of fluid, the system has an excess of surface energy. A system not at the minimum energy state will attempt to rearrange so as to move toward the lower energy state, leading to the breakup of the fluid into smaller masses to minimize the system surface energy by reducing the surface area. The exact outcome of the thread breakup process is dependent on the surface tension, viscosity, density, and diameter of the thread undergoing breakup.
History
The examination of droplet formation has a long history, first traceable to the work of Leonardo da Vinci who wrote:[1]
"How water has tenacity in itself and cohesion between its particles. […] This is seen in the process of a drop becoming detached from the remainder, this remainder being stretched out as far as it can through the weight of the drop which is extending it; and after the drop has been severed from this mass the mass returns upwards with a movement contrary to the nature of heavy things."
He thus correctly attributed the fall of droplets to gravity and the mechanism which drives thread breakup to the cohesion of water molecules.
The first correct analysis of fluid thread breakup was determined qualitatively by Thomas Young and mathematically by Pierre-Simon Laplace between 1804 and 1805.[2][3] They correctly attributed the driver of thread breakup to surface tension properties. Moreover, they also deduced the importance of mean curvature in the creation of excess pressure in the fluid thread. Through their analysis, they showed that surface tension can behave in two ways: an elastic mechanism that can support a hanging droplet and a pressure mechanism due to capillary pressure that promotes thread breakup.
In the 1820s, the Italian physicist and hydraulic engineer Giorgio Bidone studied the deformation of jets of water issuing from orifices of various shapes.[4] Félix Savart followed in 1833 with experimental work, utilizing the stroboscopic technique to quantitatively measure thread breakup.[5] He noted that breakup is a spontaneous process, occurring without an external stimuli. This work allowed him to determine that droplets are produced from a jet flowing from a tank at a distinct rate inversely proportional to the nozzle radius and proportional to pressure in the tank. These observations facilitated Joseph Plateau's work that established the relationship between jet breakup and surface energy.[6] Plateau was able to determine the most unstable disturbance wavelength on the fluid thread, which was later revised by Lord Rayleigh to account for jet dynamics.
As the surface disturbance becomes large, non-linear theory must be applied. The behavior of jets with large disturbances was examined experimentally by Magnus and Lenard.[7][8] Their experiments helped to characterize satellite droplets, droplets that are produced in addition to the large main droplet, through the introduction of high speed photography. High speed photography is now the standard method for experimentally analyzing thread breakup.
With the advent of greater computational power, numerical simulations have begun to replace experimental efforts as the chief means of understanding fluid breakup. However, difficulty remains in accurately tracking the free surface of many liquids due to its complex behavior. The most success has occurred with fluids of low and high viscosity where the boundary integral method can be employed as the Green's function for both cases is known. Dommermuth and Yue characterized irrotational, inviscid flow by this method as did Schulkes.[9][10] Youngren and Acrivos considered the behavior of a bubble in a high viscosity liquid.[11] Stone and Leal expanded this initial work to consider the dynamics of individual drops.[12] For fluids of middling viscosity, full simulations using the Navier-Stokes equations are required with methods determining the free surface such as level-set and volume of fluid. The earliest work with full Navier-Stokes simulations was done by Fromm which focused on inkjet technology.[13] Such simulations remain an active area of research.
Physical mechanism of thread breakup
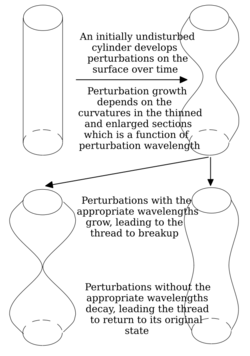
The breakup process in a fluid thread or jet begins with the development of small perturbations on the free surface of the fluid. This is known as the linear theory of fluid thread breakup. These perturbations are always present and can be generated by numerous sources including vibrations of the fluid container or non-uniformity in the shear stress on the free surface. In general, these disturbances take an arbitrary form and are thus difficult to consider rigorously. It is therefore helpful to take a Fourier transform of the disturbances to decompose the arbitrary disturbances into perturbations of various single wavelengths on the surface of the thread. In doing so, this allows one to determine which wavelengths of the disturbance will grow and which will decay in time.[14]
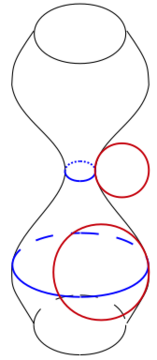
The growth and decay of wavelengths can be determined by examining the change in pressure a perturbation wavelength imposes on the interior of the fluid thread. Changes to the internal pressure of the thread are induced by capillary pressure as the free surface of the thread deforms. Capillary pressure is a function of the mean curvature of the interface at a given location at the surface, meaning the pressure is dependent on the two radii of curvature that give the shape of the surface. Within the thinned area of a fluid thread undergoing breakup, the first radius of curvature is smaller than the radius of curvature in the thickened area, leading to a pressure gradient that would tend to force liquid from the thinned to thickened areas. However, the second radius of curvature remains important to the breakup process. For some perturbation wavelengths, the effect of the second radius of curvature can overcome the pressure effect of the first radius of curvature, inducing a larger pressure in the thickened regions than the thinned regions. This would push fluid back toward the thinned regions and tend to return the thread to its original, undisturbed shape. However, for other perturbation wavelengths, the capillary pressure induced by the second radius of curvature will reinforce that of the first radius of curvature. This will drive fluid from the thinned to the thickened regions and further promote thread breakup.
The wavelength of the perturbation is therefore the critical parameter in determining whether a given fluid thread will breakup into smaller masses of fluid. Rigorous mathematical examination of the perturbation wavelengths can lead to a relation showing which wavelengths are stable for a given thread as well as which perturbation wavelengths will grow most rapidly. The size of the fluid masses resulting from the breakup of a fluid thread can be approximated by the wavelengths of the perturbation that grow most rapidly.
Non-linear behavior
While linear theory is useful in considering the growth of small disturbances on the free surface, when the disturbances grow to have a significant amplitude, non-linear effects begin to dominate breakup behavior. The non-linear behavior of the thread governs its final breakup and ultimately determines the final shape and number of the resulting fluid masses.
Nonlinearity is captured through the use of self-similarity. Self-similarity assumes that the behavior of the fluid thread as the radius approaches zero is the same as the behavior of the fluid thread when it has some finite radius. Detailed understanding of non-linear thread behavior requires the use of asymptotic expansions to generate the appropriate scaling behavior. Numerous solutions have been found for the non-linear behavior of fluid threads based on the forces that are relevant in particular circumstances.[15][16][17]
Important parameters
How a fluid thread or jet undergoes breakup is governed by several parameters among which are the Reynolds number, the Weber number, Ohnesorge number, and the disturbance wavelength. While these numbers are common in fluid mechanics, the parameters selected as scales must be appropriate to thread breakup. The length scale most often selected is the radius of the fluid thread, while the velocity is most often taken to be the velocity of the bulk fluid motion. However, these scales can change based on the characteristics of the considered problem.
The Reynolds number is the ratio between inertia and viscous effects within the thread. For large Reynolds numbers, the effects of motion of the thread are much greater than viscous dissipation. Viscosity only has a minimal damping effect on the thread. For small Reynolds numbers, viscous dissipation is large and any disturbances are rapidly damped from the thread.
The Weber number is the ratio between inertia and surface tension effects within the thread. When the Weber number is large, the inertia of the thread is large which resists the tendency of surface tension to flatten bent surfaces. For small Weber numbers, the changes in the capillary pressure due to the surface disturbances is large and surface tension dominates thread behavior.
The Ohnesorge number is the ratio between viscous and surface tension effects within the thread. As it eliminates the effects of inertia and the need for a velocity scale, it is oftentimes more convenient to express scaling relationships in terms of the Ohnesorge number rather than the Reynolds and Weber number individually.
The perturbation wavelength is the characteristic length of the disturbance on the surface of the jet, assuming that any arbitrary disturbance can be decomposed via a Fourier transform into its constitutive components. The wavelength of the perturbation is critical in determining if a particular disturbance will grow or decay in time.
Special cases
Linear stability of inviscid liquids
The linear stability of low viscosity liquids was first derived by Plateau in 1873.[14] However, his solution has become known as the Rayleigh-Plateau instability due to the extension of the theory by Lord Rayleigh to include fluids with viscosity. Rayleigh-Plateau instability is often used as an introductory case to hydrodynamic stability as well as perturbation analysis.
Plateau considered the stability of a thread of fluid when only inertial and surface tension effects were present. By decomposing an arbitrary disturbance on the free surface into its constitutive harmonics/wavelengths, he was able to derive the a condition for the stability of the jet in terms of the perturbation:
- [math]\displaystyle{ \omega^2 = \frac{\sigma k}{\rho a^2} \frac{I_1(ka)}{I_0(ka)} \left ( 1 - k^2 a^2 \right ), }[/math]
where ω is the growth rate of the perturbation, σ is the surface tension of the fluids, k is the wavenumber of perturbation, ρ is the fluid density, a is the initial radius of the unperturbed fluid, and I is the modified Bessel function of the first kind. By computing the growth rate as a function of wavenumber, one can determine that the fastest growing disturbance wavelength occurs at:
- [math]\displaystyle{ \lambda_\text{max} \approx 9.02a. }[/math]
The wavelength of maximum instability increases as the radius of the fluid thread increases. As importantly, unstable modes are only possible when:
- [math]\displaystyle{ ka \lt 1. }[/math]
Linear stability of viscous liquids
Reynolds and later Tomotika extended Plateau's work to consider the linear stability of viscous threads. Rayleigh solved for the stability of a viscous thread of viscosity [math]\displaystyle{ \mu_A }[/math] without the presence of an external fluid.[18] Tomokita solved for the stability of a fluid thread in the presence of an external fluid with its own viscosity [math]\displaystyle{ \mu_B }[/math].[19] He considered three cases where the viscosity of the fluid thread was much greater than the external environment, the viscosity of the external environment was much greater than the fluid thread, and the general case where the liquids are of arbitrary viscosity.
Fluid thread highly viscous
For the limiting case where the fluid thread is much more viscous than the external environment, the viscosity of the external environment falls from the growth rate completely. The growth rate thus becomes only a function of the initial radius of thread, the perturbation wavelength, the surface tension of the thread, and the thread viscosity.
- [math]\displaystyle{ \omega = \frac{\sigma \left ( k^2 a^2-1 \right )}{2a \mu_A} \frac{1}{k^2 a^2 + 1 - k^2 a^2 I_0^2(ka) / I_1^2(ka)} }[/math]
Plotting this, one finds that the longest wavelengths are the most unstable. As importantly, one can note that the viscosity of the fluid thread does not influence which wavelengths will be stable. Viscosity only acts to decrease how rapidly a given perturbation will grow or decay with time.
Examples of when this case would apply are when almost any liquid undergoes thread/jet breakup in an air environment.
External fluid highly viscous
For the limiting case where the external environment of the fluid thread is much more viscous than the thread itself, the viscosity of the fluid thread falls from the perturbation growth rate completely. The growth rate thus becomes only a function of the initial radius of the thread, the perturbation wavelength, the surface tension of the thread, the viscosity of the external environment, and the second order Bessel functions of the second kind.
- [math]\displaystyle{ \omega = \frac{\sigma \left (1 - k^2 a^2 \right )}{2a \mu_B} \frac{1}{k^2 a^2 + 1 - k^2 a^2 K_0^2(ka) / K_1^2(ka)} }[/math]
If one were to plot the growth rate as a function of the perturbation wavelength, one would find that the most unstable wavelengths again occur at the longest wavelengths and that the viscosity of the external environment would only act to decrease how rapidly a perturbation would grow or decay in time.
Examples of when this case would apply are when gas bubbles enter a liquid or when water falls into honey.
General case - arbitrary viscosity ratio
The general case for two viscous fluids is much more difficult to solve directly. Tomotika expressed his solution as:
- [math]\displaystyle{ \omega = \frac{\sigma \left ( 1 - k^2 a^2 \right ) }{2a \mu_B} \Phi(ka) }[/math]
where [math]\displaystyle{ \Phi }[/math] was defined as:
- [math]\displaystyle{ \begin{align} \Phi(ka) ={} &\frac{N(ka)}{D(ka)} \\ N(ka) ={} &I_1 (ka) \Delta_1 - \{ka I_0 (ka) - I_1 (ka)\} \Delta_2 \\ D (ka) ={} &\frac{\mu_A}{\mu_B} \{ka I_0 (ka) - I_1 (ka)\} \Delta_1 - \frac{\mu_A}{\mu_B} \left \{\left (k^2a^2 +1 \right ) I_1(ka) - ka I_0(ka) \right \} \Delta_2 \\ &- \{kaK_0 (ka) + K_1(ka)\} \Delta_3 - \left \{ \left ( k^2 a^2 +1 \right ) K_1 (ka) + ka K_0 (ka) \right \} \Delta_4 \end{align} }[/math]
The [math]\displaystyle{ \Delta }[/math] coefficients are most easily expressed as the determinants of the following matrices:
- [math]\displaystyle{ \begin{align} \Delta_1 &= \begin{vmatrix} kaI_0 (ka) - I_1(ka) & K_1(ka) & -kaK_0(ka) - K_1(ka) \\ I_0(ka) + kaI_1(ka) & -K_0(ka) & -K_0(ka) + kaK_1(ka) \\ \frac{\mu_A}{\mu_B}kaI_0 (ka) & K_1(ka) & -kaK_0(ka) \end{vmatrix} \\[3pt] \Delta_2 &= \begin{vmatrix} I_1(ka) & K_1(ka) & -kaK_0 (ka) - K_1(ka) \\ I_0(ka) & - K_0(ka) & -K_0(ka) + ka K_1(ka) \\ \frac{\mu_A}{\mu_B}I_1(ka) & K_1(ka) & -kaK_0(ka) \end{vmatrix} \\[3pt] \Delta_3 &= \begin{vmatrix} I_1(ka) & ka I_0(ka) - I_1(ka) & -ka K_0(ka) - K_1(ka) \\ I_0(ka) & I_0(ka) + kaI_1(ka) & -K_0(ka) + ka K_1(ka) \\ \frac{\mu_A}{\mu_B} I_1(ka) & \frac{\mu_A}{\mu_B}kaI_0(ka) & -ka K_0(ka) \end{vmatrix} \\[3pt] \Delta_4 &= \begin{vmatrix} I_1(ka) & ka I_0(ka) - I_1(ka) & K_1(ka) \\ I_0(ka) & I_0(ka) + kaI_1(ka) & -K_0(ka) \\ \frac{\mu_A}{\mu_B}I_1 (ka) & \frac{\mu_a}{\mu_B} ka I_0(ka) & K_1(ka) \end{vmatrix} \end{align} }[/math]
The resulting solution remains a function of both the thread and external environment viscosities as well as the perturbation wavelength. The most unstable combination of viscosities and perturbation occurs when [math]\displaystyle{ \mu_A/\mu_B \approx 0.28 }[/math] with [math]\displaystyle{ \lambda \approx 10.66a }[/math].
For most applications, use of the general case is unnecessary as the two fluids in question have significantly different viscosities which permits the use of one of the limiting cases. However, some instances such as the mixing of oils or oils and water may require the use of the general case.
Satellite drop formation
Satellite drops, also known as secondary droplets, are the drops produced during the thread breakup process in addition to the large main droplet. The drops result when the filament by which the main droplet in hanging from the larger fluid mass itself breaks off from the fluid mass. The fluid contained in the filament can stay as a single mass or breakup due to the recoil disturbances imposed on it by the separation of the main droplet. While the production of satellite droplets can be predicted based on fluid properties, their precise location and volume cannot be predicted.[20][21]
In general, secondary droplets are an unwanted phenomenon, especially in applications where precise deposition of droplets is important. The production of satellite droplets is governed by the non-linear dynamics of the problem near the final stages of thread breakup.
Examples
Numerous examples of the breakup of fluid threads exist in daily life. It is one of the most common fluid mechanics phenomena one experiences and as such most give the process little thought.
Flow from a faucet
Dripping water is an everyday occurrence. As water leaves the faucet, the filament attached to the faucet begins to neck down, eventually to the point that the main droplet detaches from the surface.[22] The filament cannot retract sufficiently rapidly to the faucet to prevent breakup and thus disintegrates into several small satellite drops.[22]
Air bubbles
Air bubbles are another common breakup phenomenon. As air enters a tank of liquid, like a fish tank, the thread again necks at the base to produce a bubble. Blowing bubbles from a straw into a glass behaves in much the same manner.
Pitch drop experiment
The pitch drop experiment is a famous fluid breakup experiment using high viscous tar pitch. The rate of breakup is slowed to such a degree that only 11 drops have fallen since 1927.
Drops of honey
Honey is sufficiently viscous that the surface perturbations that lead to breakup are almost fully damped from honey threads. This results in the production of long filaments of honey rather than individual droplets.
References
- ↑ da Vinci, Leonardo (1958). MacCurdy,Edward. ed. The Notebooks of Leonardo da Vinci. 2. New York, New York, USA: George Braziller. p. 748. https://archive.org/details/notebooksofleona027479mbp.
- ↑ de Laplace, P.S. (1805). Mechanique Celeste Supplement au X Libre. Paris: Courier.
- ↑ Young, T (1805). "An Essay on the Cohesion of Fluids". Philosophical Transactions of the Royal Society of London 95: 65–87. doi:10.1098/rstl.1805.0005.
- ↑ See:
- Bidone, George (1822) (in French). Expériences sur divers cas de la contraction de la veine fluide, et remarque sur la manière d'avoir égard à la contraction dans le calcul de la dépense des orifices. Turin, (Italy): Imprimerie Royale. https://archive.org/details/TO0E040773_TO0324_PNI-2250_000004.
- Bidone, George (1830). "Expériences sur la forme et sur la direction des veines et des courants d'eau lancés par diverses ouvertures" (in French). Memorie della Reale Accademia delle Scienze di Torino 34: 229–363. https://www.biodiversitylibrary.org/item/32656#page/295/mode/1up.
- ↑ Savart, Félix (1833). "Mémoire sur la constitution des veines liquides lancées par des orifices circulaires en mince paroi" (in French). Annales de chimie et de physique. 2nd series 53: 337–386. https://babel.hathitrust.org/cgi/pt?id=ien.35556000270512&view=1up&seq=339.
- ↑ Plateau, J. (1850). "Ueber die Gränze der Stabilität eines flüssigen Cylinders" (in German). Annalen der Physik und Chemie. 2nd series 80 (8): 566–569. doi:10.1002/andp.18501560808. Bibcode: 1850AnP...156..566P. https://babel.hathitrust.org/cgi/pt?id=uc1.b4433618&view=1up&seq=584.
- ↑ Magnus, G. (1859). "Hydraulische Untersuchungen; zweiter Theil" (in German). Annalen der Physik und Chemie. 2nd series 106 (1): 1–32. doi:10.1002/andp.18591820102. Bibcode: 1859AnP...182....1M. https://zenodo.org/record/1423662.
- ↑ Lenard, Philipp (1887). "Ueber die Schwingungen fallender Tropfen" (in German). Annalen der Physik und Chemie. 3rd series 30 (2): 209–243. doi:10.1002/andp.18872660202. Bibcode: 1887AnP...266..209L. https://babel.hathitrust.org/cgi/pt?id=wu.89048352645&view=1up&seq=231.
- ↑ Dommermuth, DG; Yue DKP (1987). "Numerical simulations of nonlinear axisymmetric flows with a free surface". Journal of Fluid Mechanics 178: 195–219. doi:10.1017/s0022112087001186. Bibcode: 1987JFM...178..195D.
- ↑ Schulkes, RMS (1994). "The evolution of capillary fountains". Journal of Fluid Mechanics 261: 223–252. doi:10.1017/s0022112094000327. Bibcode: 1994JFM...261..223S.
- ↑ Youngren, GK; Acrivos A (1975). "Stokes flow past a particle of arbitrary shape: a numerical method of solution". Journal of Fluid Mechanics 69 (2): 377–403. doi:10.1017/s0022112075001486. Bibcode: 1975JFM....69..377Y.
- ↑ Stone, HA; Leal LG (1989). "Relaxation and breakup of an initially extended drop in an otherwise quiescent fluid". Journal of Fluid Mechanics 198: 399. doi:10.1017/s0022112089000194. Bibcode: 1989JFM...198..399S. https://authors.library.caltech.edu/31527/1/STOjfm89.pdf.
- ↑ Fromm, JE (1984). "Numerical Calculation of the Fluid Dynamics of Drop-on-Demand Jets". IBM Journal of Research and Development 28 (3): 322–333. doi:10.1147/rd.283.0322.
- ↑ 14.0 14.1 Plateau, J (1850). "Ueber die Gränze der Stabilität eines flüssigen Cylinders". Annalen der Physik 80 (8): 566–569. doi:10.1002/andp.18501560808. Bibcode: 1850AnP...156..566P. https://zenodo.org/record/1423622.
- ↑ Ting, L; Keller JB (1990). "Slender Jets and Thin Sheets with Surface Tension". SIAM Journal on Applied Mathematics 50 (6): 1533–1546. doi:10.1137/0150090.
- ↑ Papageorgiou, DT (1995). "On the breakup of viscous liquid threads". Physics of Fluids 7 (7): 1529–1544. doi:10.1063/1.868540. Bibcode: 1995PhFl....7.1529P.
- ↑ Lister, JR; Stone HA (1998). "Capillary breakup of a viscous thread surrounded by another viscous fluid". Physics of Fluids 10 (11): 2758–2764. doi:10.1063/1.869799. Bibcode: 1998PhFl...10.2758L.
- ↑ Rayleigh, Lord (1892). "XVI. On the instability of a cylinder of viscous liquid under capillary force". Philosophical Magazine 34 (207): 145–154. doi:10.1080/14786449208620301. https://zenodo.org/record/1431201.
- ↑ Tomotika, S (1935). "On the Instability of a Cylindrical Thread of a Viscous Liquid Surrounded by Another Viscous Fluid". Proceedings of the Royal Society of London A 150 (870): 322–337. doi:10.1098/rspa.1935.0104. Bibcode: 1935RSPSA.150..322T.
- ↑ Singh, Gaurav. "Satellite Drop Formation". http://myopticaltrek.wordpress.com/water_photograhy/satellite-drops/. Retrieved 18 November 2013.
- ↑ Henderson, D; Pritchard W; Smolka Linda (1997). "On the pinch-off of a pendant drop of viscous fluid". Physics of Fluids 9 (11): 3188. doi:10.1063/1.869435. Bibcode: 1997PhFl....9.3188H.
- ↑ 22.0 22.1 "Liquid Jet Breakup" (in en). 2012-12-12. https://myopticaltrek.wordpress.com/water-dripping-from-faucet/.