Extremal graph theory
Extremal graph theory is a branch of combinatorics, itself an area of mathematics, that lies at the intersection of extremal combinatorics and graph theory. In essence, extremal graph theory studies how global properties of a graph influence local substructure. [1] Results in extremal graph theory deal with quantitative connections between various graph properties, both global (such as the number of vertices and edges) and local (such as the existence of specific subgraphs), and problems in extremal graph theory can often be formulated as optimization problems: how big or small a parameter of a graph can be, given some constraints that the graph has to satisfy? [2] A graph that is an optimal solution to such an optimization problem is called an extremal graph, and extremal graphs are important objects of study in extremal graph theory.
Extremal graph theory is closely related to fields such as Ramsey theory, spectral graph theory, computational complexity theory, and additive combinatorics, and frequently employs the probabilistic method.
History
Bollobás (2004) [3]
Mantel's Theorem (1907) and Turán's Theorem (1941) were some of the first milestones in the study of extremal graph theory. [4] In particular, Turán's theorem would later on become a motivation for the finding of results such as the Erdős–Stone theorem (1946).[1] This result is surprising because it connects the chromatic number with the maximal number of edges in an [math]\displaystyle{ H }[/math]-free graph. An alternative proof of Erdős–Stone was given in 1975, and utilised the Szemerédi regularity lemma, an essential technique in the resolution of extremal graph theory problems.[4]
Topics and concepts
Graph coloring
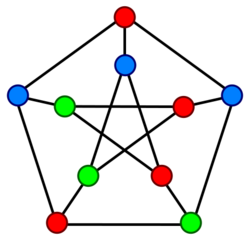
A proper (vertex) coloring of a graph [math]\displaystyle{ G }[/math] is a coloring of the vertices of [math]\displaystyle{ G }[/math] such that no two adjacent vertices have the same color. The minimum number of colors needed to properly color [math]\displaystyle{ G }[/math] is called the chromatic number of [math]\displaystyle{ G }[/math], denoted [math]\displaystyle{ \chi(G) }[/math]. Determining the chromatic number of specific graphs is a fundamental question in extremal graph theory, because many problems in the area and related areas can be formulated in terms of graph coloring.[2]
Two simple lower bounds to the chromatic number of a graph [math]\displaystyle{ G }[/math] is given by the clique number [math]\displaystyle{ \omega(G) }[/math]—all vertices of a clique must have distinct colors—and by [math]\displaystyle{ |V(G)|/\alpha(G) }[/math], where [math]\displaystyle{ \alpha(G) }[/math] is the independence number, because the set of vertices with a given color must form an independent set.
A greedy coloring gives the upper bound [math]\displaystyle{ \chi(G) \le \Delta(G) + 1 }[/math], where [math]\displaystyle{ \Delta(G) }[/math] is the maximum degree of [math]\displaystyle{ G }[/math]. When [math]\displaystyle{ G }[/math] is not an odd cycle or a clique, Brooks' theorem states that the upper bound can be reduced to [math]\displaystyle{ \Delta(G) }[/math]. When [math]\displaystyle{ G }[/math] is a planar graph, the four-color theorem states that [math]\displaystyle{ G }[/math] has chromatic number at most four.
In general, determining whether a given graph has a coloring with a prescribed number of colors is known to be NP-hard.
In addition to vertex coloring, other types of coloring are also studied, such as edge colorings. The chromatic index [math]\displaystyle{ \chi'(G) }[/math] of a graph [math]\displaystyle{ G }[/math] is the minimum number of colors in a proper edge-coloring of a graph, and Vizing's theorem states that the chromatic index of a graph [math]\displaystyle{ G }[/math] is either [math]\displaystyle{ \Delta(G) }[/math] or [math]\displaystyle{ \Delta(G)+1 }[/math].
Forbidden subgraphs
The forbidden subgraph problem is one of the central problems in extremal graph theory. Given a graph [math]\displaystyle{ G }[/math], the forbidden subgraph problem asks for the maximal number of edges [math]\displaystyle{ \operatorname{ex}(n,G) }[/math] in an [math]\displaystyle{ n }[/math]-vertex graph that does not contain a subgraph isomorphic to [math]\displaystyle{ G }[/math].
When [math]\displaystyle{ G = K_r }[/math] is a complete graph, Turán's theorem gives an exact value for [math]\displaystyle{ \operatorname{ex}(n,K_r) }[/math] and characterizes all graphs attaining this maximum; such graphs are known as Turán graphs. For non-bipartite graphs [math]\displaystyle{ G }[/math], the Erdős–Stone theorem gives an asymptotic value of [math]\displaystyle{ \operatorname{ex}(n, G) }[/math] in terms of the chromatic number of [math]\displaystyle{ G }[/math]. The problem of determining the asymptotics of [math]\displaystyle{ \operatorname{ex}(n, G) }[/math] when [math]\displaystyle{ G }[/math] is a bipartite graph is open; when [math]\displaystyle{ G }[/math] is a complete bipartite graph, this is known as the Zarankiewicz problem.
Homomorphism density
The homomorphism density [math]\displaystyle{ t(H, G) }[/math] of a graph [math]\displaystyle{ H }[/math] in a graph [math]\displaystyle{ G }[/math] describes the probability that a randomly chosen map from the vertex set of [math]\displaystyle{ H }[/math] to the vertex set of [math]\displaystyle{ G }[/math] is also a graph homomorphism. It is closely related to the subgraph density, which describes how often a graph [math]\displaystyle{ H }[/math] is found as a subgraph of [math]\displaystyle{ G }[/math].
The forbidden subgraph problem can be restated as maximizing the edge density of a graph with [math]\displaystyle{ G }[/math]-density zero, and this naturally leads to generalization in the form of graph homomorphism inequalities, which are inequalities relating [math]\displaystyle{ t(H, G) }[/math] for various graphs [math]\displaystyle{ H }[/math]. By extending the homomorphism density to graphons, which are objects that arise as a limit of dense graphs, the graph homomorphism density can be written in the form of integrals, and inequalities such as the Cauchy-Schwarz inequality and Hölder's inequality can be used to derive homomorphism inequalities.
A major open problem relating homomorphism densities is Sidorenko's conjecture, which states a tight lower bound on the homomorphism density of a bipartite graph in a graph [math]\displaystyle{ G }[/math] in terms of the edge density of [math]\displaystyle{ G }[/math].
Graph regularity
Szemerédi's regularity lemma states that all graphs are 'regular' in the following sense: the vertex set of any given graph can be partitioned into a bounded number of parts such that the bipartite graph between most pairs of parts behave like random bipartite graphs.[2] This partition gives a structural approximation to the original graph, which reveals information about the properties of the original graph.
The regularity lemma is a central result in extremal graph theory, and also has numerous applications in the adjacent fields of additive combinatorics and computational complexity theory. In addition to (Szemerédi) regularity, closely related notions of graph regularity such as strong regularity and Frieze-Kannan weak regularity have also been studied, as well as extensions of regularity to hypergraphs.
Applications of graph regularity often utilize forms of counting lemmas and removal lemmas. In simplest forms, the graph counting lemma uses regularity between pairs of parts in a regular partition to approximate the number of subgraphs, and the graph removal lemma states that given a graph with few copies of a given subgraph, we can remove a small number of edges to eliminate all copies of the subgraph.
See also
Related fields
- Ramsey theory
- Ramsey-Turán theory
- Spectral graph theory
- Additive combinatorics
- Computational complexity theory
- Probabilistic combinatorics
Techniques and methods
Theorems and conjectures (in addition to ones mentioned above)
References
- ↑ 1.0 1.1 Diestel, Reinhard (2010), Graph Theory (4th ed.), Berlin, New York: Springer-Verlag, pp. 169–198, ISBN 978-3-642-14278-9, http://diestel-graph-theory.com/index.html/, retrieved 2013-11-18
- ↑ 2.0 2.1 2.2 Template:Princeton Companion to Mathematics
- ↑ Bollobás, Béla (2004), Extremal Graph Theory, New York: Dover Publications, ISBN 978-0-486-43596-1
- ↑ 4.0 4.1 Bollobás, Béla (1998), Modern Graph Theory, Berlin, New York: Springer-Verlag, pp. 103–144, ISBN 978-0-387-98491-9
 |