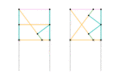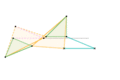Physics:Straight line mechanism

From HandWiki
Revision as of 22:51, 5 March 2023 by MainAI6 (talk | contribs) (url)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Short description: Mechanisms generating real or approximate straight line motion


Roberts Linkage.
Links of the same color are the same length.
Sarrus Linkage.
Parts of the same color are the same dimensions.
Peaucellier-Lipkin Inversor.
Links of the same color are the same length.

A straight line mechanism is a mechanism that produces a perfect or approximate straight line. The first mechanism known to produce straight line motion was an approximation, described in 1784 by James Watt.

They are used in a variety of applications, such as engines, vehicle suspensions, walking robots, and rover wheels.[citation needed]

History

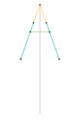
In the late eighteenth century, before the development of the planer and the milling machine, it was extremely difficult to machine straight, flat surfaces. During that era, much thought was given to the problem of attaining a straight-line motion, as this would allow the flat surfaces to be machined. To find a solution to the problem, the first straight line mechanism was developed by James Watt, for guiding the piston of early steam engines. Although it does not generate an exact straight line, a good approximation is achieved over a considerable distance of travel.

Perfect straight line linkages were later discovered in the nineteenth century, but they weren't as needed, as by then other techniques for machining had been developed.[citation needed]

List of linkages

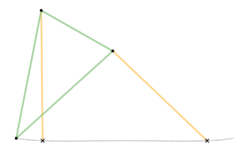
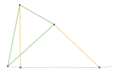
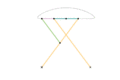
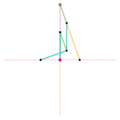
Approximate straight line linkages

These mechanisms often utilize four bar linkages as they require very few pieces. These four-bar linkages have coupler curves that have one or more regions of approximately perfect straight line motion. The exception in this list is Watt's parallel motion, which combines Watt's linkage with another four-bar linkage – the pantograph – to amplify the existing approximate straight line movement.

It is not possible to create perfectly straight line motion using a four-bar linkage, without using a prismatic joint.

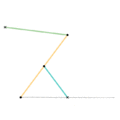
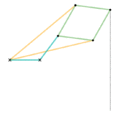
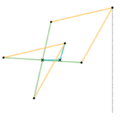
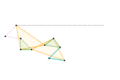
Perfect straight line linkages

Eventually, perfect straight line motion would be achieved.

The Sarrus linkage was the first perfect linear linkage, made in 1853. However, it is a spatial linkage rather than a planar linkage. The first planar linkage would not be made until 1864.

Currently, all planar linkages which produce perfect linear motion utilize the inversion around a circle to produce a hypothetical circle of infinite radius, which is a line. This is why they are called inversors or inversor cells.
The simplest solutions are Hart's W-frame – which use 6-bars – and the Quadruplanar inversors – Sylvester-Kempe and Kumara-Kampling, which also use 6-bars.

The Scott Russell linkage (1803) translates linear motion through a right angle, but is not a straight line mechanism in itself. The Grasshopper beam/Evans linkage, an approximate straight line linkage, and the Bricard linkage, an exact straight line linkage, share similarities with the Scott Russell linkage and the Trammel of Archimedes.

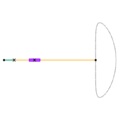
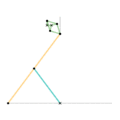
Compound eccentric mechanisms with elliptical motion

These mechanisms use the principle of a rolling curve instead of a coupler curve and can convert continuous, rather than just limited, rotary motion to reciprocating motion and vice versa via elliptical motion. The straight-line sinusoidal motion produces no second-order inertial forces, which simplifies balancing in high-speed machines.

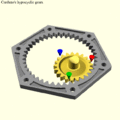
  • Cardan straight line mechanism. Using the principle of the Tusi couple (1247), a spur gear rolls inside an internally toothed ring gear of twice the diameter. The hypocycloid traced by any point on the pitch circle of the smaller gear is a diameter of the larger gear. The mechanism has been used in Murray's Hypocyclic Engine.
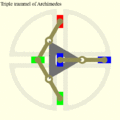
  • Trammel of Archimedes. Originally an ellipsograph. As a mechanism, it uses the fact that a circle and a straight line are special cases of an ellipse. It is based on much the same kinematic principle as Cardan's straight line mechanism (above) and could be considered as a spur gear with two teeth in a ring gear with four teeth. It has been used in the Baker-Cross engine.[3] It has been used in inverted form in Parsons' steam engine[4] and can still be found today in a similar form in the Oldham coupling.
  • MultiFAZE mechanism. The Multiple Fixed Axis Shaft Compound Eccentric mechanism also uses elliptical motion, but here the axes of the contrarotating parts are separated laterally, and the drive between them is transmitted by spur gears instead of a bearing, to reduce friction and wear. A draft article exists. The mechanism has been used in the Stiller-Smith engine.[5]

Gallery

Approximate straight line linkages

Parts/links of the same color are the same dimensions.

  • Watt's linkage

  • Watts parallel motion linkage

  • Evans "Grasshopper" linkage

  • Roberts linkage

  • Chebyshev linkage

  • Chebyshev lambda linkage

  • Chebyshev table linkage

  • Hoecken's linkage

Perfect straight line linkages

Parts/links of the same color are the same dimensions.

  • Sarrus linkage (Bars variant)

  • Sarrus linkage (Plates variant)

  • Peaucellier-Lipkin inversor

  • Harts inversor 1

  • Harts inversor 2

  • Perrolatz inversor

  • Kempe kite inversor 1

  • Kempe kite inversor 2

  • Kempe kite inversor 3

  • Scott Russell linkage (slider connection)

  • Scott Russell linkage (connected to Peaucellier-Lipkin linkage)

  • Bricard inversor

  • Sylvester-Kempe quadruplanar inversor 1

  • Sylvester-Kempe quadruplanar inversor 2

  • Sylvester-Kempe quadruplanar inversor 3

  • Kumara-Kampling inversor

Compound eccentric mechanisms with elliptical motion

  • Cardan's hypocyclic gear pair: the red, green and blue pins move in straight lines.

  • Three Archimedes trammels on a triangular rotor showing the circular orbit of the trammel midpoints.

  • 60° X4 engine with MultiFAZE mechanism, fully balanced.

See also

Sources

  1. ↑ Kempe, Alfred Bray (1877) (in en). How to Draw a Straight Line: A Lecture on Linkages. Macmillan and Company. ISBN 978-1-4297-0244-7. https://books.google.com/books?id=QsF6mxz0Fl4C. 
  2. ↑ Artobolevsky, Ivan Ivanovich. Mechanisms in modern engineering design. ISBN 978-5-9710-5698-0. 
  3. ↑ Four-cylinder, Four-cycle Engine With Two Reciprocating Components, A.J.S Baker, M.E Cross, The Institution of Mechanical Engineeers, Automobile Division, Volume 188 38/74
  4. ↑ Parsons' epicyclic engine
  5. ↑ Clean engines - A combination of advanced materials and a new engine design
  • Theory of Machines and Mechanisms, Joseph Edward Shigley

External links




Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Straight_line_mechanism&oldid=2564403"