Physics:Product operator formalism

In NMR spectroscopy, the product operator formalism is a method used to determine the outcome of pulse sequences in a rigorous but straightforward way. With this method it is possible to predict how the bulk magnetization evolves with time under the action of pulses applied in different directions. It is a net improvement from the semi-classical vector model which is not able to predict many of the results in NMR spectroscopy and is a simplification of the complete density matrix formalism.

In this model, for a single spin, four base operators exist: [math]\displaystyle{ I_x }[/math], [math]\displaystyle{ I_y }[/math], [math]\displaystyle{ I_z }[/math] and [math]\displaystyle{ E/2 }[/math] which represent respectively polarization (population difference between the two spin states), single quantum coherence (magnetization on the xy plane) and the unit operator. Many other, non-classical operators exist for coupled systems. Using this approach, the evolution of the magnetization under free precession is represented by [math]\displaystyle{ I_z }[/math] and corresponds to a rotation about the z-axis with a phase angle proportional to the chemical shift of the spin in question:

[math]\displaystyle{ I_x \xrightarrow{\omega \tau I_z} \cos (\omega \tau)I_x - \sin (\omega \tau)I_y }[/math]

Pulses about the x and y axis can be represented by [math]\displaystyle{ I_x }[/math] and [math]\displaystyle{ I_y }[/math] respectively; these allow to interconvert the magnetization between planes and ultimately to observe it at the end of a sequence. Since every spin will evolve differently depending on its shift, with this formalism it is possible to calculate exactly where the magnetization will end up and hence devise pulse sequences to measure the desired signal while excluding others.

The product operator formalism is particularly useful in describing experiments in two-dimensions like COSY, HSQC and HMBC.

Motivation for sets of spin-1/2 particles

Throughout this section, the reduced Planck constant [math]\displaystyle{ \hbar = 1 }[/math] for convenience.

The product operator formalism is usually applied to sets of spin-1/2 particles, since the fact that the individual operators satisfy [math]\displaystyle{ L_x^2 = L_y^2 = L_z^2 \propto \mathbf{1} }[/math], where [math]\displaystyle{ \mathbf{1} }[/math] is the identity operator, makes the commutation relations of product operators particularly simple. In principle the formalism could be extended to higher spins, but in practice the general irreducible spherical tensor treatment is more often used. As such, we consider only the spin-1/2 case below.

The main idea of the formalism is to make it easier to follow the system density operator [math]\displaystyle{ \rho }[/math], which evolves under a Hamiltonian [math]\displaystyle{ H }[/math] according to the Liouville-von Neumann equation as

[math]\displaystyle{ \frac{\partial \rho}{\partial t} = -\mathrm{i}[H, \rho]. }[/math]

For a time-independent Hamiltonian, the density operator inherits its solutions from the Schrödinger time-evolution operator [math]\displaystyle{ U(t) = \exp(-\mathrm{i} H t) }[/math] as

[math]\displaystyle{ \rho(t) = U(t)\,\rho(0)\,U^{-1}(t) = \exp(-\mathrm{i} H t)\, \rho(0)\, \exp(+\mathrm{i} H t) }[/math]

Density operator-state duality

Suppose a single spin-1/2 [math]\displaystyle{ L }[/math] is in the state [math]\displaystyle{ |\uparrow\,\rangle }[/math], which is an eigenstate of the z-spin operator [math]\displaystyle{ L_z }[/math], that is [math]\displaystyle{ L_z|\uparrow\,\rangle = \frac{1}{2}|\uparrow\,\rangle }[/math]. Similarly [math]\displaystyle{ L_z|\downarrow\,\rangle = -\frac{1}{2}|\downarrow\,\rangle }[/math]. Making use of the expansion of a Hermitian operator [math]\displaystyle{ A }[/math] in terms of projections onto its eigenkets [math]\displaystyle{ |a\rangle }[/math] with eigenvalues [math]\displaystyle{ a }[/math] as [math]\displaystyle{ A = \sum a|a\rangle\langle a| }[/math], the associated density operator is

[math]\displaystyle{ \begin{align} \rho_{|\uparrow\,\rangle} &= |\uparrow\,\rangle\langle\,\uparrow|\\ &= \frac{1}{2}(|\uparrow\,\rangle\langle\,\uparrow| + |\downarrow\,\rangle\langle\,\downarrow|) + \frac{1}{2}(|\uparrow\,\rangle\langle\,\uparrow| - |\downarrow\,\rangle\langle\,\downarrow|)\\ &= \frac{1}{2}\mathbf{1} + L_z, \end{align} }[/math]

where [math]\displaystyle{ \mathbf{1} }[/math] is the identity operator. Similarly, the density operator for the state [math]\displaystyle{ |\downarrow\,\rangle }[/math] is

[math]\displaystyle{ \rho_{|\downarrow\,\rangle} = \frac{1}{2}\mathbf{1} - L_z }[/math]

Since the spin operators [math]\displaystyle{ L_x, L_y, L_z }[/math] are all traceless and the expectation value of an operator [math]\displaystyle{ A }[/math] for a system with density operator [math]\displaystyle{ \rho }[/math] is [math]\displaystyle{ \langle A\rangle = \operatorname{tr}(\rho A) }[/math], the terms proportional to the unit operator [math]\displaystyle{ \mathbf{1} }[/math] do not affect the expectations of the spin operators. Additionally those parts do not evolve in time, since they trivially commute with the Hamiltonian. Therefore those terms can be ignored, and the state [math]\displaystyle{ |\uparrow\,\rangle }[/math] corresponds to a density operator [math]\displaystyle{ +L_z }[/math], while the state [math]\displaystyle{ |\downarrow\,\rangle }[/math] corresponds to a density operator [math]\displaystyle{ -L_z }[/math]. In exactly the same manner, polarisation along the positive x-axis, that is a state [math]\displaystyle{ |\uparrow_x\,\rangle }[/math], corresponds to a density operator [math]\displaystyle{ +L_x }[/math]. This idea extends naturally to multiple spins, where the states and operators are direct products of single-spin states and operators. Hence operator terms in the density operator have a direct duality with states.

In the case of two spins [math]\displaystyle{ L, S }[/math], the terms in the density operator (ignoring the identity on its own) can be interpreted as representing

• [math]\displaystyle{ L_z, S_z }[/math] - longitudinal magnetisation
• [math]\displaystyle{ L_x, L_y, S_x, S_y }[/math] - in-phase transverse magnetisation, which is the observable quantity in NMR.
• [math]\displaystyle{ 2 L_x S_z, 2 L_y S_z, 2 L_z S_x, 2 L_z S_y }[/math] - anti-phase longitudinal magnetisation
• [math]\displaystyle{ 2 L_z S_z }[/math] - longitudinal two-spin order
• [math]\displaystyle{ 2 L_x S_x, 2 L_x S_y, 2 L_y S_x, 2 L_y S_y }[/math] - other coherences, which are more difficult to interpret, but may evolve into other terms

where eg [math]\displaystyle{ L_z }[/math] is a shorthand for the Kronecker product [math]\displaystyle{ L_z \otimes \mathbf{1}_S }[/math], where [math]\displaystyle{ \mathbf{1}_S }[/math] is the identity operator on the [math]\displaystyle{ S }[/math] spin, and similarly [math]\displaystyle{ L_x S_z }[/math] is a shorthand for [math]\displaystyle{ L_x \otimes S_z }[/math].

The factors of two in the 'true' two-spin operators are to allow for convenient commutation relations in this specific spin-1/2 case - see below. Note also that we could instead choose to expand the density operator in the basis [math]\displaystyle{ L_z, L_\pm = L_x \pm \mathrm{i}\, L_y }[/math] etc, where the transverse operators have been replaced with raising and lowering operators. With quadrature detection, the observable associated with an individual spin is effectively the non-Hermitian [math]\displaystyle{ L_\pm }[/math], so this is sometimes more convenient.

Evolution of the density operator

Consider operators [math]\displaystyle{ A, B, C }[/math] that obey the cyclic commutation relations

[math]\displaystyle{ \begin{align} \left.[A, B]\right. &= \mathrm{i} C,\\ \left.[B, C]\right. &= \mathrm{i} A,\\ \left.[C, A]\right. &= \mathrm{i} B. \end{align} }[/math]

In fact only the first two relations are necessary for the following derivation, but since we are usually working with operators associated with Cartesian directions, such as the individual angular momentum operators, the third commutator follows by a symmetry argument.

Introduce also the commutation superoperator [math]\displaystyle{ \hat F }[/math] of an operator [math]\displaystyle{ F }[/math] (in our case, this is more formally related to the adjoint representation of the Lie algebra whose elements are [math]\displaystyle{ A, B, C }[/math]), which acts as

[math]\displaystyle{ \hat F\, \bullet = [F, \bullet] }[/math]

In particular, for the cyclic operators, we have

[math]\displaystyle{ \begin{align} \hat B A &= [B, A] = -\mathrm{i} C,\\ {\hat B}^2 A &= [B, [B, A]] = [B, -\mathrm{i}C] = -\mathrm{i} [B, C] = A, \end{align} }[/math]

and consequently for integer [math]\displaystyle{ n \ge 0 }[/math]

[math]\displaystyle{ \begin{align} {\hat B}^{2n} A &= A,\\ {\hat B}^{2n+1} A &= -\mathrm{i} C. \end{align} }[/math]

An identity for two operators [math]\displaystyle{ F, G }[/math] is

[math]\displaystyle{ \exp(F)G\exp(-F) = \exp(\hat F) G, }[/math]

which can be derived by putting [math]\displaystyle{ F \to t F }[/math] where [math]\displaystyle{ t }[/math] is a scalar parameter, differentiating both sides with respect to [math]\displaystyle{ t }[/math], and noting that both sides satisfy the same differential equation in that parameter, with the same initial condition at [math]\displaystyle{ t=0 }[/math]. In particular, for some scalar parameter [math]\displaystyle{ \theta }[/math], we have

[math]\displaystyle{ \begin{align} \exp(-\mathrm{i}\theta B) A \exp(+\mathrm{i}\theta B) &= \exp(-\mathrm{i}\theta \hat B)A\\ &= \sum_{n=0}^\infty \frac{(-\mathrm i \theta)^n}{n!} {\hat B}^n A\\ &= \sum_{n=0}^\infty \left[\frac{(-\mathrm i \theta)^{2n}}{(2n)!}\, A + \frac{(-\mathrm i \theta)^{2n+1}}{(2n+1)!}\cdot-\mathrm{i}C\right]\\ &= A \sum_{n=0}^\infty \frac{(-1)^n}{(2n)!}\theta^{2n} - C\sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)!}\theta^{2n+1}\\ &= \cos\theta\, A - \sin\theta\, C, \end{align} }[/math]

(1)

where the final equality follows from recognising the Taylor series for sine and cosine. Now suppose that the density operator at time zero is [math]\displaystyle{ \rho(0) = A }[/math], and it is allowed to freely evolve under the Hamiltonian [math]\displaystyle{ H = \alpha\, B }[/math] where [math]\displaystyle{ \alpha }[/math] is some scalar. Using the results above, the density operator at some later time [math]\displaystyle{ t }[/math] will be given by

[math]\displaystyle{ \rho(t) = \exp(-\mathrm{i}\alpha t\, B) A \exp(+\mathrm{i}\alpha t\, B) = \cos\alpha t\, A - \sin\alpha t\, C. }[/math]

(2)

The interpretation of this is that although nuclear spin angular momentum itself is not connected to rotations in three-dimensional space in the same way that angular momentum is, the evolution of the density operator can be viewed as rotations in an abstract space, in which the operators [math]\displaystyle{ A, B, C }[/math] are the generators of rotations about the axes. An example of such a set of generators is just the spin operators [math]\displaystyle{ L_x, L_y, L_z }[/math] themselves.

We now also introduce the 'arrow notation' typically used in NMR, which writes the general evolution given above as the shorthand

[math]\displaystyle{ A \xrightarrow{\alpha\, B t} \cos\alpha t\, A - \sin\alpha t\, C }[/math].

With more specific reference to the radiofrequency pulses applied during NMR experiments, a hard pulse with tip angle [math]\displaystyle{ \theta }[/math] around a direction [math]\displaystyle{ q }[/math] is written as [math]\displaystyle{ (\theta)_q }[/math] above the arrow and corresponds to taking [math]\displaystyle{ B=L_q }[/math] as the rotation generator in Equation 1. When there is no ambiguity, the arrow label may be omitted, or be eg text instead.

Note that a more complicated calculation has now been reduced to a simpler procedure that requires no knowledge of the underlying quantum mechanics, especially since the subspaces of cyclic operators can be tabulated in advance.

Examples

The 180°-refocussing pulse

The Hamiltonian for a single spin [math]\displaystyle{ L }[/math] evolving under a chemical shift of angular frequency [math]\displaystyle{ \omega }[/math] is

[math]\displaystyle{ H = \omega L_z, }[/math]

which means that in an ensemble of many such spins with slightly different chemical shifts, there is a dephasing of the magnetisation in the [math]\displaystyle{ x }[/math]-[math]\displaystyle{ y }[/math] plane. Consider the pulse sequence

[math]\displaystyle{ \left(\frac{\pi}{2}\right)_x }[/math] — [math]\displaystyle{ \tau }[/math] — [math]\displaystyle{ (\pi)_x }[/math] — [math]\displaystyle{ \tau, }[/math]

where [math]\displaystyle{ \tau }[/math] is a time interval. Starting in an equilibrium state with all the polarisation along the [math]\displaystyle{ z }[/math]-axis, the evolution of an individual spin in the ensemble is

[math]\displaystyle{ \begin{align} L_z \xrightarrow{\left(\frac{\pi}{2}\right)_x} -L_y \xrightarrow{\omega L_z t} -L_y\cos\omega t + L_x\sin\omega t \xrightarrow{(\pi)_x} L_y\cos\omega t + L_x\sin\omega t \xrightarrow{\omega L_z t} &(L_y\cos\omega t - L_x\sin\omega t)\cos\omega t + (L_x \cos\omega t + L_y \sin\omega t)\sin\omega t\\ &= L_y(\cos^2\omega t + \sin^2\omega t) + L_x (-\sin\omega t \cos\omega t + \cos\omega t \sin\omega t)\\ &= L_y. \end{align} }[/math]

Hence this sequence refocuses the transverse magnetisation produced by the first pulse, independent of the value of the chemical shift.

As an indication of the utility of the formalism, suppose instead that we tried to reach the same result using states only and therefore the Schrödinger time evolution operators. This amounts to trying to simplify the unitary propagator [math]\displaystyle{ U }[/math] taking the initial state [math]\displaystyle{ |\psi_0\rangle }[/math]to the final state [math]\displaystyle{ |\psi\rangle }[/math] as [math]\displaystyle{ |\psi\rangle = U|\psi_0\rangle }[/math], where explicitly

[math]\displaystyle{ U = \exp(-\mathrm{i}\omega L_z t)\exp(-\mathrm{i}\pi L_x)\exp(-\mathrm{i}\omega L_z t). }[/math]

Essentially we want to find the propagator in the form [math]\displaystyle{ U = \exp C }[/math], that is as a single exponential of a combination of operators, because that gives the effective Hamiltonian acting during the sequence. Since the arguments of the exponentials in the original form of the propagator do not commute, this amounts to solving a specific example of the Baker–Campbell–Hausdorff (BCH) problem. In this relatively simple case we can solve the BCH problem using the fact that [math]\displaystyle{ U f(A) U^\dagger = f(U A U^\dagger) }[/math] for unitary operator [math]\displaystyle{ U }[/math], operator [math]\displaystyle{ A }[/math] and function [math]\displaystyle{ f }[/math], as well as the mathematical similarity of the spin operators with the physical rotation generators, which allow us to write

[math]\displaystyle{ \exp(\mathrm{i}\pi L_x)\exp(-\mathrm{i}\omega L_z t)\exp(-\mathrm{i}\pi L_x) = \exp\left[-\mathrm{i}\omega t\exp(\mathrm{i}\pi L_x)L_z\exp(-\mathrm{i}\pi L_x)\right] = \exp(\mathrm{i}\omega L_z t) \implies \exp(-\mathrm{i}\omega L_z t)\exp(-\mathrm{i}\pi L_x) = \exp(-\mathrm{i}\pi L_x)\exp(\mathrm{i}\omega L_z t). }[/math]

Hence [math]\displaystyle{ U = \exp(-\mathrm{i}\pi L_x) }[/math] and only the effect of the 180° pulse remains, which agrees with the product operator treatment. For larger sequences of pulses this state treatment quickly becomes even more unwieldy, unless more advanced methods such as exact effective Hamiltonian theory (which gives closed-form expressions for the entangled propagators via the Cayley-Hamilton theorem and eigendecompositions) are used.

The amplitude of a Hahn echo in an inhomogeneous magnetic field

As an extension of the refocussing pulse treated above, consider a set of two pulses with arbitrary flip angles [math]\displaystyle{ \alpha_1 }[/math] and [math]\displaystyle{ \alpha_2 }[/math], that is sequence

[math]\displaystyle{ \left(\alpha_1\right)_x }[/math] — [math]\displaystyle{ \tau }[/math] — [math]\displaystyle{ \left(\alpha_2\right)_x }[/math] — [math]\displaystyle{ \tau, }[/math]

where again [math]\displaystyle{ \tau }[/math] is a time interval. Liberally dropping irrelevant terms, the evolution for a single spin with offset [math]\displaystyle{ \omega }[/math] up to just after the second pulse is

[math]\displaystyle{ L_z \xrightarrow{\left(\alpha_1\right)_x} - L_y \sin\alpha_1 + \cdots \xrightarrow{\omega L_z t} - L_y \sin\alpha_1 \cos\omega t + L_x \sin\alpha_1 \sin\omega t + \cdots \xrightarrow{\left(\alpha_2\right)_x} L_x \sin\alpha_1 \sin\omega t - L_y \sin\alpha_1 \cos\alpha_2 \cos\omega t + \cdots. }[/math]

Now consider an ensemble of spins in a magnetic field that is sufficiently inhomogeneous to completely dephase the spins in the interval between the pulses. After the second pulse, we can decompose the remaining terms into a sum of two spin populations differing only in the sign of the [math]\displaystyle{ L_y }[/math] term, in the sense that for an individual spin we have

[math]\displaystyle{ L_x \sin\omega t - \cos\alpha_2\, L_y \cos\omega t = \cos^2\frac{\alpha_2}{2}\,(L_x\sin\omega t - L_y\cos\omega t) + \sin^2\frac{\alpha_2}{2}\, (L_x\sin\omega t + L_y\cos\omega t), }[/math]

where we used the identities [math]\displaystyle{ \cos^2\theta + \sin^2\theta = 1 }[/math] and [math]\displaystyle{ \cos^2\theta - \sin^2\theta = \cos2\theta }[/math].

It is the spins in the new population that has been generated by the second pulse, namely the one with [math]\displaystyle{ +L_y }[/math], that will lead to the formation of an echo after evolution for the next [math]\displaystyle{ \tau }[/math] interval. Therefore, remembering to include the [math]\displaystyle{ \sin\alpha_1 }[/math] introduced by the first pulse, the amplitude of the resulting Hahn echo relative to that produced by an ideal 90°—180° refocussing pulse sequence is roughly

[math]\displaystyle{ \sin\alpha_1\sin^2\frac{\alpha_2}{2}. }[/math]

Note that this is not an exact result, because it considers only the refocussing of polarisation that was transverse immediately before the second pulse. In reality there will be further transverse components originating from the tipping of the longitudinal magnetisation that remained after the first pulse. However, for many tip angles, this is a good rule of thumb.

To instead arrive at this result using the state formalism, we would have had to non-trivially evaluate the rotation propagator as

[math]\displaystyle{ U(\alpha) = \exp(-\mathrm{i}\alpha L_x) = \cos\frac{\alpha}{2}\, \mathbf{1} - 2\mathrm{i}\sin\frac{\alpha}{2}\, L_x, }[/math]

and then evaluate a transition probability by considering the result of applying this to a state representing polarisation in the transverse plane.

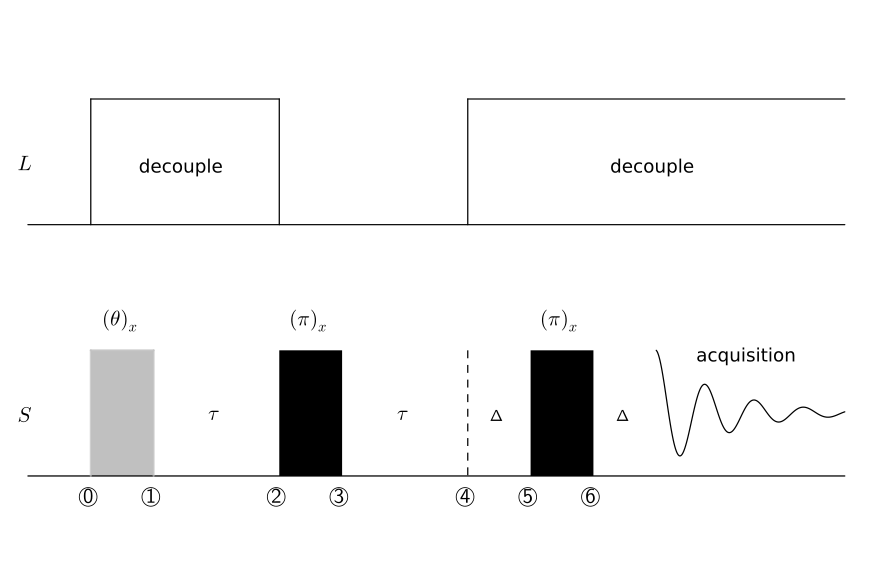
DEPT (Distortionless Enhancement by Polarisation Transfer)

DEPT (Distortionless Enhancement by Polarisation Transfer) is a pulse sequence used to distinguish between the multiplicity of hydrogen bonded to carbon, that is it can separate C, CH, CH₂ and CH₃ groups. It does this by exploiting the heteronuclear carbon-hydrogen [math]\displaystyle{ J }[/math]-coupling and varying the tip angle of the final pulse in the sequence. The basic pulse sequence is shown below.

Under the weak coupling assumption, the chemical shift terms commute with the [math]\displaystyle{ J }[/math]-coupling term in the Hamiltonian. Hence we can ignore the refocussed chemical shift (see § The 180°-refocussing pulse) in the two intervals containing [math]\displaystyle{ \pi }[/math]-pulses, namely [math]\displaystyle{ (1)\to(4) }[/math] and [math]\displaystyle{ (3)\to(6) }[/math], and additionally refrain from evaluating the chemical shift evolution in the last [math]\displaystyle{ \frac{\tau}{2} }[/math] period [math]\displaystyle{ (5)\to(6) }[/math]. The pulse separation time [math]\displaystyle{ \frac{\tau}{2} }[/math] is adjusted to the coupling strength [math]\displaystyle{ J }[/math] (with associated Hamiltonian coefficient [math]\displaystyle{ \alpha = \pi J }[/math]) such that it satisfies

[math]\displaystyle{ \frac{\tau}{2}\cdot\pi J = \frac{\pi}{2} \implies \tau = \frac{1}{J} }[/math],

because then the first term in the evolved density operator in Equation 2 vanishes under the pure coupling evolution between the pulses.

CH

Label the hydrogen spin as [math]\displaystyle{ L }[/math], and the carbon spin by [math]\displaystyle{ S }[/math]. For illustrative purposes, we assume that the equilibrium state only has polarisation on the [math]\displaystyle{ L }[/math]-spin (in reality, there will also be polarisation on the [math]\displaystyle{ S }[/math] spin, with the relative populations determined by the thermal Boltzmann factors). The [math]\displaystyle{ J }[/math]-coupling Hamiltonian is

[math]\displaystyle{ H = \pi J\, 2 L_z S_z }[/math]

which gives the following evolution

[math]\displaystyle{ \begin{align} (0)&:\ L_z\\ (0)\to(1)&:\ L_z \xrightarrow{\left(\frac{\pi}{2}\right)_{xL}} -L_y\\ (1)\to(2)&:\ {-L_y} \xrightarrow{J-\text{coup.}} 2 L_x S_z\\ (2)\to(3)&:\ 2 L_x S_z \xrightarrow{\left(\frac{\pi}{2}\right)_{xS}} -2 L_x S_y \xrightarrow{\left(\pi\right)_{xL}} -2 L_x S_y\\ (3)\to(4)&:\ {-2 L_x S_y} \xrightarrow{J-\text{coup.}} {-2 L_x S_y}\\ (4)\to(5)&:\ {-2 L_x S_y} \xrightarrow{\left(\pi\right)_{xS}} 2 L_x S_y \xrightarrow{(\theta)_{yL}} 2 L_x S_y \cos\theta - 2 L_z S_y \sin\theta\\ (5)\to(6)&:\ {2 L_x S_y \cos\theta - 2 L_z S_y \sin\theta} \xrightarrow{J-\text{coup.}} 2 L_x S_y \cos\theta + S_x\sin\theta \end{align} }[/math]

The non-trivial commutators used to identify the cyclic subspace for [math]\displaystyle{ (1) \to (2) }[/math] are

[math]\displaystyle{ \begin{align} \left.[L_y, 2 L_z S_z]\right. &= 2(L_y \otimes \mathbf{1}_L)(L_z \otimes S_z) - 2(L_z \otimes S_z)(L_y \otimes \mathbf{1}_L)\\ &= 2L_y L_z \otimes S_z - 2L_z L_y \otimes S_z\\ &= 2[L_y, L_z] \otimes S_z\\ &= \mathrm{i} 2 L_x S_z, \end{align} }[/math]

and consequently the next cyclic rotation

[math]\displaystyle{ \begin{align} \left.[2 L_z S_z, 2 L_x S_z]\right. &= 4[L_z, L_x]\otimes S_z^2\\ &= 4\mathrm{i}\, L_y \otimes \frac{1}{4}\mathbf{1}_S\\ &= \mathrm{i}L_y, \end{align} }[/math]

where we used the 'mixed-product identity' [math]\displaystyle{ (A \otimes B)(C \otimes D) = AC \otimes BD }[/math], which relates the matrix and Kronecker products for compatible dimensions of [math]\displaystyle{ A,B,C,D }[/math], and also the fact that since the two eigenvalues of any of the spin-1/2 operators [math]\displaystyle{ S_x, S_y, S_z }[/math] are [math]\displaystyle{ s = \pm \frac{1}{2} }[/math], any of their squares are given by [math]\displaystyle{ s^2 \mathbf{1}_S }[/math] by the Cayley–Hamilton theorem.

Note also that the [math]\displaystyle{ 2L_x L_y }[/math] term is invariant under the [math]\displaystyle{ J }[/math]-coupling evolution. That is that the term commutes with the Hamiltonian, and in this case, that can be manually confirmed by evaluating the commutator [math]\displaystyle{ [2 L_x L_y, 2 L_z S_z] = 0 }[/math] using the matrix representations of the spin operators.

CH₂

Now label the two hydrogen spins as [math]\displaystyle{ L, L' }[/math] and the carbon spin by [math]\displaystyle{ S }[/math]. The [math]\displaystyle{ J }[/math]-coupling Hamiltonian is now

[math]\displaystyle{ H = \pi J (2 L_z S_z + 2 L_z' S_z) }[/math]

which gives the following evolution

[math]\displaystyle{ \begin{align} (0)&:\ L_z + L_z'\\ (0)\to(1)&:\ L_z + L_z' \xrightarrow{\left(\frac{\pi}{2}\right)_{xL}} -L_y + L_z' \xrightarrow{\left(\frac{\pi}{2}\right)_{xL'}} -L_y - L_y'\\ (1)\to(2)&:\ {-L_y - L_y'} \xrightarrow{J-\text{coup.}} 2 L_x S_z + 2 L_x' S_z\\ (2)\to(3)&:\ 2 L_x S_z + 2 L_x' S_z\xrightarrow{\left(\frac{\pi}{2}\right)_{xS}} -2 L_x S_y - 2 L_x' S_y \xrightarrow{\left(\pi\right)_{xL}} -2 L_x S_y - 2 L_x' S_y \xrightarrow{\left(\pi\right)_{xL'}} -2 L_x S_y - 2 L_x' S_y\\ (3)\to(4)&:\ -2 L_x S_y - 2 L_x' S_y \xrightarrow{J-\text{coup.}} 4 L_x L_z' S_x + 4 L_z L_x' S_x\\ (4)\to(5)&:\ 4 L_x L_z' S_x + 4 L_z L_x' S_x \xrightarrow{\left(\pi\right)_{xS}} 4 L_x L_z' S_x + 4 L_z L_x' S_x \xrightarrow{(\theta)_{yL}} 4 L_z L_x' S_x \cos\theta - 4 L_z L_z' S_x \sin\theta + \text{others} \xrightarrow{(\theta)_{yL'}} -8 L_zL_z' S_x \cos\theta\sin\theta + \text{others}\\ (5)\to(6)&:\ -8 L_zL_z' S_x \cos\theta\sin\theta + \text{others} \xrightarrow{J_{LS}-\text{coup.}} -4 L_z' S_y \cos\theta\sin\theta + \text{others} \xrightarrow{J_{L'S}-\text{coup.}} 2 S_x \cos\theta\sin\theta + \text{others} \end{align} }[/math]

where 'others' denotes various terms that can safely be ignored because they will not evolve into observable transverse polarisation on the target spin [math]\displaystyle{ S }[/math]. The required cyclic commutators for dealing with the [math]\displaystyle{ J }[/math]-coupling evolution are the following three sets (and their [math]\displaystyle{ L \leftrightarrow L' }[/math] versions if needed)

[math]\displaystyle{ \begin{align} \left.[L_x S_y, 2L_z' S_z]\right. &= 2L_x \otimes L_z' \otimes [S_y, S_z]\\ &= \mathrm{i}\, 2 L_x L_z' S_x \end{align} }[/math]

[math]\displaystyle{ \begin{align} \left.[2 L_z' S_z, 2 L_x L_z' S_x]\right. &= 4 L_x \otimes {L_z'}^2 \otimes [S_z, S_x]\\ &= 4 L_x \otimes \frac{1}{4}\mathbf{1}_{L'} \otimes \mathrm{i} S_y\\ &= \mathrm{i} L_x S_y, \end{align} }[/math]

[math]\displaystyle{ \begin{align} \left.[2 L_z L_z' S_x, 2 L_z S_z]\right. &= 4L_z^2 \otimes L_z' \otimes [S_x, S_z]\\ &= 4\cdot\frac{1}{4}\mathbf{1}_L \otimes L_z' \otimes -\mathrm{i} S_y\\ &= \mathrm{i} \cdot -L_z' S_y \end{align} }[/math]

[math]\displaystyle{ \begin{align} \left.[2 L_z L_z, -L_z' S_y]\right. &= -L_z \otimes L_z' \otimes [S_z, S_y]\\ &= \mathrm{i}\, 2L_z L_z' S_x, \end{align} }[/math]

[math]\displaystyle{ \begin{align} \left.[2 L_z' S_y, 2 L_z' S_z]\right. &= 4\mathbf{1}_L \otimes L_z'^2 \otimes [S_y, S_z]\\ &= 4\mathbf{1}_L \otimes \frac{1}{4}\mathbf{1}_{L'} \otimes \mathrm{i} S_x\\ &= \mathrm{i} S_x \end{align} }[/math]

[math]\displaystyle{ \begin{align} \left.[2 L_z' S_z, S_x]\right. &= 2\mathbf{1}_L \otimes L_z' \otimes [S_z, S_x]\\ &= \mathrm{i}\, 2 L_z' \otimes S_y. \end{align} }[/math]

CH₃

A similar (but more lengthy) treatment gives the final observable term as [math]\displaystyle{ 3 S_x \cos^2\theta\sin\theta }[/math].

APT (Attached Proton Test)

Refer to § DEPT (Distortionless Enhancement by Polarisation Transfer) for the notation used in this example.

APT is similar to DEPT in that it detects carbon multiplicity. However, it has additional degeneracies: it gives identical positive signals for C and CH₂, and identical negative signals for CH and CH₃. One variation on the basic pulse sequence is shown below.

The key observation is that since we can again ignore the refocussed chemical shift, the only relevant dynamics occur in the interval with no hydrogen decoupling, where we can consider solely the [math]\displaystyle{ J }[/math]-coupling. By using an interval twice as long as in the DEPT case, we ensure that a density operator of [math]\displaystyle{ L_y }[/math] at the start of the interval just has its sign inverted following the coupling (since this corresponds to [math]\displaystyle{ \alpha t=\pi }[/math] in the general treatment, and [math]\displaystyle{ \cos\pi = -1,\, \sin\pi = 0 }[/math]). The Hamiltonians for the couplings to each of the [math]\displaystyle{ n }[/math] separate neighbouring hydrogen atoms commute, so the overall effect is to multiply by a factor [math]\displaystyle{ (-1)^n }[/math]. This motivates the alternating sign of the signal mentioned above.

References

• James Keeler. "Understanding NMR Spectroscopy" (reprinted at University of Cambridge). University of California, Irvine. http://www-keeler.ch.cam.ac.uk/lectures/Irvine/. Retrieved 2012-08-05. 
• David Donne; David Gorenstein. "A Pictorial Representation of Product Operator Formalism". University of Texas. http://www.biophysics.org/Portals/1/PDFs/Education/donne.pdf. Retrieved 2012-08-05. 
• Hennig, Jürgen (1991). "Echoes—how to generate, recognize, use or avoid them in MR-imaging sequences. Part I: Fundamental and not so fundamental properties of spin echoes". Concepts in Magnetic Resonance 3 (3): 125–143. doi:10.1002/cmr.1820030302. 
• Mateescu, Gheorghe D; Valeriu, Adrian (1993). "2D NMR Density Matrix and Product Operator Treatment". Journal of Chemical Education 70 (6): A172. doi:10.1021/ed070pA172.3. Bibcode: 1993JChEd..70S.172.. 
• Siminovitch, David; Untidt, Thomas; Nielsen, Niels Chr. (2004). "Exact effective Hamiltonian theory. II. Polynomial expansion of matrix functions and entangled unitary exponential operators". The Journal of Chemical Physics 120 (1): 51–66. doi:10.1063/1.1628216. PMID 15267261. Bibcode: 2004JChPh.120...51S. 
• Zhang, Yuning; Han, Fei; Jerschow, Alexej (2013). "Product Operator Formalism". EMag Res. doi:10.1002/9780470034590.emrstm1310. ISBN 978-0470034590.