Physics:Planck constant

From HandWiki
Short description: Physical constant in quantum mechanics
Planck constant
Common symbols
[math]\displaystyle{ h }[/math]
SI unitjoule per hertz (joule seconds)
Other units
electronvolt per hertz (electronvolt seconds)
Dimension[math]\displaystyle{ \mathsf{M} \mathsf{L}^{2} \mathsf{T}^{-1} }[/math]
Reduced Planck constant
Common symbols
[math]\displaystyle{ \hbar }[/math]
SI unitjoule-seconds
Other units
electronvolt-seconds
Derivations from
other quantities
  • [math]\displaystyle{ \hbar {{=}} h/(2 \pi) }[/math]
Dimension[math]\displaystyle{ \mathsf{M} \mathsf{L}^{2} \mathsf{T}^{-1} }[/math]

The Planck constant, or Planck's constant, denoted by [math]\displaystyle{ h }[/math],[1] is a fundamental physical constant[1] of foundational importance in quantum mechanics: a photon's energy is equal to its frequency multiplied by the Planck constant, and the wavelength of a matter wave equals the Planck constant divided by the associated particle momentum.

The constant was postulated by Max Planck in 1900 as a proportionality constant needed to explain experimental black-body radiation.[2] Planck later referred to the constant as the "quantum of action".[3] In 1905, Albert Einstein associated the "quantum" or minimal element of the energy to the electromagnetic wave itself. Max Planck received the 1918 Nobel Prize in Physics "in recognition of the services he rendered to the advancement of Physics by his discovery of energy quanta".

In metrology, the Planck constant is used, together with other constants, to define the kilogram, the SI unit of mass.[4] The SI units are defined in such a way that, when the Planck constant is expressed in SI units, it has the exact value [math]\displaystyle{ h }[/math] = 6.62607015×10−34 J⋅s.[5][6] It is often used with units of electronvolt (eV), which corresponds to the SI unit per elementary charge.

History

Origin of the constant

Main page: Physics:Planck's law
Plaque at the Humboldt University of Berlin: "Max Planck, who discovered the elementary quantum of action h, taught here from 1889 to 1928."
Intensity of light emitted from a black body. Each curve represents behavior at different body temperatures. The Planck constant h is used to explain the shape of these curves.

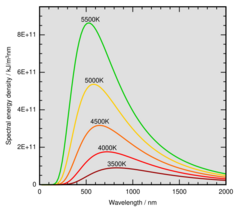
Planck's constant was formulated as part of Max Planck's successful effort to produce a mathematical expression that accurately predicted the observed spectral distribution of thermal radiation from a closed furnace (black-body radiation).[7] This mathematical expression is now known as Planck's law.

In the last years of the 19th century, Max Planck was investigating the problem of black-body radiation first posed by Kirchhoff some 40 years earlier. Every physical body spontaneously and continuously emits electromagnetic radiation. There was no expression or explanation for the overall shape of the observed emission spectrum. At the time, Wien's law fit the data for short wavelengths and high temperatures, but failed for long wavelengths.[7]:141 Also around this time, but unknown to Planck, Lord Rayleigh had derived theoretically a formula, now known as the Rayleigh–Jeans law, that could reasonably predict long wavelengths but failed dramatically at short wavelengths.

Approaching this problem, Planck hypothesized that the equations of motion for light describe a set of harmonic oscillators, one for each possible frequency. He examined how the entropy of the oscillators varied with the temperature of the body, trying to match Wien's law, and was able to derive an approximate mathematical function for the black-body spectrum,[2] which gave a simple empirical formula for long wavelengths.

Planck tried to find a mathematical expression that could reproduce Wien's law (for short wavelengths) and the empirical formula (for long wavelengths). This expression included a constant, [math]\displaystyle{ h }[/math], which is thought to be for Hilfsgrösse (auxiliary variable),[8] and subsequently became known as the Planck constant. The expression formulated by Planck showed that the spectral radiance of a body for frequency ν at absolute temperature T is given by

[math]\displaystyle{ B_\nu(\nu, T) = \frac{ 2 h \nu^3}{c^2} \frac{1}{e^\frac{h\nu}{k_\mathrm B T} - 1} }[/math],

where [math]\displaystyle{ k_\text{B} }[/math] is the Boltzmann constant, [math]\displaystyle{ h }[/math] is the Planck constant, and [math]\displaystyle{ c }[/math] is the speed of light in the medium, whether material or vacuum.[9][10][11]

The spectral radiance of a body, [math]\displaystyle{ B_{\nu} }[/math], describes the amount of energy it emits at different radiation frequencies. It is the power emitted per unit area of the body, per unit solid angle of emission, per unit frequency. The spectral radiance can also be expressed per unit wavelength [math]\displaystyle{ \lambda }[/math] instead of per unit frequency. In this case, it is given by

[math]\displaystyle{ B_\lambda(\lambda, T) =\frac{2hc^2}{\lambda^5}\frac{1}{ e^{\frac{hc}{\lambda k_\mathrm B T}} - 1} }[/math],

showing how radiated energy emitted at shorter wavelengths increases more rapidly with temperature than energy emitted at longer wavelengths.[12]

Planck's law may also be expressed in other terms, such as the number of photons emitted at a certain wavelength, or the energy density in a volume of radiation. The SI units of [math]\displaystyle{ B_{\nu} }[/math] are W·sr−1·m−2·Hz−1, while those of [math]\displaystyle{ B_{\lambda} }[/math] are W·sr−1·m−3.

Planck soon realized that his solution was not unique. There were several different solutions, each of which gave a different value for the entropy of the oscillators.[2] To save his theory, Planck resorted to using the then-controversial theory of statistical mechanics,[2] which he described as "an act of desperation".[13] One of his new boundary conditions was

to interpret UN [the vibrational energy of N oscillators] not as a continuous, infinitely divisible quantity, but as a discrete quantity composed of an integral number of finite equal parts. Let us call each such part the energy element ε;
—Planck, On the Law of Distribution of Energy in the Normal Spectrum[2]

With this new condition, Planck had imposed the quantization of the energy of the oscillators, "a purely formal assumption ... actually I did not think much about it ..." in his own words,[14] but one that would revolutionize physics. Applying this new approach to Wien's displacement law showed that the "energy element" must be proportional to the frequency of the oscillator, the first version of what is now sometimes termed the "Planck–Einstein relation":

[math]\displaystyle{ E = hf. }[/math]

Planck was able to calculate the value of [math]\displaystyle{ h }[/math] from experimental data on black-body radiation: his result, 6.55×10−34 J⋅s, is within 1.2% of the currently defined value.[2] He also made the first determination of the Boltzmann constant [math]\displaystyle{ k_\text{B} }[/math] from the same data and theory.[15]

The observed Planck curves at different temperatures, and the divergence of the theoretical Rayleigh–Jeans (black) curve from the observed Planck curve at 5000K.

Development and application

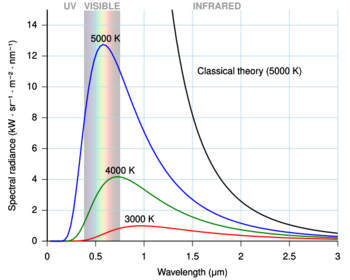
The black-body problem was revisited in 1905, when Lord Rayleigh and James Jeans (on the one hand) and Albert Einstein (on the other hand) independently proved that classical electromagnetism could never account for the observed spectrum. These proofs are commonly known as the "ultraviolet catastrophe", a name coined by Paul Ehrenfest in 1911. They contributed greatly (along with Einstein's work on the photoelectric effect) in convincing physicists that Planck's postulate of quantized energy levels was more than a mere mathematical formalism. The first Solvay Conference in 1911 was devoted to "the theory of radiation and quanta".[16]

Photoelectric effect

Main page: Physics:Photoelectric effect

The photoelectric effect is the emission of electrons (called "photoelectrons") from a surface when light is shone on it. It was first observed by Alexandre Edmond Becquerel in 1839, although credit is usually reserved for Heinrich Hertz,[17] who published the first thorough investigation in 1887. Another particularly thorough investigation was published by Philipp Lenard (Lénárd Fülöp) in 1902.[18] Einstein's 1905 paper[19] discussing the effect in terms of light quanta would earn him the Nobel Prize in 1921,[17] after his predictions had been confirmed by the experimental work of Robert Andrews Millikan.[20] The Nobel committee awarded the prize for his work on the photo-electric effect, rather than relativity, both because of a bias against purely theoretical physics not grounded in discovery or experiment, and dissent amongst its members as to the actual proof that relativity was real.[21][22]

Before Einstein's paper, electromagnetic radiation such as visible light was considered to behave as a wave: hence the use of the terms "frequency" and "wavelength" to characterize different types of radiation. The energy transferred by a wave in a given time is called its intensity. The light from a theatre spotlight is more intense than the light from a domestic lightbulb; that is to say that the spotlight gives out more energy per unit time and per unit space (and hence consumes more electricity) than the ordinary bulb, even though the color of the light might be very similar. Other waves, such as sound or the waves crashing against a seafront, also have their intensity. However, the energy account of the photoelectric effect did not seem to agree with the wave description of light.

The "photoelectrons" emitted as a result of the photoelectric effect have a certain kinetic energy, which can be measured. This kinetic energy (for each photoelectron) is independent of the intensity of the light,[18] but depends linearly on the frequency;[20] and if the frequency is too low (corresponding to a photon energy that is less than the work function of the material), no photoelectrons are emitted at all, unless a plurality of photons, whose energetic sum is greater than the energy of the photoelectrons, acts virtually simultaneously (multiphoton effect).[23] Assuming the frequency is high enough to cause the photoelectric effect, a rise in intensity of the light source causes more photoelectrons to be emitted with the same kinetic energy, rather than the same number of photoelectrons to be emitted with higher kinetic energy.[18]

Einstein's explanation for these observations was that light itself is quantized; that the energy of light is not transferred continuously as in a classical wave, but only in small "packets" or quanta. The size of these "packets" of energy, which would later be named photons, was to be the same as Planck's "energy element", giving the modern version of the Planck–Einstein relation:

[math]\displaystyle{ E = hf . }[/math]

Einstein's postulate was later proven experimentally: the constant of proportionality between the frequency of incident light [math]\displaystyle{ f }[/math] and the kinetic energy of photoelectrons [math]\displaystyle{ E }[/math] was shown to be equal to the Planck constant [math]\displaystyle{ h }[/math].[20]

Atomic structure

Main page: Physics:Bohr model
A schematization of the Bohr model of the hydrogen atom. The transition shown from the n = 3 level to the n = 2 level gives rise to visible light of wavelength 656 nm (red), as the model predicts.

It was John William Nicholson in 1912 who introduced h-bar into the theory of the atom which was the first quantum and nuclear atom and the first to quantize angular momentum as h/2π.[24][25][26][27][28] Niels Bohr quoted him in his 1913 paper of the Bohr model of the atom.[29] The influence of the work of Nicholson's nuclear quantum atomic model on Bohr's model has been written about by many historians.[30][31][28]

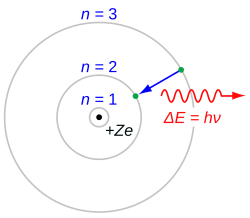
Niels Bohr introduced the third quantized model of the atom in 1913, in an attempt to overcome a major shortcoming of Rutherford's classical model. The first quantized model of the atom was introduced in 1910 by Arthur Erich Haas and was discussed at the 1911 Solvay conference.[24][29] In classical electrodynamics, a charge moving in a circle should radiate electromagnetic radiation. If that charge were to be an electron orbiting a nucleus, the radiation would cause it to lose energy and spiral down into the nucleus. Bohr solved this paradox with explicit reference to Planck's work: an electron in a Bohr atom could only have certain defined energies [math]\displaystyle{ E_n }[/math]

[math]\displaystyle{ E_n = -\frac{h c R_{\infty}}{n^2} , }[/math]

where [math]\displaystyle{ c }[/math] is the speed of light in vacuum, [math]\displaystyle{ R_{\infty} }[/math] is an experimentally determined constant (the Rydberg constant) and [math]\displaystyle{ n \in \{1, 2, 3, ... \} }[/math]. Once the electron reached the lowest energy level ([math]\displaystyle{ n = 1 }[/math]), it could not get any closer to the nucleus (lower energy). This approach also allowed Bohr to account for the Rydberg formula, an empirical description of the atomic spectrum of hydrogen, and to account for the value of the Rydberg constant [math]\displaystyle{ R_{\infty} }[/math] in terms of other fundamental constants.

Bohr also introduced the quantity [math]\displaystyle{ \hbar=\frac{h}{2\pi} }[/math], now known as the reduced Planck constant or Dirac constant, as the quantum of angular momentum. At first, Bohr thought that this was the angular momentum of each electron in an atom: this proved incorrect and, despite developments by Sommerfeld and others, an accurate description of the electron angular momentum proved beyond the Bohr model. The correct quantization rules for electrons – in which the energy reduces to the Bohr model equation in the case of the hydrogen atom – were given by Heisenberg's matrix mechanics in 1925 and the Schrödinger wave equation in 1926: the reduced Planck constant remains the fundamental quantum of angular momentum. In modern terms, if [math]\displaystyle{ J }[/math] is the total angular momentum of a system with rotational invariance, and [math]\displaystyle{ J_z }[/math] the angular momentum measured along any given direction, these quantities can only take on the values

[math]\displaystyle{ \begin{align} J^2 = j(j+1) \hbar^2,\qquad & j = 0, \tfrac{1}{2}, 1, \tfrac{3}{2}, \ldots, \\ J_z = m \hbar, \qquad\qquad\quad & m = -j, -j+1, \ldots, j. \end{align} }[/math]

Uncertainty principle

Main page: Physics:Uncertainty principle

The Planck constant also occurs in statements of Werner Heisenberg's uncertainty principle. Given numerous particles prepared in the same state, the uncertainty in their position, [math]\displaystyle{ \Delta x }[/math], and the uncertainty in their momentum, [math]\displaystyle{ \Delta p_{x} }[/math], obey

[math]\displaystyle{ \Delta x\, \Delta p_{x} \ge \frac{\hbar}{2} , }[/math]

where the uncertainty is given as the standard deviation of the measured value from its expected value. There are several other such pairs of physically measurable conjugate variables which obey a similar rule. One example is time vs. energy. The inverse relationship between the uncertainty of the two conjugate variables forces a tradeoff in quantum experiments, as measuring one quantity more precisely results in the other quantity becoming imprecise.

In addition to some assumptions underlying the interpretation of certain values in the quantum mechanical formulation, one of the fundamental cornerstones to the entire theory lies in the commutator relationship between the position operator [math]\displaystyle{ \hat{x} }[/math] and the momentum operator [math]\displaystyle{ \hat{p} }[/math]:

[math]\displaystyle{ [\hat{p}_i, \hat{x}_j] = -i \hbar \delta_{ij} , }[/math]

where [math]\displaystyle{ \delta_{ij} }[/math] is the Kronecker delta.

Photon energy

The Planck relation connects the particular photon energy E with its associated wave frequency f:

[math]\displaystyle{ E = hf. }[/math]

This energy is extremely small in terms of ordinarily perceived everyday objects.

Since the frequency f, wavelength λ, and speed of light c are related by [math]\displaystyle{ f= \frac{c}{\lambda} }[/math], the relation can also be expressed as

[math]\displaystyle{ E = \frac{hc}{\lambda} . }[/math]

de Broglie wavelength

In 1923, Louis de Broglie generalized the Planck–Einstein relation by postulating that the Planck constant represents the proportionality between the momentum and the quantum wavelength of not just the photon, but the quantum wavelength of any particle. This was confirmed by experiments soon afterward. This holds throughout the quantum theory, including electrodynamics. The de Broglie wavelength λ of the particle is given by

[math]\displaystyle{ \lambda = \frac{h}{p}, }[/math]

where p denotes the linear momentum of a particle, such as a photon, or any other elementary particle.

The energy of a photon with angular frequency ω = 2πf is given by

[math]\displaystyle{ E = \hbar \omega , }[/math]

while its linear momentum relates to

[math]\displaystyle{ p = \hbar k , }[/math]

where k is an angular wavenumber.

These two relations are the temporal and spatial parts of the special relativistic expression using 4-vectors.

[math]\displaystyle{ P^\mu = \left(\frac{E}{c}, \vec{p}\right) = \hbar K^\mu = \hbar\left(\frac{\omega}{c}, \vec{k}\right). }[/math]

Statistical mechanics

Classical statistical mechanics requires the existence of h (but does not define its value).[32] Eventually, following upon Planck's discovery, it was speculated that physical action could not take on an arbitrary value, but instead was restricted to integer multiples of a very small quantity, the "[elementary] quantum of action", now called the Planck constant.[33] This was a significant conceptual part of the so-called "old quantum theory" developed by physicists including Bohr, Sommerfeld, and Ishiwara, in which particle trajectories exist but are hidden, but quantum laws constrain them based on their action. This view has been replaced by fully modern quantum theory, in which definite trajectories of motion do not even exist; rather, the particle is represented by a wavefunction spread out in space and in time. Related to this is the concept of energy quantization which existed in old quantum theory and also exists in altered form in modern quantum physics. Classical physics cannot explain either quantization of energy or the lack of classical particle motion.

In many cases, such as for monochromatic light or for atoms, quantization of energy also implies that only certain energy levels are allowed, and values in between are forbidden.[34]

Dimension and value

The Planck constant has the same dimensions as action and as angular momentum. In SI units, the Planck constant is expressed with the unit joule per hertz (J⋅Hz−1) or joule-second (J⋅s).

[math]\displaystyle{ h = \mathrm{6.626\ 070\ 15\times 10^{-34} {J \cdot s}} }[/math] [math]\displaystyle{ \hbar = {h \over 2\pi} = \mathrm{1.054\ 571\ 817...\times 10^{-34} \ {J \cdot s}} = \mathrm{ 6.582\ 119\ 569... \times 10^{-16}\ {eV \cdot s}}. }[/math]

The above values have been adopted as fixed in the 2019 redefinition of the SI base units.

Since 2019, the numerical value of the Planck constant has been fixed, with a finite decimal representation. This fixed value is used to define the Si unit of mass, the kilogram: "the kilogram [...] is defined by taking the fixed numerical value of h to be 6.62607015×10−34 when expressed in the unit J⋅s, which is equal to kg⋅m2⋅s−1, where the metre and the second are defined in terms of speed of light c and duration of hyperfine transition of the ground state of an unperturbed caesium-133 atom ΔνCs."[35] Technologies of mass metrology such as the Kibble balance measure refine the value of kilogram applying fixed value of the Planck constant.

Significance of the value

The Planck constant is one of the smallest constants used in physics. This reflects the fact that on a scale adapted to humans, where energies are typical of the order of kilojoules and times are typical of the order of seconds or minutes, the Planck constant is very small. When the product of energy and time for a physical event approaches the Planck constant, quantum effects dominate.[36]

Equivalently, the order of the Planck constant reflects the fact that everyday objects and systems are made of a large number of microscopic particles. For example, in green light (with a wavelength of 555 nanometres or a frequency of 540 THz) each photon has an energy E = hf = 3.58×10−19 J. That is a very small amount of energy in terms of everyday experience, but everyday experience is not concerned with individual photons any more than with individual atoms or molecules. An amount of light more typical in everyday experience (though much larger than the smallest amount perceivable by the human eye) is the energy of one mole of photons; its energy can be computed by multiplying the photon energy by the Avogadro constant, NA = 6.02214076×1023 mol−1[37], with the result of 216 kJ, about the food energy in three apples.[citation needed]

Reduced Planck constant ℏ

In many applications, the Planck constant [math]\displaystyle{ h }[/math] naturally appears in combination with [math]\displaystyle{ 2\pi }[/math] as [math]\displaystyle{ h/(2\pi) }[/math], which can be traced to the fact that in these applications it is natural to use the angular frequency (in radians per second) rather than plain frequency (in cycles per second or hertz). For this reason, it is often useful to absorb that factor of 2π into the Planck constant by introducing the reduced Planck constant[38][39](p482) (or reduced Planck's constant[40](p5) [41](p788)), equal to the Planck constant divided by [math]\displaystyle{ 2 \pi }[/math][38] and denoted by [math]\displaystyle{ \hbar }[/math] (pronounced h-bar[42](p336)).

Many of the most important equations, relations, definitions, and results of quantum mechanics are customarily written using the reduced Planck constant [math]\displaystyle{ \hbar }[/math] rather than the Planck constant [math]\displaystyle{ h }[/math], including the Schrödinger equation, momentum operator, canonical commutation relation, Heisenberg's uncertainty principle, and Planck units.[43](p104)

Because the fundamental equations look simpler when written using [math]\displaystyle{ \hbar }[/math] as opposed to [math]\displaystyle{ h }[/math], it is usually [math]\displaystyle{ \hbar }[/math] rather than [math]\displaystyle{ h }[/math] that gives the most reliable results when used in order-of-magnitude estimates.[44](pp8–9) [lower-alpha 1]

Names

The reduced Planck constant is known by many other names: the rationalized Planck constant[47](p726) [48](p10) [49](p-) (or rationalized Planck's constant[50](p334) [51](pix) [52](p112) ), the Dirac constant[53](p275) [47](p726) [54](pxv) (or Dirac's constant[55](p148) [56](p604) [57](p313)), the Dirac [math]\displaystyle{ h }[/math][58][59](pxviii) (or Dirac's [math]\displaystyle{ h }[/math][60](p17) ), the Dirac [math]\displaystyle{ \hbar }[/math][61](p187) (or Dirac's [math]\displaystyle{ \hbar }[/math][62](p273) [63](p14) ), and h-bar.[64](p558)[65](p561) It is also common to refer to this [math]\displaystyle{ \hbar }[/math] as “Planck's constant”[66](p55) [lower-alpha 2] while retaining the relationship [math]\displaystyle{ \hbar\, {{=}} h/(2 \pi) }[/math].

Symbols

By far the most common symbol for the reduced Planck constant is [math]\displaystyle{ \hbar }[/math] . However, there are some sources that denote it by [math]\displaystyle{ h }[/math] instead, in which case they usually refer to it as the “Dirac [math]\displaystyle{ h }[/math]”[92](p43) [93](p151) (or “Dirac's [math]\displaystyle{ h }[/math]”[94](p21)).

History

The combination [math]\displaystyle{ h/(2\pi) }[/math] first made its appearance[lower-alpha 3] in Niels Bohr's 1913 paper,[99](p15) where it was denoted by [math]\displaystyle{ M_{0} }[/math].[lower-alpha 4] For the next 15 years, the combination continued to appear in the literature, but normally without a separate symbol.[lower-alpha 5] Then, in 1926, in their seminal papers, Schrödinger and Dirac again introduced special symbols for it: [math]\displaystyle{ K }[/math] in the case of Schrödinger,[112] and [math]\displaystyle{ h }[/math] in the case of Dirac.[113] Dirac continued to use [math]\displaystyle{ h }[/math] in this way until 1930,[114](p291) when he introduced the symbol [math]\displaystyle{ \hbar }[/math] in his book The Principles of Quantum Mechanics.[114](p291) [115]

See also

Notes

  1. ↑ As examples, the preceding reference shows what happens when one uses dimensional analysis to obtain estimates for the ionization energy and the size of a hydrogen atom. If we use the Gaussian units, then the relevant parameters that determine the ionization energy [math]\displaystyle{ E_{\text{i}} }[/math] are the mass of the electron [math]\displaystyle{ m_{\text{e}} }[/math], the electron charge [math]\displaystyle{ e }[/math], and either the Planck constant [math]\displaystyle{ h }[/math] or the reduced Planck constant [math]\displaystyle{ \hbar }[/math] (since [math]\displaystyle{ h }[/math] and [math]\displaystyle{ \hbar }[/math] have the same dimensions, they will enter the dimensional analysis in the same way). One obtains that [math]\displaystyle{ E_{\text{i}} }[/math] must be proportional to [math]\displaystyle{ m_{\text{e}} e^{4}/h^{2} }[/math] if we used [math]\displaystyle{ h }[/math], and to [math]\displaystyle{ m_{\text{e}} e^{4}/\hbar^{2} }[/math] is we used [math]\displaystyle{ \hbar }[/math]. In an order-of-magnitude estimate, we take that the constant of proportionality is 1. Now, the actual correct answer is [math]\displaystyle{ E_{\text{i}}=m_{\text{e}} e^{4}/(2\hbar^{2}) }[/math];[45](p45) therefore, if we choose to use [math]\displaystyle{ \hbar }[/math] as one of our parameters, our estimate will off by a factor of 2, whereas if we choose to use [math]\displaystyle{ h }[/math], it will be off by a factor of [math]\displaystyle{ 4\pi^{2}/2 \approx 20 }[/math]. Similarly for the estimate of the size of a hydrogen atom: depending on whether we use [math]\displaystyle{ h }[/math] or [math]\displaystyle{ \hbar }[/math] as one of the parameters, we get either [math]\displaystyle{ h^{2}/(m_{\text{e}} e^{2}) }[/math] or [math]\displaystyle{ \hbar^{2}/(m_{\text{e}} e^{2}) }[/math]. The latter happens to be exactly correct,[46] whereas the estimate using [math]\displaystyle{ h }[/math] is off by a factor of [math]\displaystyle{ 4\pi^{2} \approx 40 }[/math].
  2. ↑ Notable examples of such usage include Landau and Lifshitz[67](p20) and Giffiths,[68](p3) but there are many others, e.g.[69][70](p449) [71](p284) [72](p3) [73](p365) [74](p14) [75](p18) [76](p4) [77](p138) [78](p251) [79](p1) [80](p622) [81](pxx) [82](p20) [83](p4) [84](p36) [85](p41) [86](p199) [87](p846) [88][89][90](p25) [91](pp653)
  3. ↑ Some sources[95][96]:169 [97](p180) claim that John William Nicholson discovered the quantization of angular momentum in units of [math]\displaystyle{ h/(2\pi) }[/math] in his 1912 paper,[98] so prior to Bohr. True, Bohr does credit Nicholson for emphasizing “the possible importance of the angular momentum in the discussion of atomic systems in relation to Planck's theory.”[99](p15) However, in his paper, Nicholson deals exclusively with the quantization of energy, not angular momentum—with the exception of one paragraph in which he says, if, therefore, the constant [math]\displaystyle{ h }[/math] of Planck has, as Sommerfeld has suggested, an atomic significance, it may mean that the angular momentum of an atom can only rise or fall by discrete amounts when electrons leave or return. It is readily seen that this view presents less difficulty to the mind than the more usual interpretation, which is believed to involve an atomic constitution of energy itself,[98]:679 and with the exception of the following text in the summary: in the present paper, the suggested theory of the coronal spectrum has been put upon a definite basis which is in accord with the recent theories of emission of energy by bodies. It is indicated that the key to the physical side of these theories lies in the fact that an expulsion or retention of an electron by any atom probably involves a discontinuous change in the angular momentum of the atom, which is dependent on the number of electrons already present.[98]:692 The literal combination [math]\displaystyle{ h/(2\pi) }[/math] does not appear in that paper. A biographical memoir of Nicholson[100] states that Nicholson only “later” realized that the discrete changes in angular momentum are integral multiples of [math]\displaystyle{ h/(2\pi) }[/math], but unfortunately the memoir does not say if this realization occurred before or after Bohr published his paper, or whether Nicholson ever published it.
  4. ↑ Bohr denoted by [math]\displaystyle{ M }[/math] the angular momentum of the electron around the nucleus, and wrote the quantization condition as [math]\displaystyle{ M=\tau M_{0} }[/math], where [math]\displaystyle{ \tau }[/math] is a positive integer. (See the Bohr model.)
  5. ↑ Here are some papers that are mentioned in[97] and in which [math]\displaystyle{ h/(2\pi) }[/math] appeared without a separate symbol: [101](p428) [102](p549) [103](p508) [104](p230) [105](p458) [106][107](p276) [108][109][110].[111]

References

Citations

  1. ↑ 1.0 1.1 "Planck constant". NIST. 20 May 2019. https://physics.nist.gov/cgi-bin/cuu/Value?h. 
  2. ↑ 2.0 2.1 2.2 2.3 2.4 2.5 Planck, Max (1901), "Ueber das Gesetz der Energieverteilung im Normalspectrum", Ann. Phys. 309 (3): 553–63, doi:10.1002/andp.19013090310, Bibcode: 1901AnP...309..553P, http://www.physik.uni-augsburg.de/annalen/history/historic-papers/1901_309_553-563.pdf, retrieved 2008-12-15 . English translation: "On the Law of Distribution of Energy in the Normal Spectrum". http://dbhs.wvusd.k12.ca.us/webdocs/Chem-History/Planck-1901/Planck-1901.html. ". "On the Law of Distribution of Energy in the Normal Spectrum". http://theochem.kuchem.kyoto-u.ac.jp/Ando/planck1901.pdf. 
  3. ↑ "Max Planck Nobel Lecture". https://www.nobelprize.org/prizes/physics/1918/planck/lecture/. 
  4. ↑ International Bureau of Weights and Measures (2019-05-20), SI Brochure: The International System of Units (SI) (9th ed.), p. 131, ISBN 978-92-822-2272-0, https://www.bipm.org/utils/common/pdf/si-brochure/SI-Brochure-9.pdf 
  5. ↑ "2018 CODATA Value: Planck constant". The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. http://physics.nist.gov/cgi-bin/cuu/Value?h. Retrieved 2019-05-20. 
  6. ↑ "Resolutions of the 26th CGPM" (in en-GB). 2018-11-16. https://www.bipm.org/utils/common/pdf/CGPM-2018/26th-CGPM-Resolutions.pdf. 
  7. ↑ 7.0 7.1 Bitter, Francis; Medicus, Heinrich A. (1973). Fields and particles. New York: Elsevier. pp. 137–144. 
  8. ↑ Boya, Luis J. (2004). "The Thermal Radiation Formula of Planck (1900)". arXiv:physics/0402064v1.
  9. ↑ Planck, M. (1914). The Theory of Heat Radiation. Masius, M. (transl.) (2nd ed.). P. Blakiston's Son. pp. 6, 168. https://archive.org/details/theoryofheatradi00planrich. 
  10. ↑ Chandrasekhar, S. (1960). Radiative Transfer (Revised reprint ed.). Dover. p. 8. ISBN 978-0-486-60590-6. https://archive.org/details/radiativetransfe0000chan. 
  11. ↑ Rybicki, G. B.; Lightman, A. P. (1979). Radiative Processes in Astrophysics. John Wiley & Sons. p. 22. ISBN 978-0-471-82759-7. https://books.google.com/books?id=LtdEjNABMlsC. Retrieved 2020-05-20. 
  12. ↑ Shao, Gaofeng (2019). "Improved oxidation resistance of high emissivity coatings on fibrous ceramic for reusable space systems". Corrosion Science 146: 233–246. doi:10.1016/j.corsci.2018.11.006. 
  13. ↑ Kragh, Helge (1 December 2000), Max Planck: the reluctant revolutionary, PhysicsWorld.com, https://physicsworld.com/a/max-planck-the-reluctant-revolutionary/ 
  14. ↑ Kragh, Helge (1999), Quantum Generations: A History of Physics in the Twentieth Century, Princeton University Press, p. 62, ISBN 978-0-691-09552-3, https://books.google.com/books?id=ELrFDIldlawC, retrieved 2021-10-31 
  15. ↑ Planck, Max (2 June 1920), The Genesis and Present State of Development of the Quantum Theory (Nobel Lecture), http://nobelprize.org/nobel_prizes/physics/laureates/1918/planck-lecture.html, retrieved 13 December 2008 
  16. ↑ Previous Solvay Conferences on Physics, International Solvay Institutes, http://www.solvayinstitutes.be/Conseils%20Solvay/PreviousPhysics.html, retrieved 12 December 2008 
  17. ↑ 17.0 17.1 See, e.g., Arrhenius, Svante (10 December 1922), Presentation speech of the 1921 Nobel Prize for Physics, http://nobelprize.org/nobel_prizes/physics/laureates/1921/press.html, retrieved 13 December 2008 
  18. ↑ 18.0 18.1 18.2 Lenard, P. (1902), "Ueber die lichtelektrische Wirkung", Annalen der Physik 313 (5): 149–98, doi:10.1002/andp.19023130510, Bibcode: 1902AnP...313..149L, https://zenodo.org/record/1424009, retrieved 2019-07-03 
  19. ↑ Einstein, Albert (1905), "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt", Annalen der Physik 17 (6): 132–48, doi:10.1002/andp.19053220607, Bibcode: 1905AnP...322..132E, http://www.physik.uni-augsburg.de/annalen/history/einstein-papers/1905_17_132-148.pdf, retrieved 2009-12-03 
  20. ↑ 20.0 20.1 20.2 Millikan, R. A. (1916), "A Direct Photoelectric Determination of Planck's h", Physical Review 7 (3): 355–88, doi:10.1103/PhysRev.7.355, Bibcode: 1916PhRv....7..355M 
  21. ↑ Isaacson, Walter (2007-04-10), Einstein: His Life and Universe, Simon and Schuster, ISBN 978-1-4165-3932-2, https://books.google.com/books?id=cdxWNE7NY6QC, retrieved 2021-10-31 , pp. 309–314.
  22. ↑ "The Nobel Prize in Physics 1921". Nobelprize.org. https://www.nobelprize.org/nobel_prizes/physics/laureates/1921/. 
  23. ↑ *Smith, Richard (1962). "Two Photon Photoelectric Effect". Physical Review 128 (5): 2225. doi:10.1103/PhysRev.128.2225. Bibcode: 1962PhRv..128.2225S. 
  24. ↑ 24.0 24.1 Heilbron, John L. (2013). "The path to the quantum atom". Nature 498 (7452): 27–30. doi:10.1038/498027a. PMID 23739408. 
  25. ↑ Nicholson, J. W. (1911). "The spectrum of Nebulium". Monthly Notices of the Royal Astronomical Society 72: 49. doi:10.1093/mnras/72.1.49. Bibcode: 1911MNRAS..72...49N. 
  26. ↑ *Nicholson, J. W. (1911). "The Constitution of the Solar Corona I". Monthly Notices of the Royal Astronomical Society 72: 139. doi:10.1093/mnras/72.2.139. Bibcode: 1911MNRAS..72..139N. 
    • Nicholson, J. W. (1912). "The Constitution of the Solar Corona II". Monthly Notices of the Royal Astronomical Society 72 (8): 677–693. doi:10.1093/mnras/72.8.677. 
    • Nicholson, J. W. (1912). "The Constitution of the Solar Corona III". Monthly Notices of the Royal Astronomical Society 72 (9): 729–740. doi:10.1093/mnras/72.9.729. 
  27. ↑ Nicholson, J. W. (1912). "On the new nebular line at λ4353". Monthly Notices of the Royal Astronomical Society 72 (8): 693. doi:10.1093/mnras/72.8.693. Bibcode: 1912MNRAS..72..693N. 
  28. ↑ 28.0 28.1 McCormmach, Russell (1966). "The Atomic Theory of John William Nicholson". Archive for History of Exact Sciences 3 (2): 160–184. doi:10.1007/BF00357268. 
  29. ↑ 29.0 29.1 Bohr, N. (1913). "On the constitution of atoms and molecules". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 6th series 26 (151): 1–25. doi:10.1080/14786441308634955. Bibcode: 1913PMag...26..476B. https://zenodo.org/record/2493915. Retrieved 2023-07-23. 
  30. ↑ Hirosige, Tetu; Nisio, Sigeko (1964). "Formation of Bohr's theory of atomic constitution". Japanese Studies in History of Science 3: 6–28. 
  31. ↑ J. L. Heilbron, A History of Atomic Models from the Discovery of the Electron to the Beginnings of Quantum Mechanics, diss. (University of California, Berkeley, 1964).
  32. ↑ Giuseppe Morandi; F. Napoli; E. Ercolessi (2001), Statistical mechanics: an intermediate course, World Scientific, p. 84, ISBN 978-981-02-4477-4, https://books.google.com/books?id=MhInFlnNsREC&pg=PA51, retrieved 2021-10-31 
  33. ↑ ter Haar, D. (1967). The Old Quantum Theory. Pergamon Press. p. 133. ISBN 978-0-08-012101-7. https://archive.org/details/oldquantumtheory0000haar. 
  34. ↑ Einstein, Albert (2003), "Physics and Reality", Daedalus 132 (4): 24, doi:10.1162/001152603771338742, http://www.kostic.niu.edu/Physics_and_RealityAlbert_Einstein.pdf, "The question is first: How can one assign a discrete succession of energy values Hσ to a system specified in the sense of classical mechanics (the energy function is a given function of the coordinates qr and the corresponding momenta pr)? The Planck constant h relates the frequency Hσ/h to the energy values Hσ. It is therefore sufficient to give to the system a succession of discrete frequency values." 
  35. ↑ International Bureau of Weights and Measures (2019-05-20), SI Brochure: The International System of Units (SI) (9th ed.), ISBN 978-92-822-2272-0, https://www.bipm.org/utils/common/pdf/si-brochure/SI-Brochure-9.pdf 
  36. ↑ "The Feynman Lectures on Physics Vol. II Ch. 19: The Principle of Least Action". https://www.feynmanlectures.caltech.edu/II_19.html. 
  37. ↑ "2018 CODATA Value: Avogadro constant". The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. http://physics.nist.gov/cgi-bin/cuu/Value?na. Retrieved 2019-05-20. 
  38. ↑ 38.0 38.1 "reduced Planck constant". NIST. 20 May 2019. https://physics.nist.gov/cgi-bin/cuu/Value?hbar. 
  39. ↑ Lyth, David H.; Liddle, Andrew R. (11 June 2009) (in en). The Primordial Density Perturbation: Cosmology, Inflation and the Origin of Structure. Cambridge University Press. ISBN 978-1-139-64374-0. https://books.google.com/books?id=IPwgAwAAQBAJ. 
  40. ↑ Huang, Kerson (26 April 2010) (in en). Quantum Field Theory: From Operators to Path Integrals. John Wiley & Sons. ISBN 978-3-527-40846-7. https://books.google.com/books?id=5ZWZRpvZzUEC. 
  41. ↑ Schmitz, Kenneth S. (11 November 2016) (in en). Physical Chemistry: Concepts and Theory. Elsevier. ISBN 978-0-12-800600-9. https://books.google.com/books?id=Y1ydBgAAQBAJ. 
  42. ↑ Chabay, Ruth W.; Sherwood, Bruce A. (20 November 2017) (in en). Matter and Interactions. John Wiley & Sons. ISBN 978-1-119-45575-2. https://books.google.com/books?id=zMWHEAAAQBAJ. 
  43. ↑ Schwarz, Patricia M.; Schwarz, John H. (25 March 2004) (in en). Special Relativity: From Einstein to Strings. Cambridge University Press. ISBN 978-1-139-44950-2. https://books.google.com/books?id=BmhQxWwk0K4C. 
  44. ↑ Lévy-Leblond, Jean-Marc (2002). "The meanings of Planck's constant" (in en). One Hundred Years of H: Pavia, 14-16 September 2000. Italian Physical Society. ISBN 978-88-7438-003-9. https://ssqg.ans.pw.edu.pl/en/wp-content/uploads/2021/04/JMLL_Meanings-of-h.pdf. 
  45. ↑ Shu, Frank (1982) (in en). The Physical Universe: An Introduction to Astronomy. University Science Books. ISBN 978-0-935702-05-7. https://books.google.com/books?id=v_6PbAfapSAC. 
  46. ↑ "Bohr Radius -- from Eric Weisstein's World of Physics" (in en). https://scienceworld.wolfram.com/physics/BohrRadius.html. 
  47. ↑ 47.0 47.1 Rennie, Richard; Law, Jonathan, eds (2017). "Planck constant". A Dictionary of Physics. Oxford Quick Reference (7th ed.). Oxford, UK: OUP Oxford. ISBN 978-0198821472. https://books.google.com/books?id=YPmFDwAAQBAJ. 
  48. ↑ (in en) The International Encyclopedia of Physical Chemistry and Chemical Physics. Pergamon Press. 1960. https://books.google.com/books?id=ufTvAAAAMAAJ. 
  49. ↑ Vértes, Attila; Nagy, Sándor; Klencsár, Zoltán; Lovas, Rezso György; Rösch, Frank (10 December 2010) (in en). Handbook of Nuclear Chemistry. Springer Science & Business Media. ISBN 978-1-4419-0719-6. https://books.google.com/books?id=NQyF6KaUScQC. 
  50. ↑ Bethe, Hans A.; Salpeter, Edwin E. (1957). "Quantum Mechanics of One- and Two-Electron Atoms" (in en). Handbuch der Physik: Atome I-II. Springer. https://books.google.com/books?id=A-APAQAAMAAJ. 
  51. ↑ Lang, Kenneth (11 November 2013) (in en). Astrophysical Formulae: A Compendium for the Physicist and Astrophysicist. Springer Science & Business Media. ISBN 978-3-662-11188-8. https://books.google.com/books?id=LyzrCAAAQBAJ. 
  52. ↑ Galgani, L.; Carati, A.; Pozzi, B. (December 2002). "The Problem of the Rate of Thermalization, and the Relations between Classical and Quantum Mechanics". Mathematical Models and Methods for Smart Materials, Cortona, Italy, 25 – 29 June 2001. pp. 111–122. doi:10.1142/9789812776273_0011. ISBN 978-981-238-235-1. 
  53. ↑ Fox, Mark (14 June 2018) (in en). A Student's Guide to Atomic Physics. Cambridge University Press. ISBN 978-1-316-99309-5. https://books.google.com/books?id=pVtlDwAAQBAJ. 
  54. ↑ Kleiss, Ronald (10 June 2021) (in en). Quantum Field Theory: A Diagrammatic Approach. Cambridge University Press. ISBN 978-1-108-78750-5. https://books.google.com/books?id=G_UvEAAAQBAJ. 
  55. ↑ Zohuri, Bahman (5 January 2021) (in en). Thermal Effects of High Power Laser Energy on Materials. Springer Nature. ISBN 978-3-030-63064-5. https://books.google.com/books?id=P3gSEAAAQBAJ. 
  56. ↑ Balian, Roger (26 June 2007) (in en). From Microphysics to Macrophysics: Methods and Applications of Statistical Physics. Volume II. Springer Science & Business Media. ISBN 978-3-540-45480-9. https://books.google.com/books?id=cUY_AAAAQBAJ. 
  57. ↑ Chen, C. Julian (15 August 2011) (in en). Physics of Solar Energy. John Wiley & Sons. ISBN 978-1-118-04459-9. https://books.google.com/books?id=dFKz6GwSVNEC. 
  58. ↑ "Dirac h". Britannica. https://www.britannica.com/science/Dirac-h. Retrieved 2023-09-27. 
  59. ↑ Shoenberg, D. (3 September 2009) (in en). Magnetic Oscillations in Metals. Cambridge University Press. ISBN 978-1-316-58317-3. https://books.google.com/books?id=HM_LCgAAQBAJ. 
  60. ↑ Powell, John L.; Crasemann, Bernd (5 May 2015) (in en). Quantum Mechanics. Courier Dover Publications. ISBN 978-0-486-80478-1. https://books.google.com/books?id=GHifCQAAQBAJ. 
  61. ↑ Dresden, Max (6 December 2012) (in en). H.A. Kramers Between Tradition and Revolution. Springer Science & Business Media. ISBN 978-1-4612-4622-0. https://books.google.com/books?id=1ggDCAAAQBAJ. 
  62. ↑ Johnson, R. E. (6 December 2012) (in en). Introduction to Atomic and Molecular Collisions. Springer Science & Business Media. ISBN 978-1-4684-8448-9. https://books.google.com/books?id=cKPTBwAAQBAJ. 
  63. ↑ Garcia, Alejandro; Henley, Ernest M. (13 July 2007) (in en). Subatomic Physics (3rd ed.). World Scientific Publishing Company. ISBN 978-981-310-167-8. https://books.google.com/books?id=j847DQAAQBAJ. 
  64. ↑ Holbrow, Charles H.; Lloyd, James N.; Amato, Joseph C.; Galvez, Enrique; Parks, M. Elizabeth (14 September 2010) (in en). Modern Introductory Physics. New York: Springer Science & Business Media. ISBN 978-0-387-79080-0. https://books.google.com/books?id=CYE_AAAAQBAJ. 
  65. ↑ Polyanin, Andrei D.; Chernoutsan, Alexei (18 October 2010) (in en). A Concise Handbook of Mathematics, Physics, and Engineering Sciences. CRC Press. ISBN 978-1-4398-0640-1. https://books.google.com/books?id=ejzScufwDRUC. 
  66. ↑ Dowling, Jonathan P. (24 August 2020) (in en). Schrödinger's Web: Race to Build the Quantum Internet. CRC Press. ISBN 978-1-000-08017-9. https://books.google.com/books?id=unP2DwAAQBAJ. 
  67. ↑ Landau, L. D.; Lifshitz, E. M. (22 October 2013) (in en). Quantum Mechanics: Non-Relativistic Theory. Elsevier. ISBN 978-1-4831-4912-7. https://books.google.com/books?id=neBbAwAAQBAJ. 
  68. ↑ Griffiths, David J.; Schroeter, Darrell F. (20 November 2019) (in en). Introduction to Quantum Mechanics. Cambridge University Press. ISBN 978-1-108-10314-5. https://books.google.com/books?id=zU3bDwAAQBAJ. 
  69. ↑ "Planck's constant". The Great Soviet Encyclopedia (1970-1979, 3rd ed.). The Gale Group. https://encyclopedia2.thefreedictionary.com/Planck%27s+constant. 
  70. ↑ Itzykson, Claude; Zuber, Jean-Bernard (20 September 2012) (in en). Quantum Field Theory. Courier Corporation. ISBN 978-0-486-13469-7. https://books.google.com/books?id=CxYCMNrUnTEC. 
  71. ↑ Kaku, Michio (1993) (in en). Quantum Field Theory: A Modern Introduction. Oxford University Press. ISBN 978-0-19-507652-3. https://books.google.com/books?id=6J7vAAAAMAAJ. 
  72. ↑ Bogoli︠u︡bov, Nikolaĭ Nikolaevich; Shirkov, Dmitriĭ Vasilʹevich (1982) (in en). Quantum Fields. Benjamin/Cummings Publishing Company, Advanced Book Program/World Science Division. ISBN 978-0-8053-0983-6. https://books.google.com/books?id=wczvAAAAMAAJ. 
  73. ↑ Aitchison, Ian J. R.; Hey, Anthony J. G. (17 December 2012) (in en). Gauge Theories in Particle Physics: A Practical Introduction: From Relativistic Quantum Mechanics to QED, Fourth Edition. CRC Press. ISBN 978-1-4665-1299-3. https://books.google.com/books?id=-v6sPfuyUt8C. 
  74. ↑ de Wit, B.; Smith, J. (2 December 2012) (in en). Field Theory in Particle Physics, Volume 1. Elsevier. ISBN 978-0-444-59622-2. https://books.google.com/books?id=cCAGmj6XEfkC. 
  75. ↑ Brown, Lowell S. (1992) (in en). Quantum Field Theory. Cambridge University Press. ISBN 978-0-521-46946-3. https://books.google.com/books?id=mKsRAVX1910C. 
  76. ↑ Buchbinder, Iosif L.; Shapiro, Ilya (March 2021) (in en). Introduction to Quantum Field Theory with Applications to Quantum Gravity. Oxford University Press. ISBN 978-0-19-883831-9. https://books.google.com/books?id=tL4cEAAAQBAJ. 
  77. ↑ "9. Where does quantum field theory fit into the big picture?" (in en). Conceptual Foundations of Quantum Field Theory. Cambridge University Press. 25 March 2004. ISBN 978-0-521-60272-3. https://books.google.com/books?id=d0wS0EJHZ3MC. 
  78. ↑ Cabibbo, Nicola; Maiani, Luciano; Benhar, Omar (28 July 2017) (in en). An Introduction to Gauge Theories. CRC Press. ISBN 978-1-4987-3452-3. https://books.google.com/books?id=6WxGDwAAQBAJ. 
  79. ↑ Casalbuoni, Roberto (6 April 2017) (in en). Introduction To Quantum Field Theory (Second ed.). World Scientific Publishing Company. ISBN 978-981-314-668-6. https://books.google.com/books?id=MFEyDwAAQBAJ. 
  80. ↑ Das, Ashok (24 July 2020) (in en). Lectures On Quantum Field Theory (2nd ed.). World Scientific. ISBN 978-981-12-2088-3. https://books.google.com/books?id=gXr1DwAAQBAJ. 
  81. ↑ Desai, Bipin R. (2010) (in en). Quantum Mechanics with Basic Field Theory. Cambridge University Press. ISBN 978-0-521-87760-2. https://books.google.com/books?id=cScBCJ6wLpYC. 
  82. ↑ Donoghue, John; Sorbo, Lorenzo (8 March 2022) (in en). A Prelude to Quantum Field Theory. Princeton University Press. ISBN 978-0-691-22348-3. https://books.google.com/books?id=Wv5FEAAAQBAJ. 
  83. ↑ Folland, Gerald B. (3 February 2021) (in en). Quantum Field Theory: A Tourist Guide for Mathematicians. American Mathematical Soc.. ISBN 978-1-4704-6483-7. https://books.google.com/books?id=nPEbEAAAQBAJ. 
  84. ↑ Fradkin, Eduardo (23 March 2021) (in en). Quantum Field Theory: An Integrated Approach. Princeton University Press. ISBN 978-0-691-14908-0. https://books.google.com/books?id=ruEIEAAAQBAJ. 
  85. ↑ Gelis, François (11 July 2019) (in en). Quantum Field Theory. Cambridge University Press. ISBN 978-1-108-48090-1. https://books.google.com/books?id=BzGdDwAAQBAJ. 
  86. ↑ Greiner, Walter; Reinhardt, Joachim (9 March 2013) (in en). Quantum Electrodynamics. Springer Science & Business Media. ISBN 978-3-662-05246-4. https://books.google.com/books?id=6y3rCAAAQBAJ. 
  87. ↑ Liboff, Richard L. (2003) (in en). Introductory Quantum Mechanics (4th ed.). San Francisco: Pearson Education. ISBN 978-81-317-0441-7. https://books.google.com/books?id=xMIlAgQSRUsC. 
  88. ↑ Barut, A. O. (1 August 1978). "The Creation of a Photon: A Heuristic Calculation of Planck's Constant ħ or the Fine Structure Constant α". Zeitschrift für Naturforschung A 33 (8): 993–994. doi:10.1515/zna-1978-0819. Bibcode: 1978ZNatA..33..993B. 
  89. ↑ Kocia, Lucas; Love, Peter (12 July 2018). "Measurement contextuality and Planck's constant". New Journal of Physics 20 (7): 073020. doi:10.1088/1367-2630/aacef2. Bibcode: 2018NJPh...20g3020K. 
  90. ↑ Humpherys, David (28 November 2022). "The Implicit Structure of Planck's Constant". European Journal of Applied Physics 4 (6): 22–25. doi:10.24018/ejphysics.2022.4.6.227. 
  91. ↑ Bais, F. Alexander; Farmer, J. Doyne (2008). "The Physics of Information". in Adriaans, Pieter. Philosophy of Information. Handbook of the Philosophy of Science. 8. Amsterdam: North-Holland. ISBN 978-0-444-51726-5. https://www.sciencedirect.com/science/article/abs/pii/B9780444517265500200. 
  92. ↑ Hirota, E.; Sakakima, H.; Inomata, K. (9 March 2013) (in en). Giant Magneto-Resistance Devices. Springer Science & Business Media. ISBN 978-3-662-04777-4. https://books.google.com/books?id=mvDrCAAAQBAJ. 
  93. ↑ Gardner, John H. (1988). "An Invariance Theory". Encyclia 65: 139. 
  94. ↑ Levine, Raphael D. (4 June 2009) (in en). Molecular Reaction Dynamics. Cambridge University Press. ISBN 978-1-139-44287-9. https://books.google.com/books?id=FVqyS31OM7sC. 
  95. ↑ Heilbron, John L. (June 2013). "The path to the quantum atom". Nature 498 (7452): 27–30. doi:10.1038/498027a. PMID 23739408. 
  96. ↑ McCormmach, Russell (1 January 1966). "The atomic theory of John William Nicholson". Archive for History of Exact Sciences 3 (2): 160–184. doi:10.1007/BF00357268. 
  97. ↑ 97.0 97.1 Mehra, Jagdish; Rechenberg, Helmut (3 August 1982) (in en). The Historical Development of Quantum Theory. 1. Springer New York. ISBN 978-0-387-90642-3. https://books.google.com/books?id=oLWNzwEACAAJ. 
  98. ↑ 98.0 98.1 98.2 Nicholson, J. W. (14 June 1912). "The Constitution of the Solar Corona. II.". Monthly Notices of the Royal Astronomical Society (Oxford University Press) 72 (8): 677–693. doi:10.1093/mnras/72.8.677. ISSN 0035-8711. 
  99. ↑ 99.0 99.1 Bohr, N. (July 1913). "I. On the constitution of atoms and molecules". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 26 (151): 1–25. doi:10.1080/14786441308634955. https://zenodo.org/record/2493915. 
  100. ↑ Wilson, W. (1956). "John William Nicholson 1881-1955". Biographical Memoirs of Fellows of the Royal Society 2: 209–214. doi:10.1098/rsbm.1956.0014. 
  101. ↑ Sommerfeld, A. (1915). "Zur Theorie der Balmerschen Serie". Sitzungsberichte der mathematisch-physikalischen Klasse der K. B. Akademie der Wissenschaften zu München 33 (198): 425–458. doi:10.1140/epjh/e2013-40053-8. https://static-content.springer.com/esm/art%3A10.1140%2Fepjh%2Fe2013-40053-8/MediaObjects/13129_2013_121_MOESM1_ESM.pdf. 
  102. ↑ Schwarzschild, K. (1916). "Zur Quantenhypothese". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin: 548–568. 
  103. ↑ Ehrenfest, P. (June 1917). "XLVIII. Adiabatic invariants and the theory of quanta". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 33 (198): 500–513. doi:10.1080/14786440608635664. 
  104. ↑ Landé, A. (June 1919). "Das Serienspektrum des Heliums". Physikalische Zeitschrift 20: 228–234. 
  105. ↑ Bohr, N. (October 1920). "Über die Serienspektra der Elemente". Zeitschrift für Physik 2 (5): 423–469. doi:10.1007/BF01329978. 
  106. ↑ Stern, Otto (December 1921). "Ein Weg zur experimentellen Prüfung der Richtungsquantelung im Magnetfeld". Zeitschrift für Physik 7 (1): 249–253. doi:10.1007/BF01332793. https://books.google.com/books?id=hlZKAAAAMAAJ&dq=%22Ein+Weg+zur+experimentellen+Pr%C3%BCfung+der+Richtungsquantelung%22+%22Bringen+wir+also+ein+Gas+aus+Atomen%22&pg=PA249. 
  107. ↑ Heisenberg, Werner (December 1922). "Zur Quantentheorie der Linienstruktur und der anomalen Zeemaneflekte". Zeitschrift für Physik 8 (1): 273–297. doi:10.1007/BF01329602. 
  108. ↑ Kramers, H. A.; Pauli, W. (December 1923). "Zur Theorie der Bandenspektren". Zeitschrift für Physik 13 (1): 351–367. doi:10.1007/BF01328226. https://books.google.com/books?id=9PpMAQAAIAAJ&dq=%22negativen+Halogenionen+ein+resultierendes%22&pg=RA1-PA351. 
  109. ↑ Born, M.; Jordan, P. (December 1925). "Zur Quantenmechanik". Zeitschrift für Physik 34 (1): 858–888. doi:10.1007/BF01328531. 
  110. ↑ Dirac, P. A. M. (December 1925). "The fundamental equations of quantum mechanics". Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 109 (752): 642–653. doi:10.1098/rspa.1925.0150. 
  111. ↑ Born, M.; Heisenberg, W.; Jordan, P. (August 1926). "Zur Quantenmechanik. II.". Zeitschrift für Physik 35 (8–9): 557–615. doi:10.1007/BF01379806. 
  112. ↑ Schrödinger, E. (1926). "Quantisierung als Eigenwertproblem". Annalen der Physik 384 (4): 361–376. doi:10.1002/andp.19263840404. 
  113. ↑ Dirac, P. A. M. (October 1926). "On the theory of quantum mechanics". Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 112 (762): 661–677. doi:10.1098/rspa.1926.0133. 
  114. ↑ 114.0 114.1 Mehra, Jagdish; Rechenberg, Helmut (2000) (in en). The Historical Development of Quantum Theory. 6. New York: Springer. 
  115. ↑ Dirac, P. A. M. (1930). The Principles of Quantum Mechanics (1st ed.). Oxford, U.K.: Clarendon. 

Sources

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Planck_constant&oldid=3284389"