FIR transfer function
Transfer function filter utilizes the transfer function and the Convolution theorem to produce a filter. In this article, an example of such a filter using finite impulse response is discussed and an application of the filter into real world data is shown.
FIR (Finite Impulse Response) Linear filters
In digital processing, an FIR filter is a time-continuous filter that is invariant with time. This means that the filter does not depend on the specific point of time, but rather depends on the time duration. The specification of this filter uses a transfer function which has a frequency response which will only pass the desired frequencies of the input. This type of filter is non-recursive, which means that the output can be completely derived at from a combination of the input without any recursive values of the output. This means that there is no feedback loop that feeds the new output the values of previous outputs. This is an advantage over recursive filters such as IIR filter (Infinite Impulse Response) in the applications that require a linear phase response because it will pass the input without a phase distortion.[1]
Mathematical model
Let the output function be [math]\displaystyle{ y(t) }[/math] and the input is [math]\displaystyle{ x(t) }[/math]. The convolution of the input with a transfer function [math]\displaystyle{ h(t) }[/math] provides a filtered output. The mathematical model of this type of filter is:
- [math]\displaystyle{ y(t) = \int_{0}^{T} x(t-\tau)\, h(\tau)\, d\tau }[/math]
h([math]\displaystyle{ \tau }[/math]) is a transfer function of an impulse response to the input. The convolution allows the filter to only be activated when the input recorded a signal at the same time value. This filter returns the input values (x(t)) if k falls into the support region of function h. This is the reason why this filter is called finite response. If k is outside of the support region, the impulse response is zero which makes output zero. The central idea of this h([math]\displaystyle{ \tau }[/math]) function can be thought of as a quotient of two functions.[2]
According to Huang (1981)[3] Using this mathematical model, there are four methods of designing non-recursive linear filters with various concurrent filter designs:
- Window design method
- Frequency Sampling method
- Conventional linear programming
- Iterative linear programming
Single-sided Linear Filter
Input function
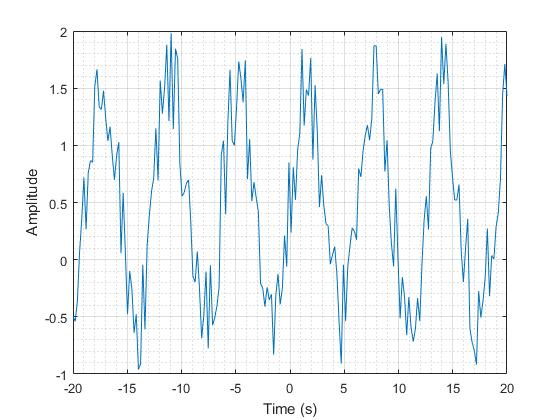
Define the input signal:
- [math]\displaystyle{ y(t) = \sin(t) + rand(\begin{bmatrix}1 & 200\end{bmatrix}) }[/math]
[math]\displaystyle{ rand(\begin{bmatrix}1 & 200\end{bmatrix}) }[/math] adds a random number from 1 to 200 to the sinusoidal function which serves to distort the data.
Single-sided filter
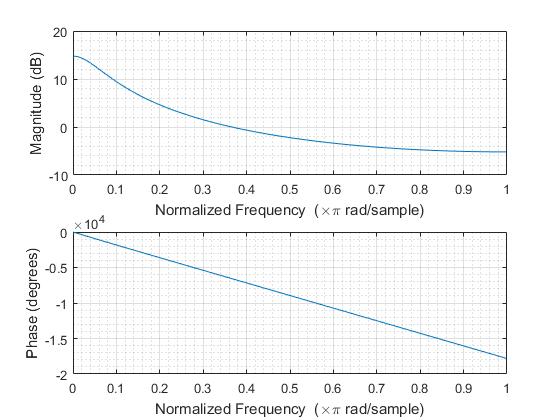
Use an exponential function as the impulse response for the support region of positive values.
- [math]\displaystyle{ h(t) = \begin{cases} 0, & \forall &-\infty &\le & t &\le 0 \\ e^{-t}, \quad & \forall &0 &\le & t &\le +\infty \end{cases} }[/math]
The frequency response of this filter resembles a low-pass filter as in the lower frequency.
Double-sided filter
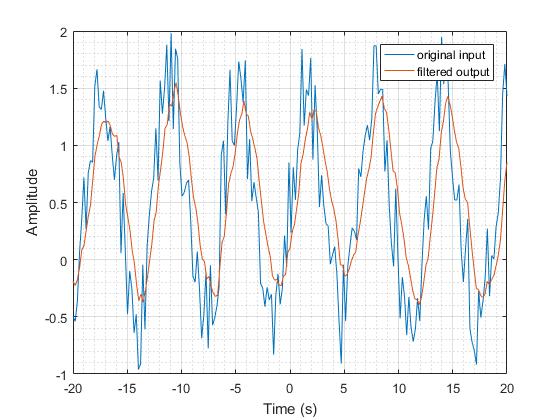
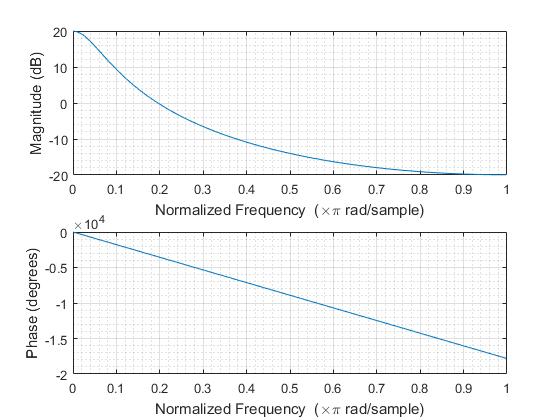
Let the input signal to be the same as the single-sided function. Use an exponential function as the impulse response for the support region of positive values as before. In this double-sided filter, also implement another exponential function. The opposite in signs of the powers of the exponent is to maintain the non-infinite results when computing the exponential functions.
[math]\displaystyle{ h(t) = \begin{cases} e^{t}, & \forall & -\infty &\le & t &\le 0 \\ e^{-t}, &\forall & 0 &\le &t &\le +\infty \end{cases} }[/math]
Examine this filter in its frequency domain, we see that the magnitude response is the same trend as the single sided filter. However, the frequencies that can be passed are smaller than those of the single-sided filter. This resulted in a smoother output. The significant of this consequence is that the double-sided filters types of linear filters are better being a filter.
FIR Transfer function Linear filter Application
Linear filter performs better when it is a double-sided filter. This requires the data to be known in advance which makes it a challenge for these filters to function well in situations where signals cannot be known ahead of time such as radio signal processing. However, this means that linear filters are extremely useful in filtering pre-loaded data. In addition, because of its non-recursive nature which preserves the phase angles of the input, linear filters are usually used in image processing, video processing, data processing or pattern detection. Some examples are image enhancement, restoration and pre-whitening for spectral analysis.[4] Additionally, linear non-recursive filters are always stable and usually produce a purely real output which makes them more favorable. They are also computationally easy which usually creates a big advantage for using this FIR linear filter.
References
- ↑ IIR Filters and FIR Filters. (2012, June). Retrieved May 04, 2017, from http://zone.ni.com/reference/en-XX/help/370858K-01/genmaths/genmaths/calc_filterfir_iir/
- ↑ Nagai, N. (1990). Linear circuits, systems, and signal processing: Advanced theory and applications. New York: M. Dekker.
- ↑ Huang, T. S. (1981). Topics in applied physics: Two-Dimensional Digital Signal Processing I (3rd ed., Vol. 42, Topics in Applied Physics). Berlin: Springer.
- ↑ Huang, T. S. (1981). Topics in applied physics: Two-Dimensional Digital Signal Processing I (3rd ed., Vol. 42, Topics in Applied Physics). Berlin: Springer.
 |