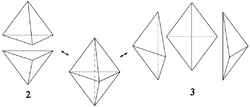
Pachner moves
In topology, a branch of mathematics, Pachner moves, named after Udo Pachner, are ways of replacing a triangulation of a piecewise linear manifold by a different triangulation of a homeomorphic manifold. Pachner moves are also called bistellar flips. Any two triangulations of a piecewise linear manifold are related by a finite sequence of Pachner moves.
Definition
Let [math]\displaystyle{ \Delta_{n+1} }[/math] be the [math]\displaystyle{ (n+1) }[/math]-simplex. [math]\displaystyle{ \partial \Delta_{n+1} }[/math] is a combinatorial n-sphere with its triangulation as the boundary of the n+1-simplex.
Given a triangulated piecewise linear (PL) n-manifold [math]\displaystyle{ N }[/math], and a co-dimension 0 subcomplex [math]\displaystyle{ C \subset N }[/math] together with a simplicial isomorphism [math]\displaystyle{ \phi : C \to C' \subset \partial \Delta_{n+1} }[/math], the Pachner move on N associated to C is the triangulated manifold [math]\displaystyle{ (N \setminus C) \cup_\phi (\partial \Delta_{n+1} \setminus C') }[/math]. By design, this manifold is PL-isomorphic to [math]\displaystyle{ N }[/math] but the isomorphism does not preserve the triangulation.
See also
References
- Pachner, Udo (1991), "P.L. homeomorphic manifolds are equivalent by elementary shellings", European Journal of Combinatorics 12 (2): 129–145, doi:10.1016/s0195-6698(13)80080-7.
 |