Lyapunov–Malkin theorem
The Lyapunov–Malkin theorem (named for Aleksandr Lyapunov and Ioel Malkin (ru)) is a mathematical theorem detailing stability of nonlinear systems.[1][2]
Theorem
In the system of differential equations,
- [math]\displaystyle{ \dot x = Ax + X(x,y),\quad\dot y = Y(x,y) }[/math]
where [math]\displaystyle{ x \in \mathbb{R}^m }[/math] and [math]\displaystyle{ y \in \mathbb{R}^n }[/math] are components of the system state, [math]\displaystyle{ A \in \mathbb{R}^{m\times m} }[/math] is a matrix that represents the linear dynamics of [math]\displaystyle{ x }[/math], and [math]\displaystyle{ X : \mathbb{R}^m\times \mathbb{R}^n \to \mathbb{R}^m }[/math] and [math]\displaystyle{ Y : \mathbb{R}^m\times \mathbb{R}^n \to \mathbb{R}^n }[/math] represent higher-order nonlinear terms. If all eigenvalues of the matrix [math]\displaystyle{ A }[/math] have negative real parts, and X(x, y), Y(x, y) vanish when x = 0, then the solution x = 0, y = 0 of this system is stable with respect to (x, y) and asymptotically stable with respect to x. If a solution (x(t), y(t)) is close enough to the solution x = 0, y = 0, then
- [math]\displaystyle{ \lim_{t \to \infty}x(t) = 0,\quad \lim_{t \to \infty}y(t) = c. }[/math]
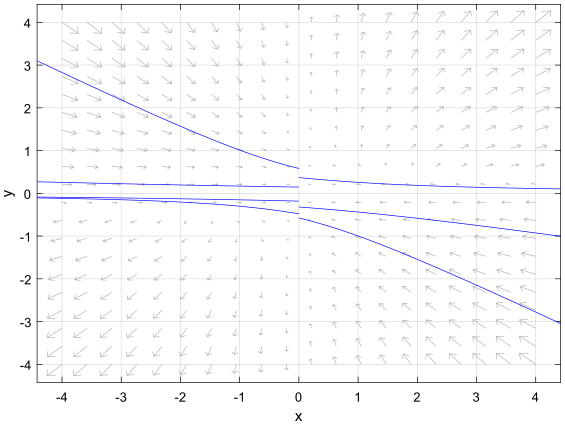
Example
Consider the vector field given by
[math]\displaystyle{ \dot x = -x + x^2y, \quad\dot y = xy^2 }[/math]
In this case, A = -1 and X(0, y) = Y(0, y) = 0 for all y, so this system satisfy the hypothesis of Lyapunov-Malkin theorem.
The figure below shows a plot of this vector field along with some trajectories that pass near (0,0). As expected by the theorem, it can be seen that trajectories in the neighborhood of (0,0) converges to a point in the form (0,c).
References
- ↑ Zenkov, D. V.; Bloch, A. M.; Marsden, J. E. (2002). "Lyapunov–Malkin Theorem and Stabilization of the Unicycle Rider". Systems and Control Letters 45 (4): 293–302. doi:10.1016/S0167-6911(01)00187-6. https://authors.library.caltech.edu/20025/1/ZeBlMa2002.pdf.
- ↑ Bloch, Anthony; Krishnaprasad, Perinkulam Sambamurthy; Murray, R. M. (2015). Nonholonomic mechanics and control (2nd ed.). New York, NY. ISBN 9781493930173. OCLC 932167031.
 |