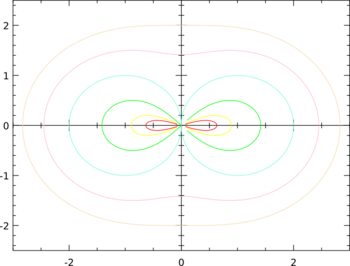
Hippopede
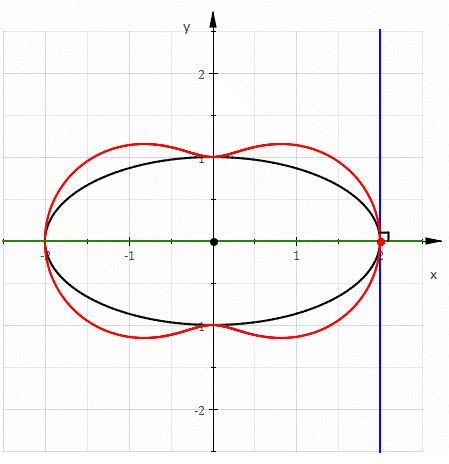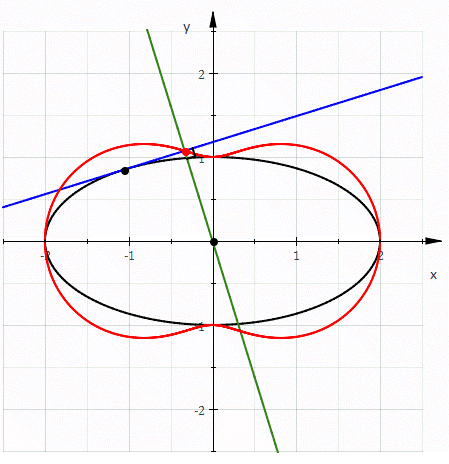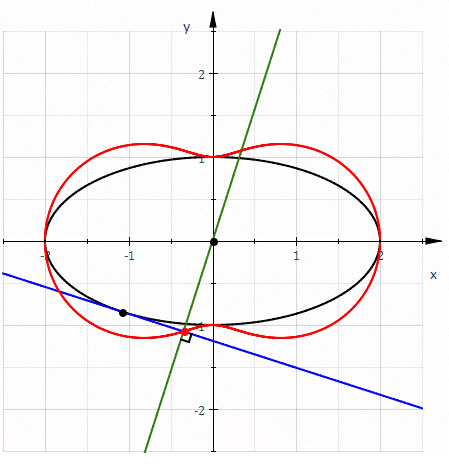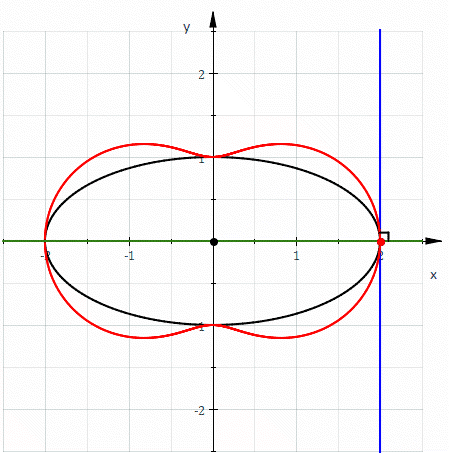
In geometry, a hippopede (from grc ἱπποπέδη (hippopédē) 'horse fetter') is a plane curve determined by an equation of the form
- [math]\displaystyle{ (x^2+y^2)^2=cx^2+dy^2, }[/math]
where it is assumed that c > 0 and c > d since the remaining cases either reduce to a single point or can be put into the given form with a rotation. Hippopedes are bicircular, rational, algebraic curves of degree 4 and symmetric with respect to both the x and y axes.
Special cases
When d > 0 the curve has an oval form and is often known as an oval of Booth, and when d < 0 the curve resembles a sideways figure eight, or lemniscate, and is often known as a lemniscate of Booth, after 19th-century mathematician James Booth who studied them. Hippopedes were also investigated by Proclus (for whom they are sometimes called Hippopedes of Proclus) and Eudoxus. For d = −c, the hippopede corresponds to the lemniscate of Bernoulli.
Definition as spiric sections
Hippopedes can be defined as the curve formed by the intersection of a torus and a plane, where the plane is parallel to the axis of the torus and tangent to it on the interior circle. Thus it is a spiric section which in turn is a type of toric section.
If a circle with radius a is rotated about an axis at distance b from its center, then the equation of the resulting hippopede in polar coordinates
- [math]\displaystyle{ r^2 = 4 b (a - b \sin^{2}\! \theta) }[/math]
or in Cartesian coordinates
- [math]\displaystyle{ (x^2+y^2)^2+4b(b-a)(x^2+y^2)=4b^2x^2 }[/math].
Note that when a > b the torus intersects itself, so it does not resemble the usual picture of a torus.
See also
References
- Lawrence JD. (1972) Catalog of Special Plane Curves, Dover Publications. Pp. 145–146.
- Booth J. A Treatise on Some New Geometrical Methods, Longmans, Green, Reader, and Dyer, London, Vol. I (1873) and Vol. II (1877).
- Weisstein, Eric W.. "Hippopede". http://mathworld.wolfram.com/Hippopede.html.
- "Hippopede" at 2dcurves.com
- "Courbes de Booth" at Encyclopédie des Formes Mathématiques Remarquables
External links
 |