Stuttering equivalence
In theoretical computer science, stuttering equivalence,[1] a relation written as
- [math]\displaystyle{ \pi\sim_{st}\pi' }[/math],
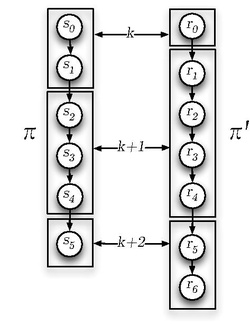
can be seen as a partitioning of paths [math]\displaystyle{ \pi }[/math] and [math]\displaystyle{ \pi' }[/math] into blocks, so that states in the [math]\displaystyle{ k^{\mathrm{th}} }[/math] block of one path are labeled ([math]\displaystyle{ L(\sdot) }[/math]) the same as states in the [math]\displaystyle{ k^{\mathrm{th}} }[/math] block of the other path. Corresponding blocks may have different lengths.
Formally, this can be expressed as two infinite paths [math]\displaystyle{ \pi=s_0, s_1, \ldots }[/math] and [math]\displaystyle{ \pi'=r_0, r_1, \ldots }[/math] being stuttering equivalent ([math]\displaystyle{ \pi \sim_{st} \pi' }[/math]) if there are two infinite sequences of integers [math]\displaystyle{ 0 = i_0 \lt i_1 \lt i_2 \lt \ldots }[/math] and [math]\displaystyle{ 0 = j_0 \lt j_1 \lt j_2 \lt \ldots }[/math] such that for every block [math]\displaystyle{ k \geq 0 }[/math] holds [math]\displaystyle{ L(s_{i_k}) = L(s_{i_k+1}) = \ldots = L(s_{i_{k+1}-1}) = L(r_{j_k}) = L(r_{j_k+1}) = \ldots = L(r_{j_{k+1}-1}) }[/math].
Stuttering equivalence is not the same as bisimulation, since bisimulation cannot capture the semantics of the 'eventually' (or 'finally') operator found in linear temporal/computation tree logic (branching time logic)(modal logic). So-called branching bisimulation has to be used.[citation needed]
References
- ↑ Groote, Jan Friso; Vaandrager, Frits W. (1990). "An efficient algorithm for branching bisimulation and stuttering equivalence". in Paterson, Michael S.. Proceedings of the 17th International Colloquium on Automata, Languages and Programming. Lecture Notes in Computer Science. 443. Springer-Verlag. pp. 626–638. doi:10.1007/BFb0032063. ISBN 0-387-52826-1. https://archive.org/details/automatalanguage0000ical/page/626.
 |