Alpha-beta model

The alpha-beta model is a mathematical equation used to describe the velocity of fatigue crack growth, da / dN, as a function of a constant amplitude load driving force ΔK where its constants α and β are obtained through a semi-empirical process. Originally the alpha-beta model was developed and tested from data generated in tests using commercial grade Titanium and Aluminium Alloy 2524-T3 both the structural materials of great interest aeronautical. This model is applied in two situations: the individual that conforms to the experimental data of a single test and can be compared to Paris' law; and the generalized one that tries to represent in a bi-parametric way the effects of R - ratio between the tensions intensity, minimum and maximum - for a set of tests in the same material.

In addition to the ease of application, the alpha-beta model allows precise adjustment of the experimental points that do not follow the linearity in region II proposed by the Paris' law, since it is known that some ductile materials and some metallic alloy have these linearity deviations. The alpha-beta model is given by the following equation:

[math]\displaystyle{ \frac{da}{dN}=e^\tfrac{Y}{\Delta K} }[/math]

Where, da / dN is the fatigue crack growth rate given in units of length per number of cycles. ΔK is the stress intensity factor and the Y parameter is the product between log of the crack propagation rate and the amplitude of the stress intensity factor, as follows:

[math]\displaystyle{ Y=ln\frac{da}{dN}\cdot\Delta K }[/math]

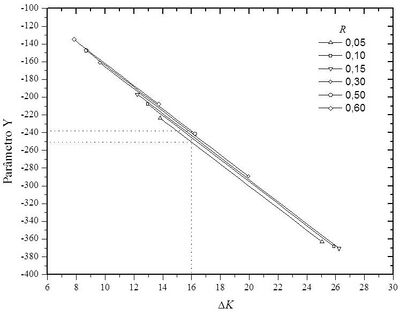
Representing in a graph Y (ΔK) for any value of R the result obtained is exactly a decreasing straight line, as shown in the figure below:

Then Y varies linearly as a function of ΔK and therefore can be written by a line equation:

[math]\displaystyle{ Y=\alpha\Delta K+\beta }[/math]

Where the values of the constants α and β are respectively the angular and linear coefficients of the line.

Individual alpha-beta model

The substitution of Y in the alpha-beta model gives rise to the individual model, used to calculate a single experiment, represented by:

[math]\displaystyle{ \frac{da}{dN}=e^\alpha \cdot e^\tfrac{\beta}{\Delta K} }[/math]

The constants α and β are calculated from experimental data concerning the assay to be described. In the interval 0 <da / dN <1, they always assume negative values.

Generalized alpha-beta model

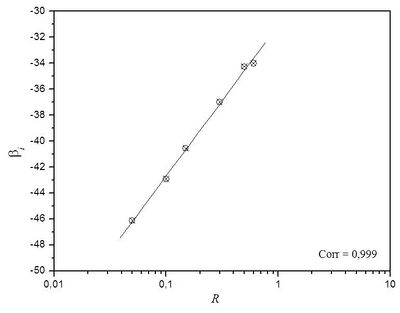
Since the curves of Y (ΔK) behave like parallel lines, this means that a single angular coefficient can be adopted for all the tests. If α is a single value for all the tests it is characterized that the constant β is responsible for the representation of the effect of R. The investigation of the constant β described as a function of R leads to a linear adjustment as in the figure below:

[math]\displaystyle{ \beta=\delta\log(R)+\gamma }[/math]

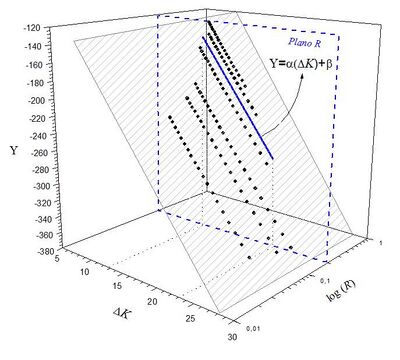
The substitution of β into Y gives rise to what represents the equation of a bi-parametric plane shown in the below, where this plane is formed from the experimental data.

[math]\displaystyle{ Y=\alpha\Delta K+\delta\log(R)+\gamma }[/math]

The coefficients α, δ, γ are easily found from the experimental data by the mathematical method of first order linear regression in space R ³ known as least squares method. Substituting the β equation into the Individual Alpha-Beta Model gives the equation of the generalized bi-parametric model.

[math]\displaystyle{ \frac{da}{dN}=e^\alpha \cdot e^\tfrac{\delta\log(R)+\gamma}{\Delta K} }[/math]

The generalized Alpha-Beta Model is represented by the bi-parametric form, because it describes the fatigue crack growth for a group of tests carried out on the same material (family of curves) as a function of two loading parameters, ΔK and R.