Six exponentials theorem
In mathematics, specifically transcendental number theory, the six exponentials theorem is a result that, given the right conditions on the exponents, guarantees the transcendence of at least one of a set of exponentials.
Statement
If x1, x2, ..., xd are d complex numbers that are linearly independent over the rational numbers, and y1, y2, ..., yl are l complex numbers that are also linearly independent over the rational numbers, and if dl > d + l, then at least one of the following dl numbers is transcendental:
- [math]\displaystyle{ \exp(x_i y_j),\quad (1 \leq i \leq d,\ 1 \leq j \leq l). }[/math]
The most interesting case is when d = 3 and l = 2, in which case there are six exponentials, hence the name of the result. The theorem is weaker than the related but thus far unproved four exponentials conjecture, whereby the strict inequality dl > d + l is replaced with dl ≥ d + l, thus allowing d = l = 2.
The theorem can be stated in terms of logarithms by introducing the set L of logarithms of algebraic numbers:
- [math]\displaystyle{ \mathcal{L}=\{\lambda\in\mathbb{C}\,:\,e^\lambda\in\overline{\mathbb{Q}}\}. }[/math]
The theorem then says that if λij are elements of L for i = 1, 2 and j = 1, 2, 3, such that λ11, λ12, and λ13 are linearly independent over the rational numbers, and λ11 and λ21 are also linearly independent over the rational numbers, then the matrix
- [math]\displaystyle{ M=\begin{pmatrix}\lambda_{11}&\lambda_{12}&\lambda_{13} \\ \lambda_{21}&\lambda_{22}&\lambda_{23}\end{pmatrix} }[/math]
has rank 2.
History
A special case of the result where x1, x2, and x3 are logarithms of positive integers, y1 = 1, and y2 is real, was first mentioned in a paper by Leonidas Alaoglu and Paul Erdős from 1944 in which they try to prove that the ratio of consecutive colossally abundant numbers is always prime. They claimed that Carl Ludwig Siegel knew of a proof of this special case, but it is not recorded.[1] Using the special case they manage to prove that the ratio of consecutive colossally abundant numbers is always either a prime or a semiprime.
The theorem was first explicitly stated and proved in its complete form independently by Serge Lang[2] and Kanakanahalli Ramachandra[3] in the 1960s.
Five exponentials theorem
A stronger, related result is the five exponentials theorem,[4] which is as follows. Let x1, x2 and y1, y2 be two pairs of complex numbers, with each pair being linearly independent over the rational numbers, and let γ be a non-zero algebraic number. Then at least one of the following five numbers is transcendental:
- [math]\displaystyle{ e^{x_1 y_1}, e^{x_1 y_2}, e^{x_2 y_1}, e^{x_2 y_2}, e^{\gamma x_2/x_1}. }[/math]
This theorem implies the six exponentials theorem and in turn is implied by the as yet unproven four exponentials conjecture, which says that in fact one of the first four numbers on this list must be transcendental.
Sharp six exponentials theorem
Another related result that implies both the six exponentials theorem and the five exponentials theorem is the sharp six exponentials theorem.[5] This theorem is as follows. Let x1, x2, and x3 be complex numbers that are linearly independent over the rational numbers, and let y1 and y2 be a pair of complex numbers that are linearly independent over the rational numbers, and suppose that βij are six algebraic numbers for 1 ≤ i ≤ 3 and 1 ≤ j ≤ 2 such that the following six numbers are algebraic:
- [math]\displaystyle{ e^{x_1 y_1-\beta_{11}}, e^{x_1 y_2-\beta_{12}}, e^{x_2 y_1-\beta_{21}}, e^{x_2 y_2-\beta_{22}}, e^{x_3 y_1-\beta_{31}}, e^{x_3 y_2-\beta_{32}}. }[/math]
Then xi yj = βij for 1 ≤ i ≤ 3 and 1 ≤ j ≤ 2. The six exponentials theorem then follows by setting βij = 0 for every i and j, while the five exponentials theorem follows by setting x3 = γ/x1 and using Baker's theorem to ensure that the xi are linearly independent.
There is a sharp version of the five exponentials theorem as well, although it as yet unproven so is known as the sharp five exponentials conjecture.[6] This conjecture implies both the sharp six exponentials theorem and the five exponentials theorem, and is stated as follows. Let x1, x2 and y1, y2 be two pairs of complex numbers, with each pair being linearly independent over the rational numbers, and let α, β11, β12, β21, β22, and γ be six algebraic numbers with γ ≠ 0 such that the following five numbers are algebraic:
- [math]\displaystyle{ e^{x_1 y_1-\beta_{11}}, e^{x_1 y_2-\beta_{12}}, e^{x_2 y_1-\beta_{21}}, e^{x_2 y_2-\beta_{22}}, e^{(\gamma x_2/x_1)-\alpha}. }[/math]
Then xi yj = βij for 1 ≤ i, j ≤ 2 and γx2 = αx1.
A consequence of this conjecture that isn't currently known would be the transcendence of eπ², by setting x1 = y1 = β11 = 1, x2 = y2 = iπ, and all the other values in the statement to be zero.
Strong six exponentials theorem
A further strengthening of the theorems and conjectures in this area are the strong versions. The strong six exponentials theorem is a result proved by Damien Roy that implies the sharp six exponentials theorem.[7] This result concerns the vector space over the algebraic numbers generated by 1 and all logarithms of algebraic numbers, denoted here as L∗. So L∗ is the set of all complex numbers of the form
- [math]\displaystyle{ \beta_0+\sum_{i=1}^n \beta_i\log\alpha_i, }[/math]
for some n ≥ 0, where all the βi and αi are algebraic and every branch of the logarithm is considered. The strong six exponentials theorem then says that if x1, x2, and x3 are complex numbers that are linearly independent over the algebraic numbers, and if y1 and y2 are a pair of complex numbers that are also linearly independent over the algebraic numbers then at least one of the six numbers xi yj for 1 ≤ i ≤ 3 and 1 ≤ j ≤ 2 is not in L∗. This is stronger than the standard six exponentials theorem which says that one of these six numbers is not simply the logarithm of an algebraic number.
There is also a strong five exponentials conjecture formulated by Michel Waldschmidt.[8] It would imply both the strong six exponentials theorem and the sharp five exponentials conjecture. This conjecture claims that if x1, x2 and y1, y2 are two pairs of complex numbers, with each pair being linearly independent over the algebraic numbers, then at least one of the following five numbers is not in L∗:
- [math]\displaystyle{ x_1y_1,\,x_1y_2,\,x_2y_1,\,x_2y_2,\,x_1/x_2. }[/math]
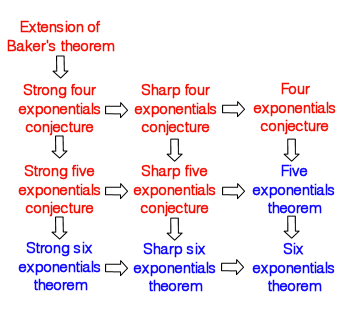
All the above conjectures and theorems are consequences of the unproven extension of Baker's theorem, that logarithms of algebraic numbers that are linearly independent over the rational numbers are automatically algebraically independent too. The diagram on the right shows the logical implications between all these results.
Generalization to commutative group varieties
The exponential function ez uniformizes the exponential map of the multiplicative group Gm. Therefore, we can reformulate the six exponential theorem more abstractly as follows:
- Let G = Gm × Gm and take u : C → G(C) to be a non-zero complex-analytic group homomorphism. Define L to be the set of complex numbers l for which u(l) is an algebraic point of G. If a minimal generating set of L over Q has more than two elements then the image u(C) is an algebraic subgroup of G(C).
(In order to derive the classical statement, set u(z) = (ey1z; ey2z) and note that Qx1 + Qx2 + Qx3 is a subset of L).
In this way, the statement of the six exponentials theorem can be generalized to an arbitrary commutative group variety G over the field of algebraic numbers. This generalized six exponential conjecture, however, seems out of scope at the current state of transcendental number theory.
For the special but interesting cases G = Gm × E and G = E × E′, where E, E′ are elliptic curves over the field of algebraic numbers, results towards the generalized six exponential conjecture were proven by Aleksander Momot.[9] These results involve the exponential function ez and a Weierstrass function [math]\displaystyle{ \wp }[/math] resp. two Weierstrass functions [math]\displaystyle{ \wp, \wp' }[/math] with algebraic invariants [math]\displaystyle{ g_2, g_3, g_2', g_3' }[/math], instead of the two exponential functions [math]\displaystyle{ e^{y_1z}, e^{y_2z} }[/math] in the classical statement.
Let G = Gm × E and suppose E is not isogenous to a curve over a real field and that u(C) is not an algebraic subgroup of G(C). Then L is generated over Q either by two elements x1, x2, or three elements x1, x2, x3 which are not all contained in a real line Rc, where c is a non-zero complex number. A similar result is shown for G = E × E′.[10]
Notes
- ↑ Alaoglu and Erdős, (1944), p.455: "Professor Siegel has communicated to us the result that q x, r x and s x can not be simultaneously rational except if x is an integer."
- ↑ Lang, (1966), chapter 2, section 1.
- ↑ Ramachandra, (1967/68).
- ↑ Waldschmidt, (1988), corollary 2.2.
- ↑ Waldschmidt, (2005), theorem 1.4.
- ↑ Waldschmidt, (2005), conjecture 1.5
- ↑ Roy, (1992), section 4, corollary 2.
- ↑ Waldschmidt, (1988).
- ↑ Momot, ch. 7
- ↑ Momot, ch. 7
References
- Alaoglu, Leonidas; Erdős, Paul (1944). "On highly composite and similar numbers". Trans. Amer. Math. Soc. 56 (3): 448–469. doi:10.2307/1990319.
- Lang, Serge (1966). Introduction to transcendental numbers. Reading, Mass.: Addison-Wesley Publishing Co..
- Momot, Aleksander (2011). "Density of rational points on commutative group varieties and small transcendence degree". arXiv:1011.3368 [math.NT].
- Ramachandra, Kanakanahalli (1967–1968). "Contributions to the theory of transcendental numbers. I, II.". Acta Arith. 14: 65–72, 73–88. doi:10.4064/aa-14-1-65-72.
- Roy, Damien (1992). "Matrices whose coefficients are linear forms in logarithms". J. Number Theory 41 (1): 22–47. doi:10.1016/0022-314x(92)90081-y.
- Waldschmidt, Michel (1988). "On the transcendence methods of Gel'fond and Schneider in several variables". in Baker, Alan. New advances in transcendence theory. Cambridge University Press. pp. 375–398.
- Waldschmidt, Michel (2005). "Hopf algebras and transcendental numbers". in Aoki, Takashi; Kanemitsu, Shigeru; Nakahara, Mikio et al.. 14. Springer. pp. 197–219.
External links
- Weisstein, Eric W.. "Six exponentials theorem". http://mathworld.wolfram.com/SixExponentialsTheorem.html.
- "Six exponentials theorem". http://planetmath.org/?op=getobj&from=objects&id={{{id}}}.
 |

