Physics:Maxwell–Lodge effect

The Maxwell-Lodge effect is a phenomenon of electromagnetic induction in which an electric charge, near a solenoid in which current changes slowly, feels an electromotive force (e.m.f.) even if the magnetic field is practically static inside and null outside. It can be considered a classical analogue of the quantum mechanical Aharonov–Bohm effect, where instead the field is exactly static inside and null outside. The term appeared in the scientific literature in a 2008 article, referring to an article of 1889 by physicist Oliver Lodge.

Description

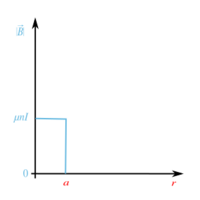
Consider an infinite solenoid (ideal solenoid) with n turns per length unit, through which a current [math]\displaystyle{ I(t) }[/math] flows. The magnetic field inside the solenoid is,

[math]\displaystyle{ \mathbf B = \mu n I(t) }[/math]      (1)

while the field outside the solenoid is null.

From the second and third Maxwell's equations,

[math]\displaystyle{ \begin{cases} \nabla \times \mathbf{E} &= -\dfrac{\partial\mathbf B}{\partial t} \\ \nabla \cdot \mathbf{B} &= 0 \end{cases} }[/math]

and from definitions of magnetic potential and electric potential stems:

[math]\displaystyle{ \mathbf E = - \mathbf \nabla \phi - \frac{\partial \mathbf A}{\partial t} }[/math]

that without electric charges reduces to

[math]\displaystyle{ \mathbf E = - \frac{\partial \mathbf A}{\partial t} }[/math]       (2)

Solenoid and B field with the flow through a surface S of base l

Resuming the original definition of Maxwell on the potential vector, according to which is a vector that its circuitation along a closed curve is equal to the flow of [math]\displaystyle{ \mathbf B }[/math] through the surface having the above curve as its edge, i.e.

[math]\displaystyle{ \int_{S} \mathbf B \cdot d \mathbf S = \int_S \nabla \times \mathbf A \cdot d \mathbf S = \oint_{l} \mathbf A \cdot d\mathbf l }[/math],

we can calculate the induced e.m.f., as Lodge did in his 1889 article, considering [math]\displaystyle{ l }[/math] the closed line around the solenoid, or convenience a circumference, and [math]\displaystyle{ S }[/math] the surface having [math]\displaystyle{ l }[/math] as border. Assuming [math]\displaystyle{ a }[/math] the radius of the solenoid and [math]\displaystyle{ r \gt a }[/math] the radius of [math]\displaystyle{ l }[/math], the surface crossing it is subjected to a magnetic flux [math]\displaystyle{ \pi a^2 \mathbf B }[/math] which is equal to circuitation [math]\displaystyle{ l }[/math]: [math]\displaystyle{ C(l) = 2\pi r \mathbf A(r) }[/math]. From that stems

[math]\displaystyle{ \mathbf A(r) = \frac{1}{2} a^2 \frac{\mathbf B}{r} }[/math].

From (2) we have that the e.m.f. is null for [math]\displaystyle{ \mathbf B }[/math] constant, which means, due to (1), at constant current.

On the other hand, if the current changes, [math]\displaystyle{ \mathbf B }[/math] must also change, producing electromagnetic waves in the surrounding space that can induce an e.m.f. outside the solenoid.

But if the current changes very slowly, one finds oneself in an almost stationary situation in which the radiative effects are negligible and therefore, excluding [math]\displaystyle{ \mathbf B }[/math], the only possible cause of the e.m.f. is [math]\displaystyle{ \mathbf A(r) }[/math].

B module as a function of the distance from the solenoid's center

A module as a function of the distance from the solenoid's center

It is possible to make calculations without referring to the field [math]\displaystyle{ \mathbf A(r) }[/math]. Indeed, in the framework of Maxwell equations as written above:

[math]\displaystyle{ \int_l \mathbf E \cdot dl =-\frac{d}{dt} \int_{S} {\mathbf B \cdot dS}= -\frac{d}{dt} \int_{\pi a^2} {\mathbf B \cdot dS} }[/math],

being [math]\displaystyle{ \mathbf B }[/math] negligible outside the solenoid. Thus

[math]\displaystyle{ \mathbf E 2\pi r= - \pi a^2 \frac{d \mathbf B}{dt} \quad \Rightarrow \quad \mathbf E= - \frac{a^2}{2r} \frac{d \mathbf B}{dt} }[/math].

This doesn't avoid the problem that [math]\displaystyle{ \mathbf B }[/math] is practically null in places where the e.m.f. manifests itself.

Interpretation

Bearing in mind that the concept of field was introduced into physics to ensure that actions on objects are always local, i.e. by contact (direct and mediated by a field) and not by remote action, as Albert Einstein feared in the EPR paradox, the result of the Maxwell-Lodge effect, like the Aharonov-Bohm effect, seems contradictory. In fact, even though the magnetic field is zero outside the solenoid and the electromagnetic radiation is negligible, a test charge experiences the presence of an electric field.

The question arises as to how the information on the presence of the magnetic field from inside the solenoid reaches the electric charge. In terms of the fields [math]\displaystyle{ \mathbf B }[/math] and [math]\displaystyle{ \mathbf E }[/math] the explanation is very simple: the variation of [math]\displaystyle{ \mathbf B }[/math] inside the solenoid produces an electric field both inside and outside the solenoid, in the same way in which a charge distribution produces an electric field both inside and outside the distribution. In this sense the information from inside and outside is mediated by the electric field which must be continuous over all space due to the Maxwell equations and their boundary condition.

From the calculations it seems evident that the source can be considered either the variation of the potential vector [math]\displaystyle{ \mathbf A }[/math], if you choose to introduce it, or that of the magnetic field [math]\displaystyle{ \mathbf B }[/math], if you do not want to use the potential vector, which in the classical context has always been considered a mathematical aid, unlike the quantum case, in which Richard Feynman proclaimed its existence as a physical reality.

See also

• Principle of locality

Further reading

• G. Rousseaux, R. Kofman, O. Minazzoli (2008). "The Maxwell-Lodge effect: significance of electromagnetic potentials in the classical theory". The European Physical Journal D 49 (2): 249–256. doi:10.1140/epjd/e2008-00142-y. Bibcode: 2008EPJD...49..249R. 
• Oliver Lodge (1889). "On an Electrostatic Field produced by varying Magnetic Induction". The Philosophical Magazine 27 (1): 469–479. doi:10.1088/1478-7814/10/1/320. Bibcode: 1888PPSL...10..116L. https://archive.org/details/s5philosophicalm27lond/page/468. 
• Sara Barbieri, Michela Cavinato e Marco Giliberti (2013). "Riscoprire il potenziale vettore per ambientarlo nella scuola superiore". European Journal of Physics 34 (15). doi:10.1088/0143-0807/34/5/1209. http://www2.fisica.unimi.it/giliberti/Pls/PLS%202016-2017/PLS%202015-2016/GDF_potenziale_vettore.pdf.