Physics:Maxwell's equations
| Part of a series of articles about |
| Electromagnetism |
|---|
 |
Maxwell's equations, or Maxwell–Heaviside equations, are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, electric and magnetic circuits. The equations provide a mathematical model for electric, optical, and radio technologies, such as power generation, electric motors, wireless communication, lenses, radar, etc. They describe how electric and magnetic fields are generated by charges, currents, and changes of the fields.[note 1] The equations are named after the physicist and mathematician James Clerk Maxwell, who, in 1861 and 1862, published an early form of the equations that included the Lorentz force law. Maxwell first used the equations to propose that light is an electromagnetic phenomenon. The modern form of the equations in their most common formulation is credited to Oliver Heaviside.[1]
Maxwell's equations may be combined to demonstrate how fluctuations in electromagnetic fields (waves) propagate at a constant speed in vacuum, c (299792458 m/s).[2] Known as electromagnetic radiation, these waves occur at various wavelengths to produce a spectrum of radiation from radio waves to gamma rays.
In differential form and SI units, Maxwell's microscopic equations can be written as With the electric field, the magnetic field, the electric charge density and the current density. is the vacuum permittivity and the vacuum permeability.
The equations have two major variants. The microscopic equations have universal applicability but are unwieldy for common calculations. They relate the electric and magnetic fields to total charge and total current, including the complicated charges and currents in materials at the atomic scale. The macroscopic equations define two new auxiliary fields that describe the large-scale behaviour of matter without having to consider atomic-scale charges and quantum phenomena like spins. However, their use requires experimentally determined parameters for a phenomenological description of the electromagnetic response of materials. The term "Maxwell's equations" is often also used for equivalent alternative formulations. Versions of Maxwell's equations based on the electric and magnetic scalar potentials are preferred for explicitly solving the equations as a boundary value problem, analytical mechanics, or for use in quantum mechanics. The covariant formulation (on spacetime rather than space and time separately) makes the compatibility of Maxwell's equations with special relativity manifest. Maxwell's equations in curved spacetime, commonly used in high-energy and gravitational physics, are compatible with general relativity.[note 2] In fact, Albert Einstein developed special and general relativity to accommodate the invariant speed of light, a consequence of Maxwell's equations, with the principle that only relative movement has physical consequences.
The publication of the equations marked the unification of a theory for previously separately described phenomena: magnetism, electricity, light, and associated radiation. Since the mid-20th century, it has been understood that Maxwell's equations do not give an exact description of electromagnetic phenomena, but are instead a classical limit of the more precise theory of quantum electrodynamics.
History of the equations
Conceptual descriptions
Gauss's law

Gauss's law describes the relationship between an electric field and electric charges: an electric field points away from positive charges and towards negative charges, and the net outflow of the electric field through a closed surface is proportional to the enclosed charge, including bound charge due to polarization of material. The coefficient of the proportion is the permittivity of free space.
Gauss's law for magnetism
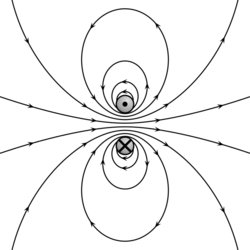
Gauss's law for magnetism states that electric charges have no magnetic analogues, called magnetic monopoles; no north or south magnetic poles exist in isolation.[3] Instead, the magnetic field of a material is attributed to a dipole, and the net outflow of the magnetic field through a closed surface is zero. Magnetic dipoles may be represented as loops of current or inseparable pairs of equal and opposite "magnetic charges". Precisely, the total magnetic flux through a Gaussian surface is zero, and the magnetic field is a solenoidal vector field.[note 3]
Faraday's law

The Maxwell–Faraday version of Faraday's law of induction describes how a time-varying magnetic field corresponds to curl of an electric field.[3] In integral form, it states that the work per unit charge required to move a charge around a closed loop equals the rate of change of the magnetic flux through the enclosed surface.
The electromagnetic induction is the operating principle behind many electric generators: for example, a rotating bar magnet creates a changing magnetic field and generates an electric field in a nearby wire.
Ampère's law with Maxwell's addition

The original law of Ampère states that magnetic fields relate to electric current. Maxwell's addition states that magnetic fields also relate to changing electric fields, which Maxwell called displacement current. The integral form states that electric and displacement currents are associated with a proportional magnetic field along any enclosing curve.
Maxwell's addition to Ampère's law is important because the laws of Ampère and Gauss must otherwise be adjusted for static fields.[4][clarification needed] As a consequence, it predicts that a rotating magnetic field occurs with a changing electric field.[3][5] A further consequence is the existence of self-sustaining electromagnetic waves which travel through empty space.
The speed calculated for electromagnetic waves, which could be predicted from experiments on charges and currents,[note 4] matches the speed of light; indeed, light is one form of electromagnetic radiation (as are X-rays, radio waves, and others). Maxwell understood the connection between electromagnetic waves and light in 1861, thereby unifying the theories of electromagnetism and optics.
Formulation in terms of electric and magnetic fields (microscopic or in vacuum version)
In the electric and magnetic field formulation there are four equations that determine the fields for given charge and current distribution. A separate law of nature, the Lorentz force law, describes how, conversely, the electric and magnetic fields act on charged particles and currents. A version of this law was included in the original equations by Maxwell but, by convention, is included no longer. The vector calculus formalism below, the work of Oliver Heaviside,[6][7] has become standard. It is manifestly rotation invariant, and therefore mathematically much more transparent than Maxwell's original 20 equations in x,y,z components. The relativistic formulations are even more symmetric and manifestly Lorentz invariant. For the same equations expressed using tensor calculus or differential forms, see § Alternative formulations.
The differential and integral formulations are mathematically equivalent; both are useful. The integral formulation relates fields within a region of space to fields on the boundary and can often be used to simplify and directly calculate fields from symmetric distributions of charges and currents. On the other hand, the differential equations are purely local and are a more natural starting point for calculating the fields in more complicated (less symmetric) situations, for example using finite element analysis.[8]
Key to the notation
Symbols in bold represent vector quantities, and symbols in italics represent scalar quantities, unless otherwise indicated. The equations introduce the electric field, E, a vector field, and the magnetic field, B, a pseudovector field, each generally having a time and location dependence. The sources are
- the total electric charge density (total charge per unit volume), ρ, and
- the total electric current density (total current per unit area), J.
The universal constants appearing in the equations (the first two ones explicitly only in the SI units formulation) are:
- the permittivity of free space, ε0, and
- the permeability of free space, μ0, and
- the speed of light,
Differential equations
In the differential equations,
- the nabla symbol, ∇, denotes the three-dimensional gradient operator, del,
- the ∇⋅ symbol (pronounced "del dot") denotes the divergence operator,
- the ∇× symbol (pronounced "del cross") denotes the curl operator.
Integral equations
In the integral equations,
- Ω is any volume with closed boundary surface ∂Ω, and
- Σ is any surface with closed boundary curve ∂Σ,
The equations are a little easier to interpret with time-independent surfaces and volumes. Time-independent surfaces and volumes are "fixed" and do not change over a given time interval. For example, since the surface is time-independent, we can bring the differentiation under the integral sign in Faraday's law: Maxwell's equations can be formulated with possibly time-dependent surfaces and volumes by using the differential version and using Gauss and Stokes formula appropriately.
-
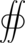 is a surface integral over the boundary surface ∂Ω, with the loop indicating the surface is closed
is a surface integral over the boundary surface ∂Ω, with the loop indicating the surface is closed - is a volume integral over the volume Ω,
- is a line integral around the boundary curve ∂Σ, with the loop indicating the curve is closed.
- is a surface integral over the surface Σ,
- The total electric charge Q enclosed in Ω is the volume integral over Ω of the charge density ρ (see the "macroscopic formulation" section below): where dV is the volume element.
- The net electric current I is the surface integral of the electric current density J passing through a fixed surface, Σ: where dS denotes the differential vector element of surface area S, normal to surface Σ. (Vector area is sometimes denoted by A rather than S, but this conflicts with the notation for magnetic vector potential).
Formulation in SI units convention
| Name | Integral equations | Differential equations |
|---|---|---|
| Gauss's law | |
|
| Gauss's law for magnetism | |
|
| Maxwell–Faraday equation (Faraday's law of induction) | ||
| Ampère's circuital law (with Maxwell's addition) |
Formulation in Gaussian units convention
The definitions of charge, electric field, and magnetic field can be altered to simplify theoretical calculation, by absorbing dimensioned factors of ε0 and μ0 into the units of calculation, by convention. With a corresponding change in convention for the Lorentz force law this yields the same physics, i.e. trajectories of charged particles, or work done by an electric motor. These definitions are often preferred in theoretical and high energy physics where it is natural to take the electric and magnetic field with the same units, to simplify the appearance of the electromagnetic tensor: the Lorentz covariant object unifying electric and magnetic field would then contain components with uniform unit and dimension.[9]: vii Such modified definitions are conventionally used with the Gaussian (CGS) units. Using these definitions and conventions, colloquially "in Gaussian units",[10] the Maxwell equations become:[11]
| Name | Integral equations | Differential equations |
|---|---|---|
| Gauss's law | |
|
| Gauss's law for magnetism | |
|
| Maxwell–Faraday equation (Faraday's law of induction) | ||
| Ampère's circuital law (with Maxwell's addition) |
The equations simplify slightly when a system of quantities is chosen in the speed of light, c, is used for nondimensionalization, so that, for example, seconds and lightseconds are interchangeable, and c = 1.
Further changes are possible by absorbing factors of 4π. This process, called rationalization, affects whether Coulomb's law or Gauss's law includes such a factor (see Heaviside–Lorentz units, used mainly in particle physics).
Relationship between differential and integral formulations
The equivalence of the differential and integral formulations are a consequence of the Gauss divergence theorem and the Kelvin–Stokes theorem.
Flux and divergence

According to the (purely mathematical) Gauss divergence theorem, the electric flux through the boundary surface ∂Ω can be rewritten as
The integral version of Gauss's equation can thus be rewritten as Since Ω is arbitrary (e.g. an arbitrary small ball with arbitrary center), this is satisfied if and only if the integrand is zero everywhere. This is the differential equations formulation of Gauss equation up to a trivial rearrangement.
Similarly rewriting the magnetic flux in Gauss's law for magnetism in integral form gives
which is satisfied for all Ω if and only if everywhere.
Circulation and curl

By the Kelvin–Stokes theorem we can rewrite the line integrals of the fields around the closed boundary curve ∂Σ to an integral of the "circulation of the fields" (i.e. their curls) over a surface it bounds, i.e.
Hence the modified Ampere law in integral form can be rewritten as Since Σ can be chosen arbitrarily, e.g. as an arbitrary small, arbitrary oriented, and arbitrary centered disk, we conclude that the integrand is zero if and only if Ampere's modified law in differential equations form is satisfied. The equivalence of Faraday's law in differential and integral form follows likewise.
The line integrals and curls are analogous to quantities in classical fluid dynamics: the circulation of a fluid is the line integral of the fluid's flow velocity field around a closed loop, and the vorticity of the fluid is the curl of the velocity field.
Charge conservation
The invariance of charge can be derived as a corollary of Maxwell's equations. The left-hand side of the modified Ampere's law has zero divergence by the div–curl identity. Expanding the divergence of the right-hand side, interchanging derivatives, and applying Gauss's law gives:
i.e., By the Gauss divergence theorem, this means the rate of change of charge in a fixed volume equals the net current flowing through the boundary:
In particular, in an isolated system the total charge is conserved.
Vacuum equations, electromagnetic waves and speed of light

In a region with no charges (ρ = 0) and no currents (J = 0), such as in a vacuum, Maxwell's equations reduce to:
Taking the curl (∇×) of the curl equations, and using the curl of the curl identity we obtain
The quantity has the dimension of (time/length)2. Defining , the equations above have the form of the standard wave equations
Already during Maxwell's lifetime, it was found that the known values for and give , then already known to be the speed of light in free space. This led him to propose that light and radio waves were propagating electromagnetic waves, since amply confirmed. In the old SI system of units, the values of and are defined constants, (which means that by definition ) that define the ampere and the metre. In the new SI system, only c keeps its defined value, and the electron charge gets a defined value.
In materials with relative permittivity, εr, and relative permeability, μr, the phase velocity of light becomes
which is usually[note 5] less than c.
In addition, E and B are perpendicular to each other and to the direction of wave propagation, and are in phase with each other. A sinusoidal plane wave is one special solution of these equations. Maxwell's equations explain how these waves can physically propagate through space. The changing magnetic field creates a changing electric field through Faraday's law. In turn, that electric field creates a changing magnetic field through Maxwell's addition to Ampère's law. This perpetual cycle allows these waves, now known as electromagnetic radiation, to move through space at velocity c.
Macroscopic formulation
The above equations are the microscopic version of Maxwell's equations, expressing the electric and the magnetic fields in terms of the (possibly atomic-level) charges and currents present. This is sometimes called the "general" form, but the macroscopic version below is equally general, the difference being one of bookkeeping.
The microscopic version is sometimes called "Maxwell's equations in a vacuum": this refers to the fact that the material medium is not built into the structure of the equations, but appears only in the charge and current terms. The microscopic version was introduced by Lorentz, who tried to use it to derive the macroscopic properties of bulk matter from its microscopic constituents.[12]: 5
"Maxwell's macroscopic equations", also known as Maxwell's equations in matter, are more similar to those that Maxwell introduced himself.
| Name | Integral equations (SI convention) |
Differential equations (SI convention) |
Differential equations (Gaussian convention) |
|---|---|---|---|
| Gauss's law | |
||
| Ampère's circuital law (with Maxwell's addition) | |||
| Gauss's law for magnetism | |
||
| Maxwell–Faraday equation (Faraday's law of induction) |
In the macroscopic equations, the influence of bound charge Qb and bound current Ib is incorporated into the displacement field D and the magnetizing field H, while the equations depend only on the free charges Qf and free currents If. This reflects a splitting of the total electric charge Q and current I (and their densities ρ and J) into free and bound parts:
The cost of this splitting is that the additional fields D and H need to be determined through phenomenological constituent equations relating these fields to the electric field E and the magnetic field B, together with the bound charge and current.
See below for a detailed description of the differences between the microscopic equations, dealing with total charge and current including material contributions, useful in air/vacuum;[note 6] and the macroscopic equations, dealing with free charge and current, practical to use within materials.
Bound charge and current

When an electric field is applied to a dielectric material its molecules respond by forming microscopic electric dipoles – their atomic nuclei move a tiny distance in the direction of the field, while their electrons move a tiny distance in the opposite direction. This produces a macroscopic bound charge in the material even though all of the charges involved are bound to individual molecules. For example, if every molecule responds the same, similar to that shown in the figure, these tiny movements of charge combine to produce a layer of positive bound charge on one side of the material and a layer of negative charge on the other side. The bound charge is most conveniently described in terms of the polarization P of the material, its dipole moment per unit volume. If P is uniform, a macroscopic separation of charge is produced only at the surfaces where P enters and leaves the material. For non-uniform P, a charge is also produced in the bulk.[13]
Somewhat similarly, in all materials the constituent atoms exhibit magnetic moments that are intrinsically linked to the angular momentum of the components of the atoms, most notably their electrons. The connection to angular momentum suggests the picture of an assembly of microscopic current loops. Outside the material, an assembly of such microscopic current loops is not different from a macroscopic current circulating around the material's surface, despite the fact that no individual charge is traveling a large distance. These bound currents can be described using the magnetization M.[14]
The very complicated and granular bound charges and bound currents, therefore, can be represented on the macroscopic scale in terms of P and M, which average these charges and currents on a sufficiently large scale so as not to see the granularity of individual atoms, but also sufficiently small that they vary with location in the material. As such, Maxwell's macroscopic equations ignore many details on a fine scale that can be unimportant to understanding matters on a gross scale by calculating fields that are averaged over some suitable volume.
Auxiliary fields, polarization and magnetization
The definitions of the auxiliary fields are:
where P is the polarization field and M is the magnetization field, which are defined in terms of microscopic bound charges and bound currents respectively. The macroscopic bound charge density ρb and bound current density Jb in terms of polarization P and magnetization M are then defined as
If we define the total, bound, and free charge and current density by and use the defining relations above to eliminate D, and H, the "macroscopic" Maxwell's equations reproduce the "microscopic" equations.
Constitutive relations
In order to apply 'Maxwell's macroscopic equations', it is necessary to specify the relations between displacement field D and the electric field E, as well as the magnetizing field H and the magnetic field B. Equivalently, we have to specify the dependence of the polarization P (hence the bound charge) and the magnetization M (hence the bound current) on the applied electric and magnetic field. The equations specifying this response are called constitutive relations. For real-world materials, the constitutive relations are rarely simple, except approximately, and usually determined by experiment. See the main article on constitutive relations for a fuller description.[15]: 44–45
For materials without polarization and magnetization, the constitutive relations are (by definition)[9]: 2 where ε0 is the permittivity of free space and μ0 the permeability of free space. Since there is no bound charge, the total and the free charge and current are equal.
An alternative viewpoint on the microscopic equations is that they are the macroscopic equations together with the statement that vacuum behaves like a perfect linear "material" without additional polarization and magnetization. More generally, for linear materials the constitutive relations are[15]: 44–45 where ε is the permittivity and μ the permeability of the material. For the displacement field D the linear approximation is usually excellent because for all but the most extreme electric fields or temperatures obtainable in the laboratory (high power pulsed lasers) the interatomic electric fields of materials of the order of 1011 V/m are much higher than the external field. For the magnetizing field , however, the linear approximation can break down in common materials like iron leading to phenomena like hysteresis. Even the linear case can have various complications, however.
- For homogeneous materials, ε and μ are constant throughout the material, while for inhomogeneous materials they depend on location within the material (and perhaps time).[16]: 463
- For isotropic materials, ε and μ are scalars, while for anisotropic materials (e.g. due to crystal structure) they are tensors.[15]: 421 [16]: 463
- Materials are generally dispersive, so ε and μ depend on the frequency of any incident EM waves.[15]: 625 [16]: 397
Even more generally, in the case of non-linear materials (see for example nonlinear optics), D and P are not necessarily proportional to E, similarly H or M is not necessarily proportional to B. In general D and H depend on both E and B, on location and time, and possibly other physical quantities.
In applications one also has to describe how the free currents and charge density behave in terms of E and B possibly coupled to other physical quantities like pressure, and the mass, number density, and velocity of charge-carrying particles. E.g., the original equations given by Maxwell (see History of Maxwell's equations) included Ohm's law in the form
Alternative formulations
Following is a summary of some of the numerous other mathematical formalisms to write the microscopic Maxwell's equations, with the columns separating the two homogeneous Maxwell equations from the two inhomogeneous ones involving charge and current. Each formulation has versions directly in terms of the electric and magnetic fields, and indirectly in terms of the electrical potential φ and the vector potential A. Potentials were introduced as a convenient way to solve the homogeneous equations, but it was thought that all observable physics was contained in the electric and magnetic fields (or relativistically, the Faraday tensor). The potentials play a central role in quantum mechanics, however, and act quantum mechanically with observable consequences even when the electric and magnetic fields vanish (Aharonov–Bohm effect).
Each table describes one formalism. See the main article for details of each formulation. SI units are used throughout.
| Formulation | Homogeneous equations | Inhomogeneous equations |
|---|---|---|
| Fields
3D Euclidean space + time |
|
|
| Potentials (any gauge)
3D Euclidean space + time |
|
|
| Potentials (Lorenz gauge)
3D Euclidean space + time |
|
|
| Formulation | Homogeneous equations | Inhomogeneous equations |
|---|---|---|
| Fields
space + time spatial metric independent of time |
||
| Potentials
space (with § topological restrictions) + time spatial metric independent of time |
|
|
| Potentials (Lorenz gauge)
space (with topological restrictions) + time spatial metric independent of time |
|
|
| Formulation | Homogeneous equations | Inhomogeneous equations |
|---|---|---|
| Fields
any space + time |
|
|
| Potentials (any gauge)
any space (with § topological restrictions) + time |
|
|
| Potential (Lorenz Gauge)
any space (with topological restrictions) + time spatial metric independent of time |
|
|
Relativistic formulations
The Maxwell equations can also be formulated on a spacetime-like Minkowski space where space and time are treated on equal footing. The direct spacetime formulations make manifest that the Maxwell equations are relativistically invariant. Because of this symmetry, the electric and magnetic fields are treated on equal footing and are recognized as components of the Faraday tensor. This reduces the four Maxwell equations to two, which simplifies the equations, although we can no longer use the familiar vector formulation. In fact the Maxwell equations in the space + time formulation are not Galileo invariant and have Lorentz invariance as a hidden symmetry. This was a major source of inspiration for the development of relativity theory. Indeed, even the formulation that treats space and time separately is not a non-relativistic approximation and describes the same physics by simply renaming variables. For this reason the relativistic invariant equations are usually called the Maxwell equations as well.
Each table below describes one formalism.
| Formulation | Homogeneous equations | Inhomogeneous equations |
|---|---|---|
| Fields Minkowski space |
||
| Potentials (any gauge) Minkowski space |
||
| Potentials (Lorenz gauge) Minkowski space |
|
|
| Fields any spacetime |
||
| Potentials (any gauge) any spacetime (with §topological restrictions) |
||
| Potentials (Lorenz gauge) any spacetime (with topological restrictions) |
|
| Formulation | Homogeneous equations | Inhomogeneous equations |
|---|---|---|
| Fields any spacetime |
||
| Potentials (any gauge) any spacetime (with topological restrictions) |
||
| Potentials (Lorenz gauge) any spacetime (with topological restrictions) |
|
- In the tensor calculus formulation, the electromagnetic tensor Fαβ is an antisymmetric covariant order 2 tensor; the four-potential, Aα, is a covariant vector; the current, Jα, is a vector; the square brackets, [ ], denote antisymmetrization of indices; ∂α is the partial derivative with respect to the coordinate, xα. In Minkowski space coordinates are chosen with respect to an inertial frame; (xα) = (ct, x, y, z), so that the metric tensor used to raise and lower indices is ηαβ = diag(1, −1, −1, −1). The d'Alembert operator on Minkowski space is ◻ = ∂α∂α as in the vector formulation. In general spacetimes, the coordinate system xα is arbitrary, the covariant derivative ∇α, the Ricci tensor, Rαβ and raising and lowering of indices are defined by the Lorentzian metric, gαβ and the d'Alembert operator is defined as ◻ = ∇α∇α. The topological restriction is that the second real cohomology group of the space vanishes (see the differential form formulation for an explanation). This is violated for Minkowski space with a line removed, which can model a (flat) spacetime with a point-like monopole on the complement of the line.
- In the differential form formulation on arbitrary space times, F = 1/2Fαβdxα ∧ dxβ is the electromagnetic tensor considered as a 2-form, A = Aαdxα is the potential 1-form, is the current 3-form, d is the exterior derivative, and is the Hodge star on forms defined (up to its orientation, i.e. its sign) by the Lorentzian metric of spacetime. In the special case of 2-forms such as F, the Hodge star depends on the metric tensor only for its local scale. This means that, as formulated, the differential form field equations are conformally invariant, but the Lorenz gauge condition breaks conformal invariance. The operator is the d'Alembert–Laplace–Beltrami operator on 1-forms on an arbitrary Lorentzian spacetime. The topological condition is again that the second real cohomology group is 'trivial' (meaning that its form follows from a definition). By the isomorphism with the second de Rham cohomology this condition means that every closed 2-form is exact.
Other formalisms include the geometric algebra formulation and a matrix representation of Maxwell's equations. Historically, a quaternionic formulation[17][18] was used.
Solutions
Maxwell's equations are partial differential equations that relate the electric and magnetic fields to each other and to the electric charges and currents. Often, the charges and currents are themselves dependent on the electric and magnetic fields via the Lorentz force equation and the constitutive relations. These all form a set of coupled partial differential equations which are often very difficult to solve: the solutions encompass all the diverse phenomena of classical electromagnetism. Some general remarks follow.
As for any differential equation, boundary conditions[19][20][21] and initial conditions[22] are necessary for a unique solution. For example, even with no charges and no currents anywhere in spacetime, there are the obvious solutions for which E and B are zero or constant, but there are also non-trivial solutions corresponding to electromagnetic waves. In some cases, Maxwell's equations are solved over the whole of space, and boundary conditions are given as asymptotic limits at infinity.[23] In other cases, Maxwell's equations are solved in a finite region of space, with appropriate conditions on the boundary of that region, for example an artificial absorbing boundary representing the rest of the universe,[24][25] or periodic boundary conditions, or walls that isolate a small region from the outside world (as with a waveguide or cavity resonator).[26]
Jefimenko's equations (or the closely related Liénard–Wiechert potentials) are the explicit solution to Maxwell's equations for the electric and magnetic fields created by any given distribution of charges and currents. It assumes specific initial conditions to obtain the so-called "retarded solution", where the only fields present are the ones created by the charges. However, Jefimenko's equations are unhelpful in situations when the charges and currents are themselves affected by the fields they create.
Numerical methods for differential equations can be used to compute approximate solutions of Maxwell's equations when exact solutions are impossible. These include the finite element method and finite-difference time-domain method.[19][21][27][28][29] For more details, see Computational electromagnetics.
Overdetermination of Maxwell's equations
Maxwell's equations seem overdetermined, in that they involve six unknowns (the three components of E and B) but eight equations (one for each of the two Gauss's laws, three vector components each for Faraday's and Ampere's laws). (The currents and charges are not unknowns, being freely specifiable subject to charge conservation.) This is related to a certain limited kind of redundancy in Maxwell's equations: It can be proven that any system satisfying Faraday's law and Ampere's law automatically also satisfies the two Gauss's laws, as long as the system's initial condition does, and assuming conservation of charge and the nonexistence of magnetic monopoles.[30][31] This explanation was first introduced by Julius Adams Stratton in 1941.[32]
Although it is possible to simply ignore the two Gauss's laws in a numerical algorithm (apart from the initial conditions), the imperfect precision of the calculations can lead to ever-increasing violations of those laws. By introducing dummy variables characterizing these violations, the four equations become not overdetermined after all. The resulting formulation can lead to more accurate algorithms that take all four laws into account.[33]
Both identities , which reduce eight equations to six independent ones, are the true reason of overdetermination.[34][35]
Equivalently, the overdetermination can be viewed as implying conservation of electric and magnetic charge, as they are required in the derivation described above but implied by the two Gauss's laws.
For linear algebraic equations, one can make 'nice' rules to rewrite the equations and unknowns. The equations can be linearly dependent. But in differential equations, and especially partial differential equations (PDEs), one needs appropriate boundary conditions, which depend in not so obvious ways on the equations. Even more, if one rewrites them in terms of vector and scalar potential, then the equations are underdetermined because of gauge fixing.
Maxwell's equations and quantum mechanics
Maxwell's equations are valid in both the classical and the Quantum realm. In the Heisenberg representation of Quantum Mechanics, the equations of the E and B operators are precisely Maxwell's equations. Of course since the fields are quantum operators, there are many aspects which differ from the classical fields. For example, the E field acts like the momentum conjugate to the spatial components of the vector potential A. This of course leads to many aspects of the quantum electromagnetic field with differ from them as classical fields but they still obey the same evolution equations as the classical field does.
Of course once one examines the effects of the electromagnetic fields on charged matter, and those effects then change the electromagnetic field are examined, the field equations become non-linear, and the quantum behaviour of non-linear field can be very different from the classical behaviour of the non-linear fields. That however does not alter the fact that if one remains in the linear regime, the fields obey Maxwell's equations.
Variations
Popular variations on the Maxwell equations as a classical theory of electromagnetic fields are relatively scarce because the standard equations have stood the test of time remarkably well.
Magnetic monopoles
Maxwell's equations posit that there is electric charge, but no magnetic charge (also called magnetic monopoles), in the universe. Indeed, magnetic charge has never been observed, despite extensive searches,[note 7] and may not exist. If they did exist, both Gauss's law for magnetism and Faraday's law would need to be modified, and the resulting four equations would be fully symmetric under the interchange of electric and magnetic fields.[9]: 273–275
See also
Explanatory notes
- ↑ Electric and magnetic fields, according to the theory of relativity, are the components of a single electromagnetic field.
- ↑ In general relativity, however, they must enter, through its stress–energy tensor, into Einstein field equations that include the spacetime curvature.
- ↑ The absence of sinks/sources of the field does not imply that the field lines must be closed or escape to infinity. They can also wrap around indefinitely, without self-intersections. Moreover, around points where the field is zero (that cannot be intersected by field lines, because their direction would not be defined), there can be the simultaneous begin of some lines and end of other lines. This happens, for instance, in the middle between two identical cylindrical magnets, whose north poles face each other. In the middle between those magnets, the field is zero and the axial field lines coming from the magnets end. At the same time, an infinite number of divergent lines emanate radially from this point. The simultaneous presence of lines which end and begin around the point preserves the divergence-free character of the field. For a detailed discussion of non-closed field lines, see L. Zilberti "The Misconception of Closed Magnetic Flux Lines", IEEE Magnetics Letters, vol. 8, art. 1306005, 2017.
- ↑ The quantity we would now call 1/√ε0μ0, with units of velocity, was directly measured before Maxwell's equations, in an 1855 experiment by Wilhelm Eduard Weber and Rudolf Kohlrausch. They charged a leyden jar (a kind of capacitor), and measured the electrostatic force associated with the potential; then, they discharged it while measuring the magnetic force from the current in the discharge wire. Their result was 3.107×108 m/s, remarkably close to the speed of light. See Joseph F. Keithley, The story of electrical and magnetic measurements: from 500 B.C. to the 1940s, p. 115.
- ↑ There are cases (anomalous dispersion) where the phase velocity can exceed c, but the "signal velocity" will still be < c
- ↑ In some books—e.g., in U. Krey and A. Owen's Basic Theoretical Physics (Springer 2007)—the term effective charge is used instead of total charge, while free charge is simply called charge.
- ↑ See magnetic monopole for a discussion of monopole searches. Recently, scientists have discovered that some types of condensed matter, including spin ice and topological insulators, which display emergent behavior resembling magnetic monopoles. (See sciencemag.org and nature.com.) Although these were described in the popular press as the long-awaited discovery of magnetic monopoles, they are only superficially related. A "true" magnetic monopole is something where ∇ ⋅ B ≠ 0, whereas in these condensed-matter systems, ∇ ⋅ B = 0 while only ∇ ⋅ H ≠ 0.
References
- ↑ Hampshire, Damian P. (29 October 2018). "A derivation of Maxwell's equations using the Heaviside notation". Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 376 (2134). doi:10.1098/rsta.2017.0447. ISSN 1364-503X. PMID 30373937. Bibcode: 2018RSPTA.37670447H.
- ↑ "The NIST Reference on Constants, Units, and Uncertainty". https://physics.nist.gov/cgi-bin/cuu/Value?c.
- ↑ 3.0 3.1 3.2 Jackson, John. "Maxwell's equations". Berkeley Lab. http://videoglossary.lbl.gov/#n45.
- ↑ J. D. Jackson, Classical Electrodynamics, section 6.3
- ↑ Principles of physics: a calculus-based text, by R. A. Serway, J. W. Jewett, page 809.
- ↑ Bruce J. Hunt (1991) The Maxwellians, chapter 5 and appendix, Cornell University Press
- ↑ "Maxwell's Equations". Engineering and Technology History Wiki. 29 October 2019. http://ethw.org/Maxwell's_Equations.
- ↑ Šolín, Pavel (2006). Partial differential equations and the finite element method. John Wiley and Sons. p. 273. ISBN 978-0-471-72070-6. https://books.google.com/books?id=-hIG3NZrnd8C&pg=PA273.
- ↑ 9.0 9.1 9.2 J. D. Jackson (1975-10-17). Classical Electrodynamics (3rd ed.). Wiley. ISBN 978-0-471-43132-9. https://archive.org/details/classicalelectro00jack_0.
- ↑ "Gaussian, SI and Other Systems of Units in Electromagnetic Theory". Physics 221A, University of California, Berkeley lecture notes. Fall 2007. http://bohr.physics.berkeley.edu/classes/221/0708/notes/emunits.pdf.
- ↑ David J Griffiths (1999). Introduction to electrodynamics (Third ed.). Prentice Hall. pp. 559–562. ISBN 978-0-13-805326-0. https://archive.org/details/introductiontoel00grif_0/page/559.
- ↑ Kimball Milton; J. Schwinger (18 June 2006). Electromagnetic Radiation: Variational Methods, Waveguides and Accelerators. Springer Science & Business Media. ISBN 978-3-540-29306-4.
- ↑ See David J. Griffiths (1999). Introduction to Electrodynamics (third ed.). Prentice Hall. ISBN 9780138053260. https://archive.org/details/introductiontoel00grif_0. for a good description of how P relates to the bound charge.
- ↑ See David J. Griffiths (1999). Introduction to Electrodynamics (third ed.). Prentice Hall. ISBN 9780138053260. https://archive.org/details/introductiontoel00grif_0. for a good description of how M relates to the bound current.
- ↑ 15.0 15.1 15.2 15.3 Andrew Zangwill (2013). Modern Electrodynamics. Cambridge University Press. ISBN 978-0-521-89697-9.
- ↑ 16.0 16.1 16.2 Kittel, Charles (2005), Introduction to Solid State Physics (8th ed.), USA: John Wiley & Sons, Inc., ISBN 978-0-471-41526-8
- ↑ Jack, P. M. (2003). "Physical Space as a Quaternion Structure I: Maxwell Equations. A Brief Note". arXiv:math-ph/0307038.
- ↑ A. Waser (2000). "On the Notation of Maxwell's Field Equations". AW-Verlag. http://www.zpenergy.com/downloads/Orig_maxwell_equations.pdf.
- ↑ 19.0 19.1 Peter Monk (2003). Finite Element Methods for Maxwell's Equations. Oxford UK: Oxford University Press. p. 1 ff. ISBN 978-0-19-850888-5. https://books.google.com/books?id=zI7Y1jT9pCwC&q=electromagnetism+%22boundary+conditions%22&pg=PA1.
- ↑ Thomas B. A. Senior & John Leonidas Volakis (1995-03-01). Approximate Boundary Conditions in Electromagnetics. London UK: Institution of Electrical Engineers. p. 261 ff. ISBN 978-0-85296-849-9. https://books.google.com/books?id=eOofBpuyuOkC&q=electromagnetism+%22boundary+conditions%22&pg=PA261.
- ↑ 21.0 21.1 T Hagstrom (Björn Engquist & Gregory A. Kriegsmann, Eds.) (1997). Computational Wave Propagation. Berlin: Springer. p. 1 ff. ISBN 978-0-387-94874-4. https://books.google.com/books?id=EdZefkIOR5cC&q=electromagnetism+%22boundary+conditions%22&pg=PA1.
- ↑ Henning F. Harmuth & Malek G. M. Hussain (1994). Propagation of Electromagnetic Signals. Singapore: World Scientific. p. 17. ISBN 978-981-02-1689-4. https://books.google.com/books?id=6_CZBHzfhpMC&q=electromagnetism+%22initial+conditions%22&pg=PA45.
- ↑ David M Cook (2002). The Theory of the Electromagnetic Field. Mineola NY: Courier Dover Publications. p. 335 ff. ISBN 978-0-486-42567-2. https://books.google.com/books?id=bI-ZmZWeyhkC&q=electromagnetism+infinity+boundary+conditions&pg=RA1-PA335.
- ↑ Jean-Michel Lourtioz (2005-05-23). Photonic Crystals: Towards Nanoscale Photonic Devices. Berlin: Springer. p. 84. ISBN 978-3-540-24431-8. https://books.google.com/books?id=vSszZ2WuG_IC&q=electromagnetism+boundary++-element&pg=PA84.
- ↑ S. G. Johnson, Notes on Perfectly Matched Layers, online MIT course notes (Aug. 2007).
- ↑ S. F. Mahmoud (1991). Electromagnetic Waveguides: Theory and Applications. London UK: Institution of Electrical Engineers. p. Chapter 2. ISBN 978-0-86341-232-5. https://books.google.com/books?id=toehQ7vLwAMC&q=Maxwell%27s+equations+waveguides&pg=PA2.
- ↑ John Leonidas Volakis, Arindam Chatterjee & Leo C. Kempel (1998). Finite element method for electromagnetics : antennas, microwave circuits, and scattering applications. New York: Wiley IEEE. p. 79 ff. ISBN 978-0-7803-3425-0. https://books.google.com/books?id=55q7HqnMZCsC&q=electromagnetism+%22boundary+conditions%22&pg=PA79.
- ↑ Bernard Friedman (1990). Principles and Techniques of Applied Mathematics. Mineola NY: Dover Publications. ISBN 978-0-486-66444-6.
- ↑ Taflove A & Hagness S C (2005). Computational Electrodynamics: The Finite-difference Time-domain Method. Boston MA: Artech House. p. Chapters 6 & 7. ISBN 978-1-58053-832-9.
- ↑ H Freistühler & G Warnecke (2001). Hyperbolic Problems: Theory, Numerics, Applications. Springer. p. 605. ISBN 9783764367107. https://books.google.com/books?id=XXX_mG0vneMC&pg=PA605.
- ↑ J Rosen (1980). "Redundancy and superfluity for electromagnetic fields and potentials". American Journal of Physics 48 (12): 1071. doi:10.1119/1.12289. Bibcode: 1980AmJPh..48.1071R.
- ↑ J. A. Stratton (1941). Electromagnetic Theory. McGraw-Hill Book Company. pp. 1–6. ISBN 9780470131534. https://books.google.com/books?id=zFeWdS2luE4C.
- ↑ B Jiang & J Wu & L. A. Povinelli (1996). "The Origin of Spurious Solutions in Computational Electromagnetics". Journal of Computational Physics 125 (1): 104. doi:10.1006/jcph.1996.0082. Bibcode: 1996JCoPh.125..104J.
- ↑ Weinberg, Steven (1972). Gravitation and Cosmology. John Wiley. pp. 161–162. ISBN 978-0-471-92567-5. https://archive.org/details/gravitationcosmo00stev_0/page/161.
- ↑ Courant, R.; Hilbert, D. (1962), Methods of Mathematical Physics: Partial Differential Equations, II, New York: Wiley-Interscience, pp. 15–18, ISBN 9783527617241, https://books.google.com/books?id=fcZV4ohrerwC
Further reading
- Imaeda, K. (1995), "Biquaternionic Formulation of Maxwell's Equations and their Solutions", in Ablamowicz, Rafał, Clifford Algebras and Spinor Structures, Springer, pp. 265–280, doi:10.1007/978-94-015-8422-7_16, ISBN 978-90-481-4525-6
Historical publications
- On Faraday's Lines of Force – 1855/56. Maxwell's first paper (Part 1 & 2) – Compiled by Blaze Labs Research (PDF).
- On Physical Lines of Force – 1861. Maxwell's 1861 paper describing magnetic lines of force – Predecessor to 1873 Treatise.
- James Clerk Maxwell, "A Dynamical Theory of the Electromagnetic Field", Philosophical Transactions of the Royal Society of London 155, 459–512 (1865). (This article accompanied a December 8, 1864 presentation by Maxwell to the Royal Society.)
- A Dynamical Theory Of The Electromagnetic Field – 1865. Maxwell's 1865 paper describing his 20 equations, link from Google Books.
- J. Clerk Maxwell (1873), "A Treatise on Electricity and Magnetism":
- The developments before relativity:
- Larmor Joseph (1897). "On a dynamical theory of the electric and luminiferous medium. Part 3, Relations with material media". Phil. Trans. R. Soc. 190: 205–300.
- Lorentz Hendrik (1899). "Simplified theory of electrical and optical phenomena in moving systems". Proc. Acad. Science Amsterdam I: 427–443.
- Lorentz Hendrik (1904). "Electromagnetic phenomena in a system moving with any velocity less than that of light". Proc. Acad. Science Amsterdam IV: 669–678.
- Henri Poincaré (1900) "La théorie de Lorentz et le Principe de Réaction" (in French), Archives Néerlandaises, V, 253–278.
- Henri Poincaré (1902) "La Science et l'Hypothèse" (in French).
- Henri Poincaré (1905) "Sur la dynamique de l'électron" (in French), Comptes Rendus de l'Académie des Sciences, 140, 1504–1508.
- Catt, Walton and Davidson. "The History of Displacement Current" . Wireless World, March 1979.
External links
- Hazewinkel, Michiel, ed. (2001), "Maxwell equations", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=p/m063140
- maxwells-equations.com — An intuitive tutorial of Maxwell's equations.
- The Feynman Lectures on Physics Vol. II Ch. 18: The Maxwell Equations
- Wikiversity Page on Maxwell's Equations
Modern treatments
- Electromagnetism (ch. 11), B. Crowell, Fullerton College
- Lecture series: Relativity and electromagnetism, R. Fitzpatrick, University of Texas at Austin
- Electromagnetic waves from Maxwell's equations on Project PHYSNET.
- MIT Video Lecture Series (36 × 50 minute lectures) (in .mp4 format) – Electricity and Magnetism Taught by Professor Walter Lewin.
Other
- Silagadze, Z. K. (2002). "Feynman's derivation of Maxwell equations and extra dimensions". Annales de la Fondation Louis de Broglie 27: 241–256. Bibcode: 2001hep.ph....6235S.
- Nature Milestones: Photons – Milestone 2 (1861) Maxwell's equations
 |

