Physics:Orders Of Coherence

Coherence is defined as the ability of waves to interfere. Intuitively, coherent waves have a well-defined constant phase relationship. However, an exclusive and extensive physical definition of coherence is more nuanced. Coherence functions, as introduced by Roy Glauber and others in the 1960s, capture the mathematics behind the intuition by defining correlation between the electric field components as coherence. These correlations between electric field components can be measured to arbitrary orders, hence leading to the concept of different orders of coherence. The coherence encountered in most optical experiments, including the classic Young's double slit experiment and Mach-Zehnder interferometer, is first order coherence. Robert Hanbury Brown and Richard Q. Twiss performed a correlation experiment in 1956, and brought to light a different kind of correlation between fields, namely the correlation of intensities, which correspond to second order coherence. Higher order coherences become relevant in photon-coincidence counting experiments. Orders of coherence can be measured using classical correlation functions or by using the quantum analogue of those functions, which take quantum mechanical description of electric field (operators) as input. While the quantum coherence functions might yield the same results as the classical functions, the underlying mechanism and description of the physical processes are fundamentally different because quantum interference deals with interference of possible histories while classical interference deals with interference of physical waves.

Definition

The electric field [math]\displaystyle{ E(\mathbf{r},t) }[/math] can be separated into its positive and negative frequency components [math]\displaystyle{ E(\mathbf{r},t) = E^+(\mathbf{r},t) + E^-(\mathbf{r},t) }[/math]. Either of the two frequency components, contains all the physical information about the wave. The classical first-order, second order and n-th order correlation function are defined as follows

[math]\displaystyle{ G_c^{(1)}(x_1, x_2) = \langle E^-(x_1) E^+(x_2) \rangle }[/math],

[math]\displaystyle{ G_c^{(2)}(x_1, x_2, x_3, x_4) = \langle E^-(x_1) E^-(x_2) E^+(x_3) E^+(x_4) \rangle }[/math],

[math]\displaystyle{ G_c^{(n)}(x_1,x_2,...,x_{2n}) = \langle E^-(x_1) ... E^-(x_n)E^+(x_{n+1}) ... E^+(x_{2n}) \rangle }[/math],

where [math]\displaystyle{ x_i }[/math] represents [math]\displaystyle{ (\mathbf{r}_i, t_i) }[/math]. While the order of the [math]\displaystyle{ E^+(\mathbf{r},t) }[/math] and [math]\displaystyle{ E^-(\mathbf{r},t) }[/math], does not matter in the classical case, as they are merely numbers and hence commute, the ordering is vital in the quantum analogue of these correlation functions. The first order correlation function, measured at the same time and position gives us the intensity i.e. [math]\displaystyle{ G_c^{(1)}(x_1, x_1) = I }[/math]. The classical n-th order normalized correlation function is defined by dividing the n-th order correlation function by all corresponding intensities: [math]\displaystyle{ \gamma^{(n)}(x_1,...,x_n;x_n,...,x_1) = \frac{G_c^{(n)}(x_1,...,x_n;x_n,...,x_1)}{G_c^{(1)}(x_1,x_1)...G^{(1)}(x_n,x_n)} }[/math].

In quantum mechanics, the positive and negative frequency components of the electric field are replaced by the operators [math]\displaystyle{ \hat{E}^+ }[/math] and [math]\displaystyle{ \hat{E}^- }[/math] respectively. In the Heisenberg picture, [math]\displaystyle{ \hat{E}^+ = i \sum\limits_{\mathbf{k},\mu} \sqrt{\frac{\hbar \omega_k}{2 \epsilon_0 V}} \hat{a}_{\mathbf{k},\mu} e^{i \mathbf{k}.\mathbf{r}} \mathbf{e}_{\mathbf{k},\mu} }[/math], where [math]\displaystyle{ \mathbf{k} }[/math] is the polarization vector, [math]\displaystyle{ \mathbf{e}_{\mathbf{k},\mu} }[/math] is the unit vector perpendicular to [math]\displaystyle{ \mathbf{k} }[/math], with [math]\displaystyle{ \mu }[/math] signifying one of the two vectors that are perpedincular to the polarization vector, [math]\displaystyle{ \omega_k }[/math] is the frequency of the mode and [math]\displaystyle{ V }[/math] is the volume. The n-th order quantum correlation function is defined as:

[math]\displaystyle{ G^{(n)}(x_1,...,x_{2n}) = Tr[\hat{\rho} \hat{E}^{-}(x_1) ... \hat{E}^{-}(x_n) \hat{E}^{+}(x_{n+1}) ... \hat{E}^{+}(x_{2n})] }[/math].

Here the orders of the [math]\displaystyle{ \hat{E}^+ }[/math] and [math]\displaystyle{ \hat{E}^- }[/math] operators do matter. This is because the positive and the negative frequency ([math]\displaystyle{ \hat{E}^+ }[/math] and [math]\displaystyle{ \hat{E}^- }[/math]) components are proportional the annhiliation and the creation operators respectively, and [math]\displaystyle{ \hat{a} }[/math] and [math]\displaystyle{ \hat{a}^{\dagger} }[/math] do not commute. When the operators are written in the order shown in the equation above, they are said to be in a normal ordering. Subsequently, the n-th order normalized correlation function is defined as:

[math]\displaystyle{ g^{(n)}(x_1,...,x_n;x_n,...,x_1) = \frac{G^{(n)}(x_1,...,x_n;x_n,...,x_1)}{G^{(1)}(x_1,x_1)...G^{(1)}(x_n,x_n)} }[/math].

A field is said to m-coherent if the m-th normalized correlation function is unity. This definition holds for both [math]\displaystyle{ \gamma^{(m)} }[/math] and [math]\displaystyle{ g^{(m)} }[/math].

Young Double Slit Experiment

Figure 1. Schematic diagram for the setup of the Young's Double Slit Experiment.

In Young's double slit experiment, light from a light source is allowed to pass through two pinholes separated by some distance, and a screen is placed some distance away from the pinholes where the interference between the light waves is observed (Figure. 1). Young's double slit experiment demonstrates the dependence of interference on coherence, specifically on the first-order correlation. This experiment is equivalent to the Mach-Zehnder interferometer with the caveat that Young's double slit experiment is concerned with spatial coherence, while Mach-Zehnder interferometer relies on temporal coherence.

The intensity measured at the position [math]\displaystyle{ \mathbf{r} }[/math] at time [math]\displaystyle{ t }[/math] is

[math]\displaystyle{ \langle I \rangle = \langle |E^+(\mathbf{r},t)|^2 \rangle = \langle I \rangle =I_1 + I_2 + 2 \sqrt{I_1 I_2} |\gamma^{(1)}(x_1,x_2)| cos \phi(x_1,x_2) }[/math].

Light field has highest degree of coherence when the corresponding interference pattern has the maximum contrast on the screen. The fringe contrast is defined as [math]\displaystyle{ V = \frac{I_{max} - I_{min}}{I_{max} + I_{min}} }[/math].

Classically, [math]\displaystyle{ I^{max}_{min} = I_1 + I_2 \pm 2 \sqrt{I_1 I_2} |\gamma^{(1)}(x_1,x_2)| }[/math] and hence [math]\displaystyle{ V = \frac{2 \sqrt{I_1 I_2}|\gamma^{(1)}(x_1,x_2)|}{I_1 + I_2} }[/math]. As coherence is the ability to interfere visibility and coherence are linked:

[math]\displaystyle{ |\gamma^{(1)}(x_1,x_2)| = 1 }[/math] means highest contrast, complete coherence

[math]\displaystyle{ 0 \lt |\gamma^{(1)}(x_1,x_2)| \lt 1 }[/math] means partial fringe visibility, partial coherence

[math]\displaystyle{ |\gamma^{(1)}(x_1,x_2)| = 0 }[/math] means no contrast, complete incoherence.

Quantum Description

Classically, the electric field at a position [math]\displaystyle{ \mathbf{r} }[/math], is the sum of electric field components from at the two pinholes [math]\displaystyle{ \mathbf{r}_1 }[/math] and [math]\displaystyle{ \mathbf{r}_2 }[/math] earlier times [math]\displaystyle{ t_1, t_2 }[/math] respectably i.e. [math]\displaystyle{ E^+(\mathbf{r},t) = E^+(\mathbf{r_1},t_1) + E^+(\mathbf{r}_2,t_2) }[/math]. Correspondingly, in the quantum description the electric field operators are similarly related, [math]\displaystyle{ \hat{E}^+(\mathbf{r},t) = \hat{E}^+(\mathbf{r_1},t_1) + \hat{E}^+(\mathbf{r}_2,t_2) }[/math]. This implies

[math]\displaystyle{ I = Tr[\rho \hat{E}^-(\mathbf{r},t) \hat{E}^+(\mathbf{r},t)] = I_1 + I_2 + 2 \sqrt{I_1 I_2} |g^{(1)}(x_1,x_2)| cos \phi(x_1,x_2) }[/math].

The intensity fluctuates as a function of position i.e. the quantum mechanical treatment also predicts interference fringes. Moreover, in accordance to the intuitive understanding of coherence i.e. ability to interfere, the interference patterns depend on the first-order correlation function [math]\displaystyle{ g^{(1)} }[/math]. Comparing this to the classical intensity, we note that the only difference is that the classical normalized correlation [math]\displaystyle{ \gamma^{(1)} }[/math] is now replaced by the quantum correlation [math]\displaystyle{ g^{(1)} }[/math]. Even the computations here look strikingly similar to the ones that might be done classically. However, the quantum interference that occurs in this process is fundamentally different from the classical interference of electromagnetic waves. Quantum interference occurs when two possible histories, given a particular initial and final state, interfere. In this experiment, given an initial state of the photon before the pinhole and it final state at the screen, the two possible histories correspond to the two pinholes through which the photon could have passed. Hence, quantum mechanically, here the photon is interfering with itself. Such interference of different histories, however, occurs only when the observer has no specific way of determining which of the different histories actually occurred. If the system is observed to determine the path of the photon, then on average the interference of amplitudes will vanish.

Hanbury Brown and Twiss Experiment

Figure 2. A schematic diagram for the setup for Hanbury Brown and Twiss's original experiment.

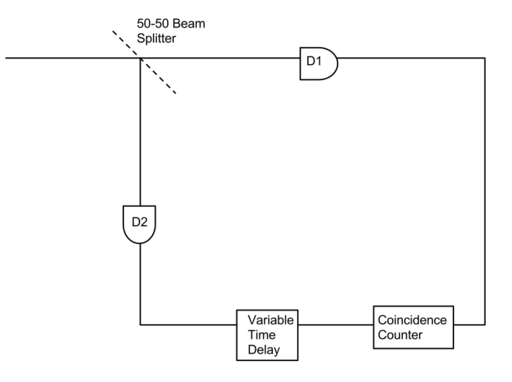
In the Hanbury Brown and Twiss experiment (Figure 2.), a light beam is split using a beam splitter and then detected by detectors, which are equidistant from the beam splitter. Subsequently, signal measured by the second detector is delayed by time [math]\displaystyle{ \tau }[/math] and the coincidence rate between the original and delayed signal is counted. This experiment correlates intensities, [math]\displaystyle{ |E^+(\mathbf{r},t + \tau)E^+(\mathbf{r},t)|^2 }[/math], rather than electric fields and hence measures the second order correlation function

[math]\displaystyle{ G_c^{(2)}(t,t+\tau, t + \tau, t) = \langle E^-(t) E^-(t + \tau) E^+(t + \tau) E^+(t)\rangle }[/math].

Under the assumption of stationary statistics, at a given position, the normalized correlation function is

[math]\displaystyle{ g^{(2)}= \frac{\langle \hat{E}^-(0) \hat{E}^-(\tau) \hat{E}^+(\tau) \hat{E}^+(0) \rangle}{ \langle \hat{E}^-(0) \hat{E}^+(0) \rangle \langle \hat{E}^-(\tau) \hat{E}^+(\tau) \rangle} }[/math]

[math]\displaystyle{ g^{(2)} }[/math] here measures the probability of coincidence of two photons being detected with a time difference [math]\displaystyle{ \tau }[/math].

For all varieties of chaotic light, the following relationship between the first order and second-order coherences holds:

[math]\displaystyle{ g^{(2)}(\tau) = 1 + |g^{(1)}(\tau)|^2 }[/math].

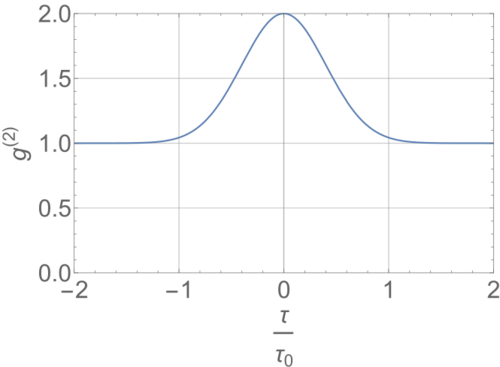
This relationship is true for both the classical and quantum correlation functions. Moreover, as [math]\displaystyle{ |g^{(1)}(\tau)| }[/math] always takes a value between 0 and 1, for a chaotic light beam, [math]\displaystyle{ 1\leq g^{(2)}\leq 2 }[/math]. The light source used by Hanbury Brown and Twiss was stellar light which is chaotic. Hanbury Brown and Twiss used this result to compute the first order coherence from their measurement of the second order coherence. The observed second order coherence the curve was as shown in figure 2.

For Gaussian light source [math]\displaystyle{ g^{(1)} = e^{-i \omega_0 \tau -\frac{\pi}{2}(\frac{\tau}{\tau_0})^2} }[/math]. Often a Gaussian light source is chaotic and consequently,

Figure 3. The second order coherence for stellar light as measured in the Hanbury Brown and Twiss experiment as a function of the time delay introduced between the signals [math]\displaystyle{ \tau / \tau_0 }[/math], where [math]\displaystyle{ \tau_0 }[/math] is the coherence length.

[math]\displaystyle{ g^{(2)}(\tau) = 1 + e^{-\frac{\pi}{2}(\frac{\tau}{\tau_0})^2} }[/math].

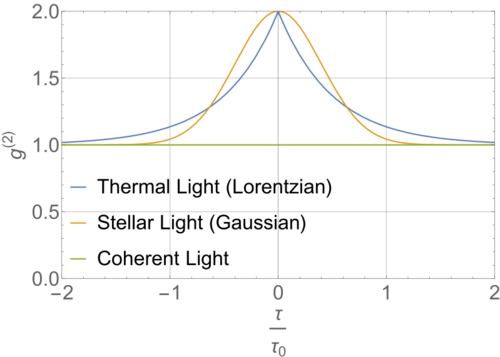
This model fits the observation that was done by Hanbury Brown and Twiss using stellar light as demonstrated in figure 3. If thermal light was used instead of stellar light in the same setup, then we would see a different function for the second order coherence. Thermal light can be modeled to be a Lorentzian power spectrum centered around frequency [math]\displaystyle{ \omega_0 }[/math], which means [math]\displaystyle{ \langle E^*(0) E(\tau) \rangle = E_0^2 e^{-|\tau|/\tau_0} }[/math], where [math]\displaystyle{ \tau_0 }[/math] is the coherence length of the beam. Correspondingly, [math]\displaystyle{ g^{(1)} = e^{-i \omega_0 \tau -|\tau|/\tau_0} }[/math] and [math]\displaystyle{ g^{(2)}(\tau) = 1 + e^{-2 |\tau|/ \tau_0} }[/math]. The second-order coherence for stellar (Gaussian), thermal (Lorentzian) and coherent light is shown in Figure 4. Note that when stellar/thermal light beam is first order coherent i.e. [math]\displaystyle{ g^{(1)}(0)=1 }[/math], the second order coherence is 2, meaning at zero time delay chaotic light right is first order coherent but not second order coherent.

Quantum Description

Classically, we can think of a light beam as having a probability distribution as a function of mode amplitudes, [math]\displaystyle{ P(\{ \alpha_k \}) }[/math] and in that case, the second order correlation function [math]\displaystyle{ G^{(2)}(\tau,0) = \langle E^-(\tau)E^+(\tau)E^-(0)E^+(0)\rangle \int P(\{ \alpha_k \}) E^*(\tau)E(\tau)E^*(0)E(0) d\{ \alpha_k \} }[/math]. If we assume that the quantum state of the setup is [math]\displaystyle{ \rho = \int d\{ \alpha_k \} P(\{ \alpha_k \}) |\{ \alpha_k \} \rangle \langle \{ \alpha_k \}| }[/math], then the quantum mechanical correlation function,[math]\displaystyle{ G^{(2)}(\tau,0) = Tr[ \rho \hat{E}^-(\tau)\hat{E}^+(\tau)\hat{E}^-(0)\hat{E}^+(0)]= \int P(\{ \alpha_k \}) E^*(\tau)E(\tau)E^*(0)E(0) d\{ \alpha_k \} }[/math], which is same as the classical result.

Figure 4. The second order coherence for thermal, stellar and coherent light as a function of time delay. [math]\displaystyle{ \tau_0 }[/math] is the coherence length of the light beam.

Similar to the case of Young's double slit experiment, the classical and the quantum description lead to the same result, but that does not mean that two descriptions are equivalent. Classically, the light beams arrives as an electromagnetic wave and interferes owing to the superposition principle. The quantum description is not as straightforward. To understand the subtleties in the quantum description, assume that photons from the source are emitted independent of each other at the source and that the photons are not split by the beam splitter. When the intensity of the source is set to be very low, such that only one photon might be detected at any time, accounting for the fact that there might be accidental coincidences, which are statistically independent of time, the coincidence counter should not change with respect to the time difference. However, as shown in Figure 3., for stellar light [math]\displaystyle{ g^{(2)}(\tau) = 1 + e^{-2 |\tau|/ \tau_0} }[/math], so without any time delay [math]\displaystyle{ g^{(2)}(0) = 2 }[/math] and with a large time delay [math]\displaystyle{ \lim_{\tau \rightarrow \infty}g^{(2)}(\tau) = 1 }[/math]. Hence, even when there was no time-delay the photons from the source were arriving in pairs! This effect is termed photon bunching. Moreover, if a laser light was used at the source instead of chaotic light, then second order coherence would be independent of the time delay. HBT's experiment allows for a fundamentally distinction in the way in which photons are emitted from a laser compared to a natural light source. Such a distinction is not captured by the classical description on wave interference.

Higher Order Coherences and Mathematical Properties of Coherence Functions

For the purposes of standard optical experiments, coherence is just first-order coherence and higher-order coherences are generally ignored. Higher order coherences are measured in photon-coincidence counting experiments. Correlation interferometry uses coherences of fourth-order and higher to perform stellar measurements. We can think of [math]\displaystyle{ G^{(n)}(x_1,...,x_n;x_n,...,x_1) }[/math] as the average coincidence rate of detecting [math]\displaystyle{ n }[/math] photons at [math]\displaystyle{ x_1,...,x_n }[/math] positions. Physically, these rate are always positive and therefore [math]\displaystyle{ G^{(n)}(x_1,...,x_n;x_n,...,x_1) \geq 0 }[/math].

m-th order coherent fields

A field is called m-th order coherent if there exists a function [math]\displaystyle{ E(x) }[/math] such that all correlation functions for [math]\displaystyle{ n \lt m }[/math] factorize. Notationally, this means

[math]\displaystyle{ G^{(n)}(x_1,...,x_{2n}) = \prod\limits_{j=1}^{n} E^*(j)E^*(j+1) }[/math]

This factorizability of all [math]\displaystyle{ n\lt m }[/math] correlation functions implies that [math]\displaystyle{ |G^{(n)}(x_1,...,x_{2n})|^2 = \prod\limits_{j=1}^{2n} G^{(1)}(x_j,x_j) }[/math]. As [math]\displaystyle{ g^{(n)}(x_1,...,x_{2n}) }[/math] was defined to be [math]\displaystyle{ \frac{G^{(n)}(x_1,...,x_n;x_n,...,x_1)}{\prod\limits_{j=1}^{n} G^{(1)}(x_j,x_j)} }[/math], it follows that [math]\displaystyle{ |g^{(n)}(x_1,...,x_{2n})|=1 }[/math] for [math]\displaystyle{ n\lt m }[/math], if the field is m-coherent. For a m-coherent field, the [math]\displaystyle{ m }[/math] photons being detected will be detected statistically independent of each other.

Upper bound the order of coherence

Given an upper bound on how many photons can be present in the field, there is an upper bound on the M-th coherence the field can have. This is because [math]\displaystyle{ \hat{E}^+ }[/math] is proportional the annihilation operator. To see this, begin with a mixed state for the field [math]\displaystyle{ \sum\limits_{n,m} c_{n,m} | n \rangle \langle m | }[/math]. If this sum has an upper limit on n,m i.e. [math]\displaystyle{ M \gt n,m }[/math], [math]\displaystyle{ Tr[\rho \hat{E}^+(x_1)...\hat{E}^+(x_p)] }[/math] is proportional to [math]\displaystyle{ Tr[\sum\limits_{n,m} c_{n,m} \hat{a}...(\text{p times})...\hat{a} |n \rangle \langle m| ] = \sum\limits_{n,m} c_{n,m} \langle m|\hat{a}...(\text{p times})...\hat{a} |n \rangle =0 }[/math] for [math]\displaystyle{ p \gt m }[/math]. This result would be unintuitive in a classical description, but fortunately such a case has no classical counterpart because we cannot put an upper bound on the number of photons in the classical case.

Stationarity of the statistics

When dealing with classical optics, physicists often employ the assumption that the statistics of the system are stationary. This means that while the observations might fluctuate, the underlying statistics of the system remains constant as time progresses. The quantum analogue of stationary statistics is to require that the density operator, which contains the information about the wavefunction, commutes with the Hamiltonian. Owing to Schrödinger equation, [math]\displaystyle{ \frac{d \rho}{dt} = \frac{-i}{h}[H,\rho] }[/math], stationary statistics implies that the density operator is independent of time. Consequently, in[math]\displaystyle{ G^{(n)}(x_1,...,x_{2n}) }[/math], owing to the cyclicity of the trace, we can transform the time independence of the density operator in the Schrödinger picture to the time independence of [math]\displaystyle{ \hat{E}^{+} }[/math] and [math]\displaystyle{ \hat{E}^{-} }[/math], in the Heisenberg picture, giving us

[math]\displaystyle{ G^{(n)}(x_1,...,x_{2n}) = Tr[\hat{\rho} \hat{E}^{-}(x_1,t) .... \hat{E}^{-}(x_n,t) \hat{E}^{+}(x_{n+1},t) ...\hat{E}^{+}(x_{2n,t})] }[/math] [math]\displaystyle{ = Tr[\hat{\rho} \hat{E}^{-}(x_1,t+\tau) .... \hat{E}^{-}(x_n,t+\tau) \hat{E}^{+}(x_{n+1},t+\tau) ... \hat{E}^{+}(x_{2n},t+\tau)] }[/math].

This means that under the assumption that the underlying statistics of the system are stationary, the n-th order correlation functions do not change when every time argument is translated by the same amount. In other words, rather than looking at actual times, the correlation function is only concerned with the [math]\displaystyle{ 2n-1 }[/math] time differences.

Coherent States

Coherent state are quantum mechanical states that have the maximal coherence and have the most "classical"-like behavior. A coherent state is defined as the quantum mechanical state that is the eigenstate of the electric field operator [math]\displaystyle{ \hat{E}^+ }[/math]. As [math]\displaystyle{ \hat{E}^+ }[/math] is directly proportional to the annihilation operator the coherent state is an eigenstate of the annihilation operator. Given a coherent state [math]\displaystyle{ | \alpha \rangle }[/math], [math]\displaystyle{ G^{(n)}(x_1,...,x_{2n}) = Tr[\sum\limits_{n,m} c_{n,m} \hat{a}...\hat{a} | \alpha \rangle \langle \alpha| ] = \langle \alpha|\hat{a}...(\text{p times})...\hat{a} |\alpha \rangle = 1 }[/math]. Consequently, coherent states have all orders of coherences as being non-zero.

See also

• Degree of coherence
• Hanbury Brown and Twiss effect
• Double-slit experiment
• Young's interference experiment
• Mach–Zehnder interferometer