Physics:Mach–Zehnder interferometer

| Part of a series on |
| Quantum mechanics |
|---|
The Mach–Zehnder interferometer is a device used to determine the relative phase shift variations between two collimated beams derived by splitting light from a single source. The interferometer has been used, among other things, to measure phase shifts between the two beams caused by a sample or a change in length of one of the paths. The apparatus is named after the physicists Ludwig Mach (the son of Ernst Mach) and Ludwig Zehnder; Zehnder's proposal in an 1891 article[1] was refined by Mach in an 1892 article.[2] Mach–Zehnder interferometry has been demonstrated with electrons as well as with light.[3] The versatility of the Mach–Zehnder configuration has led to its being used in a range of research topics efforts especially in fundamental quantum mechanics.
Design
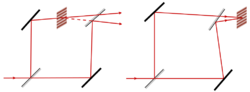
The Mach–Zehnder interferometer is a highly configurable instrument. In contrast to the well-known Michelson interferometer, each of the well-separated light paths is traversed only once.
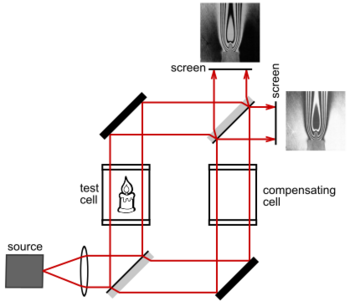
If the source has a low coherence length then great care must be taken to equalize the two optical paths. White light in particular requires the optical paths to be simultaneously equalized over all wavelengths, or no fringes will be visible (unless a monochromatic filter is used to isolate a single wavelength). As seen in Fig. 1, a compensating cell made of the same type of glass as the test cell (so as to have equal optical dispersion) would be placed in the path of the reference beam to match the test cell. Note also the precise orientation of the beam splitters. The reflecting surfaces of the beam splitters would be oriented so that the test and reference beams pass through an equal amount of glass. In this orientation, the test and reference beams each experience two front-surface reflections, resulting in the same number of phase inversions. The result is that light travels through an equal optical path length in both the test and reference beams leading to constructive interference.[4][5]
Collimated sources result in a nonlocalized fringe pattern. Localized fringes result when an extended source is used. In Fig. 2, we see that the fringes can be adjusted so that they are localized in any desired plane.[6]: 18 In most cases, the fringes would be adjusted to lie in the same plane as the test object, so that fringes and test object can be photographed together.
Operation

The collimated beam is split by a half-silvered mirror. The two resulting beams (the "sample beam" and the "reference beam") are each reflected by a mirror. The two beams then pass a second half-silvered mirror and enter two detectors.
The Fresnel equations for reflection and transmission of a wave at a dielectric imply that there is a phase change for a reflection, when a wave propagating in a lower-refractive index medium reflects from a higher-refractive index medium, but not in the opposite case. A 180° phase shift occurs upon reflection from the front of a mirror, since the medium behind the mirror (glass) has a higher refractive index than the medium the light is traveling in (air). No phase shift accompanies a rear-surface reflection, since the medium behind the mirror (air) has a lower refractive index than the medium the light is traveling in (glass).
The speed of light is lower in media with an index of refraction greater than that of a vacuum, which is 1. Specifically, its speed is: v = c/n, where c is the speed of light in vacuum, and n is the index of refraction. This causes a phase shift increase proportional to (n − 1) × length traveled. If k is the constant phase shift incurred by passing through a glass plate on which a mirror resides, a total of 2k phase shift occurs when reflecting from the rear of a mirror. This is because light traveling toward the rear of a mirror will enter the glass plate, incurring k phase shift, and then reflect from the mirror with no additional phase shift, since only air is now behind the mirror, and travel again back through the glass plate, incurring an additional k phase shift.
The rule about phase shifts applies to beamsplitters constructed with a dielectric coating and must be modified if a metallic coating is used or when different polarizations are taken into account. Also, in real interferometers, the thicknesses of the beamsplitters may differ, and the path lengths are not necessarily equal. Regardless, in the absence of absorption, conservation of energy guarantees that the two paths must differ by a half-wavelength phase shift. Also beamsplitters that are not 50/50 are frequently employed to improve the interferometer's performance in certain types of measurement.[4]
In Fig. 3, in the absence of a sample, both the sample beam (SB) and the reference beam (RB) will arrive in phase at detector 1, yielding constructive interference. Both SB and RB will have undergone a phase shift of (1 × wavelength + k) due to two front-surface reflections and one transmission through a glass plate. At detector 2, in the absence of a sample, the sample beam and reference beam will arrive with a phase difference of half a wavelength, yielding complete destructive interference. The RB arriving at detector 2 will have undergone a phase shift of (0.5 × wavelength + 2k) due to one front-surface reflection and two transmissions. The SB arriving at detector 2 will have undergone a (1 × wavelength + 2k) phase shift due to two front-surface reflections, one rear-surface reflection. Therefore, when there is no sample, only detector 1 receives light. If a sample is placed in the path of the sample beam, the intensities of the beams entering the two detectors will change, allowing the calculation of the phase shift caused by the sample.
Quantum treatment
We can model a photon going through the interferometer by assigning a probability amplitude to each of the two possible paths: the "lower" path which starts from the left, goes straight through both beam splitters, and ends at the top, and the "upper" path which starts from the bottom, goes straight through both beam splitters, and ends at the right. The quantum state describing the photon is therefore a vector that is a superposition of the "lower" path and the "upper" path , that is, for complex such that .
Both beam splitters are modelled as the unitary matrix , which means that when a photon meets the beam splitter it will either stay on the same path with a probability amplitude of , or be reflected to the other path with a probability amplitude of . The phase shifter on the upper arm is modelled as the unitary matrix , which means that if the photon is on the "upper" path it will gain a relative phase of , and it will stay unchanged if it is on the lower path.
A photon that enters the interferometer from the left will then end up described by the state
and the probabilities that it will be detected at the right or at the top are given respectively by
One can therefore use the Mach–Zehnder interferometer to estimate the phase shift by estimating these probabilities.
It is interesting to consider what would happen if the photon were definitely in either the "lower" or "upper" paths between the beam splitters. This can be accomplished by blocking one of the paths, or equivalently by removing the first beam splitter (and feeding the photon from the left or the bottom, as desired). In both cases there will no longer be interference between the paths, and the probabilities are given by , independently of the phase . From this we can conclude that the photon does not take one path or another after the first beam splitter, but rather that it must be described by a genuine quantum superposition of the two paths.[7]
Uses
The Mach–Zehnder interferometer's relatively large and freely accessible working space, and its flexibility in locating the fringes has made it the interferometer of choice for visualizing flow in wind tunnels[8][9] and for flow visualization studies in general. It is frequently used in the fields of aerodynamics, plasma physics and heat transfer to measure pressure, density, and temperature changes in gases.[6]: 18, 93–95
Mach–Zehnder interferometers are used in electro-optic modulators, electronic devices used in various fiber-optic communication applications. Mach–Zehnder modulators are incorporated in monolithic integrated circuits and offer well-behaved, high-bandwidth electro-optic amplitude and phase responses over a multiple-gigahertz frequency range.
Mach–Zehnder interferometers are also used to study one of the most counterintuitive predictions of quantum mechanics, the phenomenon known as quantum entanglement.[10][11]
The possibility to easily control the features of the light in the reference channel without disturbing the light in the object channel popularized the Mach–Zehnder configuration in holographic interferometry. In particular, optical heterodyne detection with an off-axis, frequency-shifted reference beam ensures good experimental conditions for shot-noise limited holography with video-rate cameras,[12] vibrometry,[13] and laser Doppler imaging of blood flow.[14]
In optical telecommunications it is used as an electro-optic modulator for phase and amplitude modulation of light. Optical computing researchers have proposed using Mach-Zehnder interferometer configurations in optical neural chips for greatly accelerating complex-valued neural network algorithms.[15]
The versatility of the Mach–Zehnder configuration has led to its being used in a wide range of fundamental research topics in quantum mechanics, including studies on counterfactual definiteness, quantum entanglement, quantum computation, quantum cryptography, quantum logic, Elitzur–Vaidman bomb tester, the quantum eraser experiment, the quantum Zeno effect, and neutron diffraction.
See also
References
- ↑ Zehnder, Ludwig (1891). "Ein neuer Interferenzrefraktor". Zeitschrift für Instrumentenkunde 11: 275–285. https://archive.org/details/zeitschriftfrin11gergoog.
- ↑ Mach, Ludwig (1892). "Ueber einen Interferenzrefraktor". Zeitschrift für Instrumentenkunde 12: 89–93. https://archive.org/details/zeitschriftfrin14gergoog.
- ↑ Ji, Yang; Chung, Yunchul; Sprinzak, D.; Heiblum, M.; Mahalu, D.; Shtrikman, Hadas (March 2003). "An electronic Mach–Zehnder interferometer" (in en). Nature 422 (6930): 415–418. doi:10.1038/nature01503. ISSN 0028-0836. PMID 12660779. Bibcode: 2003Natur.422..415J. http://www.nature.com/articles/nature01503.
- ↑ 4.0 4.1 Zetie, K. P.; Adams, S. F.; Tocknell, R. M.. "How does a Mach–Zehnder interferometer work?". Physics Department, Westminster School, London. http://www.cs.princeton.edu/courses/archive/fall06/cos576/papers/zetie_et_al_mach_zehnder00.pdf.
- ↑ Ashkenas, Harry I. (1950). The design and construction of a Mach–Zehnder interferometer for use with the GALCIT Transonic Wind Tunnel. Engineer's thesis (engd). California Institute of Technology. doi:10.7907/D0V1-MJ80.
- ↑ 6.0 6.1 Hariharan, P. (2007). Basics of Interferometry. Elsevier Inc.. ISBN 978-0-12-373589-8.
- ↑ Vedral, Vlatko (2006). Introduction to Quantum Information Science. Oxford University Press. ISBN 978-0-19-921570-6. OCLC 442351498.
- ↑ Chevalerias, R.; Latron, Y.; Veret, C. (1957). "Methods of Interferometry Applied to the Visualization of Flows in Wind Tunnels". Journal of the Optical Society of America 47 (8): 703. doi:10.1364/JOSA.47.000703. Bibcode: 1957JOSA...47..703C.
- ↑ Ristić, Slavica. "Flow visualization techniques in wind tunnels – optical methods (Part II)". Military Technical Institute, Serbia. http://www.vti.mod.gov.rs/ntp/rad2007/2-07/rist/rist.pdf.
- ↑ Paris, M. G. A. (1999). "Entanglement and visibility at the output of a Mach–Zehnder interferometer". Physical Review A 59 (2): 1615–1621. doi:10.1103/PhysRevA.59.1615. Bibcode: 1999PhRvA..59.1615P. http://qinf.fisica.unimi.it/~paris/PDF/visent.pdf. Retrieved 2 April 2012.
- ↑ Haack, G. R.; Förster, H.; Büttiker, M. (2010). "Parity detection and entanglement with a Mach-Zehnder interferometer". Physical Review B 82 (15). doi:10.1103/PhysRevB.82.155303. Bibcode: 2010PhRvB..82o5303H.
- ↑ Michel Gross; Michael Atlan (2007). "Digital holography with ultimate sensitivity". Optics Letters 32 (8): 909–911. doi:10.1364/OL.32.000909. PMID 17375150. Bibcode: 2007OptL...32..909G.
- ↑ Francois Bruno; Jérôme Laurent; Daniel Royer; Michael Atlan (2014). "Holographic imaging of surface acoustic waves". Applied Physics Letters 104 (1): 083504. doi:10.1063/1.4861116. Bibcode: 2014ApPhL.104a3504Y.
- ↑ Caroline Magnain; Amandine Castel; Tanguy Boucneau; Manuel Simonutti; Isabelle Ferezou; Armelle Rancillac; Tania Vitalis; José-Alain Sahel et al. (2014). "Holographic laser Doppler imaging of microvascular blood flow". Journal of the Optical Society of America A 31 (12): 2723–2735. doi:10.1364/JOSAA.31.002723. PMID 25606762. Bibcode: 2014JOSAA..31.2723M.
- ↑ Zhang, H.; Gu, M.; Jiang, X. D.; Thompson, J.; Cai, H.; Paesani, S.; Santagati, R.; Laing, A. et al. (January 19, 2021). "An optical neural chip for implementing complex-valued neural network". Nature Communications 12 (1): 457. doi:10.1038/s41467-020-20719-7. ISSN 2041-1723. PMID 33469031.
External links
- Mach-Zehnder - Virtual Lab by Quantum Flytrap, an interactive simulation for both classical and quantum interference, described in Migdał, Piotr; Jankiewicz, Klementyna; Grabarz, Paweł; Decaroli, Chiara; Cochin, Philippe (2022). "Visualizing quantum mechanics in an interactive simulation - Virtual Lab by Quantum Flytrap". Optical Engineering 61 (8). doi:10.1117/1.OE.61.8.081808.
 |
