Fisher's z-distribution
|
Probability density function 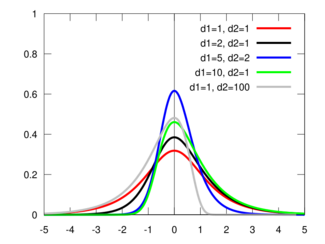 | |||
| Parameters | [math]\displaystyle{ d_1\gt 0,\ d_2\gt 0 }[/math] deg. of freedom | ||
|---|---|---|---|
| Support | [math]\displaystyle{ x \in (-\infty; +\infty)\! }[/math] | ||
| [math]\displaystyle{ \frac{2d_1^{d_1/2}d_2^{d_2/2}}{B(d_1/2,d_2/2)}\frac{e^{d_1x}}{\left(d_1e^{2x}+d_2\right)^{\left(d_1+d_2\right)/2}}\! }[/math] | |||
| Mode | [math]\displaystyle{ 0 }[/math] | ||
Fisher's z-distribution is the statistical distribution of half the logarithm of an F-distribution variate:
- [math]\displaystyle{ z = \frac 1 2 \log F }[/math]
It was first described by Ronald Fisher in a paper delivered at the International Mathematical Congress of 1924 in Toronto.[1] Nowadays one usually uses the F-distribution instead.
The probability density function and cumulative distribution function can be found by using the F-distribution at the value of [math]\displaystyle{ x' = e^{2x} \, }[/math]. However, the mean and variance do not follow the same transformation.
The probability density function is[2][3]
- [math]\displaystyle{ f(x; d_1, d_2) = \frac{2d_1^{d_1/2} d_2^{d_2/2}}{B(d_1/2, d_2/2)} \frac{e^{d_1 x}}{\left(d_1 e^{2 x} + d_2\right)^{(d_1+d_2)/2}}, }[/math]
where B is the beta function.
When the degrees of freedom becomes large ([math]\displaystyle{ d_1, d_2 \rightarrow \infty }[/math]), the distribution approaches normality with mean[2]
- [math]\displaystyle{ \bar{x} = \frac 1 2 \left( \frac 1 {d_2} - \frac 1 {d_1} \right) }[/math]
and variance
- [math]\displaystyle{ \sigma^2_x = \frac 1 2 \left( \frac 1 {d_1} + \frac 1 {d_2} \right). }[/math]
Related distribution
- If [math]\displaystyle{ X \sim \operatorname{FisherZ}(n,m) }[/math] then [math]\displaystyle{ e^{2X} \sim \operatorname{F}(n,m) \, }[/math] (F-distribution)
- If [math]\displaystyle{ X \sim \operatorname{F}(n,m) }[/math] then [math]\displaystyle{ \tfrac{\log X}{2} \sim \operatorname{FisherZ}(n,m) }[/math]
References
- ↑ Fisher, R. A. (1924). "On a Distribution Yielding the Error Functions of Several Well Known Statistics". Proceedings of the International Congress of Mathematics, Toronto 2: 805–813. http://digital.library.adelaide.edu.au/coll/special/fisher/36.pdf.
- ↑ 2.0 2.1 Leo A. Aroian (December 1941). "A study of R. A. Fisher's z distribution and the related F distribution". The Annals of Mathematical Statistics 12 (4): 429–448. doi:10.1214/aoms/1177731681.
- ↑ Charles Ernest Weatherburn (1961). A first course in mathematical statistics. https://archive.org/details/firstcourseinmat029137mbp.
External links
 |


