F-distribution

Short description: Continuous probability distribution

Fisher–Snedecor

Probability density function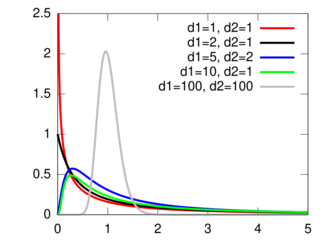
Cumulative distribution function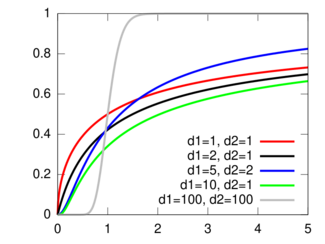
Parameters	d1, d2 > 0 deg. of freedom
Support	[math]\displaystyle{ x \in (0, +\infty)\; }[/math] if [math]\displaystyle{ d_1 = 1 }[/math], otherwise [math]\displaystyle{ x \in [0, +\infty)\; }[/math]
PDF	[math]\displaystyle{ \frac{\sqrt{\frac{(d_1 x)^{d_1} d_2^{d_2}}{(d_1 x+d_2)^{d_1+d_2}}}}{x\,\mathrm{B}\!\left(\frac{d_1}{2},\frac{d_2}{2}\right)}\! }[/math]
CDF	[math]\displaystyle{ I_{\frac{d_1 x}{d_1 x + d_2}} \left(\tfrac{d_1}{2}, \tfrac{d_2}{2} \right) }[/math]
Mean	[math]\displaystyle{ \frac{d_2}{d_2-2}\! }[/math] for d2 > 2
Mode	[math]\displaystyle{ \frac{d_1-2}{d_1}\;\frac{d_2}{d_2+2} }[/math] for d1 > 2
Variance	[math]\displaystyle{ \frac{2\,d_2^2\,(d_1+d_2-2)}{d_1 (d_2-2)^2 (d_2-4)}\! }[/math] for d2 > 4
Skewness	[math]\displaystyle{ \frac{(2 d_1 + d_2 - 2) \sqrt{8 (d_2-4)}}{(d_2-6) \sqrt{d_1 (d_1 + d_2 -2)}}\! }[/math] for d2 > 6
Kurtosis	see text
Entropy	[math]\displaystyle{ \ln \Gamma \left(\tfrac{d_1}{2} \right) + \ln \Gamma \left(\tfrac{d_2}{2} \right) - \ln \Gamma \left(\tfrac{d_1+d_2}{2} \right) + \! }[/math] [math]\displaystyle{ \left(1-\tfrac{d_1}{2} \right) \psi \left(1+\tfrac{d_1}{2} \right) - \left(1+\tfrac{d_2}{2} \right) \psi \left(1+\tfrac{d_2}{2} \right) \! }[/math] [math]\displaystyle{ + \left(\tfrac{d_1 + d_2}{2} \right) \psi \left(\tfrac{d_1 + d_2}{2} \right) + \ln \frac{d_1}{d_2} \! }[/math]
MGF	does not exist, raw moments defined in text and in
CF	see text

In probability theory and statistics, the F-distribution or F-ratio, also known as Snedecor's F distribution or the Fisher–Snedecor distribution (after Ronald Fisher and George W. Snedecor), is a continuous probability distribution that arises frequently as the null distribution of a test statistic, most notably in the analysis of variance (ANOVA) and other F-tests.

Definition

The F-distribution with d₁ and d₂ degrees of freedom is the distribution of

[math]\displaystyle{ X = \frac{S_1/d_1}{S_2/d_2} }[/math]

where [math]\displaystyle{ S_1 }[/math] and [math]\displaystyle{ S_2 }[/math] are independent random variables with chi-square distributions with respective degrees of freedom [math]\displaystyle{ d_1 }[/math] and [math]\displaystyle{ d_2 }[/math].

It can be shown to follow that the probability density function (pdf) for X is given by

[math]\displaystyle{ \begin{align} f(x; d_1,d_2) &= \frac{\sqrt{\frac{(d_1x)^{d_1}\,\,d_2^{d_2}} {(d_1x+d_2)^{d_1+d_2}}}} {x\operatorname{B}\left(\frac{d_1}{2},\frac{d_2}{2}\right)} \\[5pt] &=\frac{1}{\operatorname{B}\left(\frac{d_1}{2},\frac{d_2}{2}\right)} \left(\frac{d_1}{d_2}\right)^{\frac{d_1}{2}} x^{\frac{d_1}{2} - 1} \left(1+\frac{d_1}{d_2} \, x \right)^{-\frac{d_1+d_2}{2}} \end{align} }[/math]

for real x > 0. Here [math]\displaystyle{ \mathrm{B} }[/math] is the beta function. In many applications, the parameters d₁ and d₂ are positive integers, but the distribution is well-defined for positive real values of these parameters.

The cumulative distribution function is

[math]\displaystyle{ F(x; d_1,d_2)=I_{d_1 x/(d_1 x + d_2)}\left (\tfrac{d_1}{2}, \tfrac{d_2}{2} \right) , }[/math]

where I is the regularized incomplete beta function.

The expectation, variance, and other details about the F(d₁, d₂) are given in the sidebox; for d₂ > 8, the excess kurtosis is

[math]\displaystyle{ \gamma_2 = 12\frac{d_1(5d_2-22)(d_1+d_2-2)+(d_2-4)(d_2-2)^2}{d_1(d_2-6)(d_2-8)(d_1+d_2-2)}. }[/math]

The k-th moment of an F(d₁, d₂) distribution exists and is finite only when 2k < d₂ and it is equal to

[math]\displaystyle{ \mu _X(k) =\left( \frac{d_2}{d_1}\right)^k \frac{\Gamma \left(\tfrac{d_1}{2}+k\right) }{\Gamma \left(\tfrac{d_1}{2}\right)} \frac{\Gamma \left(\tfrac{d_2}{2}-k\right) }{\Gamma \left( \tfrac{d_2}{2}\right) }. }[/math]

The F-distribution is a particular parametrization of the beta prime distribution, which is also called the beta distribution of the second kind.

The characteristic function is listed incorrectly in many standard references (e.g.,). The correct expression is

[math]\displaystyle{ \varphi^F_{d_1, d_2}(s) = \frac{\Gamma\left(\frac{d_1+d_2}{2}\right)}{\Gamma\left(\tfrac{d_2}{2}\right)} U \! \left(\frac{d_1}{2},1-\frac{d_2}{2},-\frac{d_2}{d_1} \imath s \right) }[/math]

where U(a, b, z) is the confluent hypergeometric function of the second kind.

Characterization

A random variate of the F-distribution with parameters [math]\displaystyle{ d_1 }[/math] and [math]\displaystyle{ d_2 }[/math] arises as the ratio of two appropriately scaled chi-squared variates:

[math]\displaystyle{ X = \frac{U_1/d_1}{U_2/d_2} }[/math]

where

• [math]\displaystyle{ U_1 }[/math] and [math]\displaystyle{ U_2 }[/math] have chi-squared distributions with [math]\displaystyle{ d_1 }[/math] and [math]\displaystyle{ d_2 }[/math] degrees of freedom respectively, and
• [math]\displaystyle{ U_1 }[/math] and [math]\displaystyle{ U_2 }[/math] are independent.

In instances where the F-distribution is used, for example in the analysis of variance, independence of [math]\displaystyle{ U_1 }[/math] and [math]\displaystyle{ U_2 }[/math] might be demonstrated by applying Cochran's theorem.

Equivalently, the random variable of the F-distribution may also be written

[math]\displaystyle{ X = \frac{s_1^2}{\sigma_1^2} \div \frac{s_2^2}{\sigma_2^2}, }[/math]

where [math]\displaystyle{ s_1^2 = \frac{S_1^2}{d_1} }[/math] and [math]\displaystyle{ s_2^2 = \frac{S_2^2}{d_2} }[/math], [math]\displaystyle{ S_1^2 }[/math] is the sum of squares of [math]\displaystyle{ d_1 }[/math] random variables from normal distribution [math]\displaystyle{ N(0,\sigma_1^2) }[/math] and [math]\displaystyle{ S_2^2 }[/math] is the sum of squares of [math]\displaystyle{ d_2 }[/math] random variables from normal distribution [math]\displaystyle{ N(0,\sigma_2^2) }[/math].

In a frequentist context, a scaled F-distribution therefore gives the probability [math]\displaystyle{ p(s_1^2/s_2^2 \mid \sigma_1^2, \sigma_2^2) }[/math], with the F-distribution itself, without any scaling, applying where [math]\displaystyle{ \sigma_1^2 }[/math] is being taken equal to [math]\displaystyle{ \sigma_2^2 }[/math]. This is the context in which the F-distribution most generally appears in F-tests: where the null hypothesis is that two independent normal variances are equal, and the observed sums of some appropriately selected squares are then examined to see whether their ratio is significantly incompatible with this null hypothesis.

The quantity [math]\displaystyle{ X }[/math] has the same distribution in Bayesian statistics, if an uninformative rescaling-invariant Jeffreys prior is taken for the prior probabilities of [math]\displaystyle{ \sigma_1^2 }[/math] and [math]\displaystyle{ \sigma_2^2 }[/math]. In this context, a scaled F-distribution thus gives the posterior probability [math]\displaystyle{ p(\sigma^2_2 /\sigma_1^2 \mid s^2_1, s^2_2) }[/math], where the observed sums [math]\displaystyle{ s^2_1 }[/math] and [math]\displaystyle{ s^2_2 }[/math] are now taken as known.

Properties and related distributions

• If [math]\displaystyle{ X \sim \chi^2_{d_1} }[/math] and [math]\displaystyle{ Y \sim \chi^2_{d_2} }[/math] (Chi squared distribution) are independent, then [math]\displaystyle{ \frac{X / d_1}{Y / d_2} \sim \mathrm{F}(d_1, d_2) }[/math]
• If [math]\displaystyle{ X_k \sim \Gamma(\alpha_k,\beta_k)\, }[/math] (Gamma distribution) are independent, then [math]\displaystyle{ \frac{\alpha_2\beta_1 X_1}{\alpha_1\beta_2 X_2} \sim \mathrm{F}(2\alpha_1, 2\alpha_2) }[/math]
• If [math]\displaystyle{ X \sim \operatorname{Beta}(d_1/2,d_2/2) }[/math] (Beta distribution) then [math]\displaystyle{ \frac{d_2 X}{d_1(1-X)} \sim \operatorname{F}(d_1,d_2) }[/math]
• Equivalently, if [math]\displaystyle{ X \sim F(d_1, d_2) }[/math], then [math]\displaystyle{ \frac{d_1 X/d_2}{1+d_1 X/d_2} \sim \operatorname{Beta}(d_1/2,d_2/2) }[/math].
• If [math]\displaystyle{ X \sim F(d_1, d_2) }[/math], then [math]\displaystyle{ \frac{d_1}{d_2}X }[/math] has a beta prime distribution: [math]\displaystyle{ \frac{d_1}{d_2}X \sim \operatorname{\beta^\prime}\left(\tfrac{d_1}{2},\tfrac{d_2}{2}\right) }[/math].
• If [math]\displaystyle{ X \sim F(d_1, d_2) }[/math] then [math]\displaystyle{ Y = \lim_{d_2 \to \infty} d_1 X }[/math] has the chi-squared distribution [math]\displaystyle{ \chi^2_{d_1} }[/math]
• [math]\displaystyle{ F(d_1, d_2) }[/math] is equivalent to the scaled Hotelling's T-squared distribution [math]\displaystyle{ \frac{d_2}{d_1(d_1+d_2-1)} \operatorname{T}^2 (d_1, d_1 +d_2-1) }[/math].
• If [math]\displaystyle{ X \sim F(d_1, d_2) }[/math] then [math]\displaystyle{ X^{-1} \sim F(d_2, d_1) }[/math].
• If [math]\displaystyle{ X\sim t_{(n)} }[/math] — Student's t-distribution — then: [math]\displaystyle{ \begin{align} X^{2} &\sim \operatorname{F}(1, n) \\ X^{-2} &\sim \operatorname{F}(n, 1) \end{align} }[/math]
• F-distribution is a special case of type 6 Pearson distribution
• If [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] are independent, with [math]\displaystyle{ X,Y\sim }[/math] Laplace(μ, b) then [math]\displaystyle{ \frac{|X-\mu|}{|Y-\mu|} \sim \operatorname{F}(2,2) }[/math]
• If [math]\displaystyle{ X\sim F(n,m) }[/math] then [math]\displaystyle{ \tfrac{\log{X}}{2} \sim \operatorname{FisherZ}(n,m) }[/math] (Fisher's z-distribution)
• The noncentral F-distribution simplifies to the F-distribution if [math]\displaystyle{ \lambda=0 }[/math].
• The doubly noncentral F-distribution simplifies to the F-distribution if [math]\displaystyle{ \lambda_1 = \lambda_2 = 0 }[/math]
• If [math]\displaystyle{ \operatorname{Q}_X(p) }[/math] is the quantile p for [math]\displaystyle{ X\sim F(d_1,d_2) }[/math] and [math]\displaystyle{ \operatorname{Q}_Y(1-p) }[/math] is the quantile [math]\displaystyle{ 1-p }[/math] for [math]\displaystyle{ Y\sim F(d_2,d_1) }[/math], then [math]\displaystyle{ \operatorname{Q}_X(p)=\frac{1}{\operatorname{Q}_Y(1-p)}. }[/math]
• F-distribution is an instance of ratio distributions
• W-distribution is a unique parametrization of F-distribution.

See also

• Beta prime distribution
• Chi-square distribution
• Chow test
• Gamma distribution
• Hotelling's T-squared distribution
• Wilks' lambda distribution
• Wishart distribution
• Modified half-normal distribution with the pdf on [math]\displaystyle{ (0, \infty) }[/math] is given as [math]\displaystyle{ f(x)= \frac{2\beta^{\frac{\alpha}{2}} x^{\alpha-1} \exp(-\beta x^2+ \gamma x )}{\Psi{\left(\frac{\alpha}{2}, \frac{ \gamma}{\sqrt{\beta}}\right)}} }[/math], where [math]\displaystyle{ \Psi(\alpha,z)={}_1\Psi_1\left(\begin{matrix}\left(\alpha,\frac{1}{2}\right)\\(1,0)\end{matrix};z \right) }[/math] denotes the Fox–Wright Psi function.

External links

• Table of critical values of the F-distribution
• Earliest Uses of Some of the Words of Mathematics: entry on F-distribution contains a brief history
• Free calculator for F-testing