Icosahedral bipyramid
From HandWiki
| Icosahedral bipyramid | ||
|---|---|---|
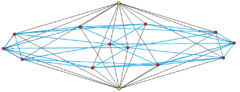 Orthogonal projection Central icosahedron with 30 blue edges and 20 red vertices, apex vertices in yellow, connecting to icosahedron with 24 black edges. | ||
| Type | Polyhedral bipyramid | |
| Schläfli symbol | {3,5} + { } dt{2,5,3} | |
| Coxeter-Dynkin | ||
| Cells | 40 {3,3} | |
| Faces | 80 {3} | |
| Edges | 54 (30+12+12) | |
| Vertices | 14 (12+2) | |
| Dual | Dodecahedral prism | |
| Symmetry group | [2,3,5], order 240 | |
| Properties | convex, regular-celled, Blind polytope | |
In 4-dimensional geometry, the icosahedral bipyramid is the direct sum of a icosahedron and a segment, {3,5} + { }. Each face of a central icosahedron is attached with two tetrahedra, creating 40 tetrahedral cells, 80 triangular faces, 54 edges, and 14 vertices.[1] An icosahedral bipyramid can be seen as two icosahedral pyramids augmented together at their bases.
It is the dual of a dodecahedral prism, Coxeter-Dynkin diagram ![]()
![]()
![]()
![]()
![]()
![]()
![]() , so the bipyramid can be described as
, so the bipyramid can be described as ![]()
![]()
![]()
![]()
![]()
![]()
![]() . Both have Coxeter notation symmetry [2,3,5], order 240.
. Both have Coxeter notation symmetry [2,3,5], order 240.
Having all regular cells (tetrahedra), it is a Blind polytope.
See also
- Pentagonal bipyramid - A lower dimensional analogy
- Tetrahedral bipyramid
- Octahedral bipyramid - A lower symmetry form of the as 16-cell.
- Cubic bipyramid
- Dodecahedral bipyramid
References
- Klitzing, Richard, "Johnson solids, Blind polytopes, and CRFs", Polytopes, https://bendwavy.org/klitzing/explain/johnson.htm, retrieved 2022-11-14
External links
 |

