16-cell
- REDIRECT Template:Infobox 4-polytope
This page is a redirect. The following categories are used to track and monitor this redirect:
|
In geometry, the 16-cell is the regular convex 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {3,3,4}. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century.[1] It is also called C16, hexadecachoron,[2] or hexdecahedroid [sic?] .[3]
It is the 4-dimesional member of an infinite family of polytopes called cross-polytopes, orthoplexes, or hyperoctahedrons which are analogous to the octahedron in three dimensions. It is Coxeter's [math]\displaystyle{ \beta_4 }[/math] polytope.[4] The dual polytope is the tesseract (4-cube), which it can be combined with to form a compound figure. The cells of the 16-cell are dual to the 16 vertices of the tesseract.
Geometry
The 16-cell is the second in the sequence of 6 convex regular 4-polytopes (in order of size and complexity).[lower-alpha 1]
Each of its 4 successor convex regular 4-polytopes can be constructed as the convex hull of a polytope compound of multiple 16-cells: the 16-vertex tesseract as a compound of two 16-cells, the 24-vertex 24-cell as a compound of three 16-cells, the 120-vertex 600-cell as a compound of fifteen 16-cells, and the 600-vertex 120-cell as a compound of seventy-five 16-cells.[lower-alpha 2]
Coordinates
| Disjoint squares | ||||||
|---|---|---|---|---|---|---|
| ||||||
| ||||||
The 16-cell is the 4-dimensional cross polytope, which means its vertices lie in opposite pairs on the 4 axes of a (w, x, y, z) Cartesian coordinate system.
The eight vertices are (±1, 0, 0, 0), (0, ±1, 0, 0), (0, 0, ±1, 0), (0, 0, 0, ±1). All vertices are connected by edges except opposite pairs. The edge length is √2.
The vertex coordinates form 6 orthogonal central squares lying in the 6 coordinate planes. Squares in opposite planes that do not share an axis (e.g. in the xy and wz planes) are completely disjoint (they do not intersect at any vertices).[lower-alpha 3]
The 16-cell constitutes an orthonormal basis for the choice of a 4-dimensional reference frame, because its vertices exactly define the four orthogonal axes.
Structure
The Schläfli symbol of the 16-cell is {3,3,4}, indicating that its cells are regular tetrahedra {3,3} and its vertex figure is a regular octahedron {3,4}. There are 8 tetrahedra, 12 triangles, and 6 edges meeting at every vertex. Its edge figure is a square. There are 4 tetrahedra and 4 triangles meeting at every edge.
The 16-cell is bounded by 16 cells, all of which are regular tetrahedra.[lower-alpha 5] It has 32 triangular faces, 24 edges, and 8 vertices. The 24 edges bound 6 orthogonal central squares lying on great circles in the 6 coordinate planes (3 pairs of completely orthogonal[lower-alpha 6] great squares). At each vertex, 3 great squares cross perpendicularly. The 6 edges meet at the vertex the way 6 edges meet at the apex of a canonical octahedral pyramid.[lower-alpha 4] The 6 orthogonal central planes of the 16-cell can be divided into 4 orthogonal central hyperplanes (3-spaces) each forming an octahedron with 3 orthogonal great squares.
Rotations
 A 3D projection of a 16-cell performing a simple rotation |
 A 3D projection of a 16-cell performing a double rotation |
Rotations in 4-dimensional Euclidean space can be seen as the composition of two 2-dimensional rotations in completely orthogonal planes.[6] The 16-cell is a simple frame in which to observe 4-dimensional rotations, because each of the 16-cell's 6 great squares has another completely orthogonal great square (there are 3 pairs of completely orthogonal squares).[lower-alpha 3] Many rotations of the 16-cell can be characterized by the angle of rotation in one of its great square planes (e.g. the xy plane) and another angle of rotation in the completely orthogonal great square plane (the wz plane).[lower-alpha 10] Completely orthogonal great squares have disjoint vertices: 4 of the 16-cell's 8 vertices rotate in one plane, and the other 4 rotate independently in the completely orthogonal plane.[lower-alpha 7]
In 2 or 3 dimensions a rotation is characterized by a single plane of rotation; this kind of rotation taking place in 4-space is called a simple rotation, in which only one of the two completely orthogonal planes rotates (the angle of rotation in the other plane is 0). In the 16-cell, a simple rotation in one of the 6 orthogonal planes moves only 4 of the 8 vertices; the other 4 remain fixed. (In the simple rotation animation above, all 8 vertices move because the plane of rotation is not one of the 6 orthogonal basis planes.)
In a double rotation both sets of 4 vertices move, but independently: the angles of rotation may be different in the 2 completely orthogonal planes. If the two angles happen to be the same, a maximally symmetric isoclinic rotation takes place.[lower-alpha 17] In the 16-cell an isoclinic rotation by 90 degrees of any pair of completely orthogonal square planes takes every square plane to its completely orthogonal square plane.[lower-alpha 18]
Constructions
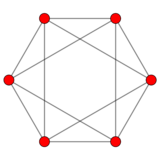
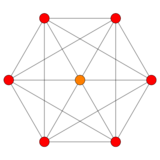
Octahedral dipyramid
| Octahedron [math]\displaystyle{ \beta_3 }[/math] | 16-cell [math]\displaystyle{ \beta_4 }[/math] |
|---|---|
|
|
| Orthogonal projections to skew hexagon hyperplane | |
The simplest construction of the 16-cell is on the 3-dimensional cross polytope, the octahedron. The octahedron has 3 perpendicular axes and 6 vertices in 3 opposite pairs (its Petrie polygon is the hexagon). Add another pair of vertices, on a fourth axis perpendicular to all 3 of the other axes. Connect each new vertex to all 6 of the original vertices, adding 12 new edges. This raises two octahedral pyramids on a shared octahedron base that lies in the 16-cell's central hyperplane.[10]

The octahedron that the construction starts with has three perpendicular intersecting squares (which appear as rectangles in the hexagonal projections). Each square intersects with each of the other squares at two opposite vertices, with two of the squares crossing at each vertex. Then two more points are added in the fourth dimension (above and below the 3-dimensional hyperplane). These new vertices are connected to all the octahedron's vertices, creating 12 new edges and three more squares (which appear edge-on as the 3 diameters of the hexagon in the projection), and three more octahedra.[lower-alpha 8]
Something unprecedented has also been created. Notice that each square no longer intersects with all of the other squares: it does intersect with four of them (with three of the squares crossing at each vertex now), but each square has one other square with which it shares no vertices: it is not directly connected to that square at all. These two separate perpendicular squares (there are three pairs of them) are like the opposite edges of a tetrahedron: perpendicular, but non-intersecting. They lie opposite each other (parallel in some sense), and they don't touch, but they also pass through each other like two perpendicular links in a chain (but unlike links in a chain they have a common center). They are an example of Clifford parallel planes, and the 16-cell is the simplest regular polytope in which they occur. Clifford parallelism[lower-alpha 12] of objects of more than one dimension (more than just curved lines) emerges here and occurs in all the subsequent 4-dimensional regular polytopes, where it can be seen as the defining relationship among disjoint concentric regular 4-polytopes and their corresponding parts. It can occur between congruent (similar) polytopes of 2 or more dimensions.[11] For example, as noted above all the subsequent convex regular 4-polytopes are compounds of multiple 16-cells; those 16-cells are Clifford parallel polytopes.
Tetrahedral constructions
|
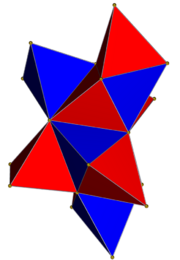
|
The 16-cell has two Wythoff constructions from regular tetrahedra, a regular form and alternated form, shown here as nets, the second represented by tetrahedral cells of two alternating colors. The alternated form is a lower symmetry construction of the 16-cell called the demitesseract.
Wythoff's construction replicates the 16-cell's characteristic 5-cell in a kaleidoscope of mirrors. Every regular 4-polytope has its characteristic 4-orthoscheme, an irregular 5-cell.[lower-alpha 19] There are three regular 4-polytopes with tetrahedral cells: the 5-cell, the 16-cell, and the 600-cell. Although all are bounded by regular tetrahedron cells, their characteristic 5-cells (4-orthoschemes) are different tetrahedral pyramids, all based on the same characteristic irregular tetrahedron. They share the same characteristic tetrahedron (3-orthoscheme) and characteristic right triangle (2-orthoscheme) because they have the same kind of cell.[lower-alpha 20]
| Characteristics of the 16-cell[13] | |||||
|---|---|---|---|---|---|
| edge[14] | arc | dihedral[15] | |||
| 𝒍 | [math]\displaystyle{ \sqrt{2} \approx 1.414 }[/math] | 90° | [math]\displaystyle{ \tfrac{\pi}{2} }[/math] | 120° | [math]\displaystyle{ \tfrac{2\pi}{3} }[/math] |
| 𝟀 | [math]\displaystyle{ \sqrt{\tfrac{2}{3}} \approx 0.816 }[/math] | 60″ | [math]\displaystyle{ \tfrac{\pi}{3} }[/math] | 60° | [math]\displaystyle{ \tfrac{\pi}{3} }[/math] |
| 𝝉[lower-alpha 21] | [math]\displaystyle{ \sqrt{\tfrac{1}{2}} \approx 0.707 }[/math] | 45″ | [math]\displaystyle{ \tfrac{\pi}{4} }[/math] | 45° | [math]\displaystyle{ \tfrac{\pi}{4} }[/math] |
| 𝟁 | [math]\displaystyle{ \sqrt{\tfrac{1}{6}} \approx 0.408 }[/math] | 30″ | [math]\displaystyle{ \tfrac{\pi}{6} }[/math] | 60° | [math]\displaystyle{ \tfrac{\pi}{3} }[/math] |
| [math]\displaystyle{ _0R^3/l }[/math] | [math]\displaystyle{ \sqrt{\tfrac{3}{4}} \approx 0.866 }[/math] | 60° | [math]\displaystyle{ \tfrac{\pi}{3} }[/math] | 90° | [math]\displaystyle{ \tfrac{\pi}{2} }[/math] |
| [math]\displaystyle{ _1R^3/l }[/math] | [math]\displaystyle{ \sqrt{\tfrac{1}{4}} = 0.5 }[/math] | 45° | [math]\displaystyle{ \tfrac{\pi}{4} }[/math] | 90° | [math]\displaystyle{ \tfrac{\pi}{2} }[/math] |
| [math]\displaystyle{ _2R^3/l }[/math] | [math]\displaystyle{ \sqrt{\tfrac{1}{12}} \approx 0.289 }[/math] | 30° | [math]\displaystyle{ \tfrac{\pi}{6} }[/math] | 90° | [math]\displaystyle{ \tfrac{\pi}{2} }[/math] |
| [math]\displaystyle{ _0R^4/l }[/math] | [math]\displaystyle{ 1 }[/math] | ||||
| [math]\displaystyle{ _1R^4/l }[/math] | [math]\displaystyle{ \sqrt{\tfrac{1}{2}} \approx 0.707 }[/math] | ||||
| [math]\displaystyle{ _2R^4/l }[/math] | [math]\displaystyle{ \sqrt{\tfrac{1}{3}} \approx 0.577 }[/math] | ||||
| [math]\displaystyle{ _3R^4/l }[/math] | [math]\displaystyle{ \sqrt{\tfrac{1}{4}} = 0.5 }[/math] | ||||
The characteristic 5-cell of the regular 16-cell is represented by the Coxeter-Dynkin diagram ![]()
![]()
![]()
![]()
![]()
![]()
![]() , which can be read as a list of the dihedral angles between its mirror facets. It is an irregular tetrahedral pyramid based on the characteristic tetrahedron of the regular tetrahedron. The regular 16-cell is subdivided by its symmetry hyperplanes into 384 instances of its characteristic 5-cell that all meet at its center.
, which can be read as a list of the dihedral angles between its mirror facets. It is an irregular tetrahedral pyramid based on the characteristic tetrahedron of the regular tetrahedron. The regular 16-cell is subdivided by its symmetry hyperplanes into 384 instances of its characteristic 5-cell that all meet at its center.
The characteristic 5-cell (4-orthoscheme) has four more edges than its base characteristic tetrahedron (3-orthoscheme), joining the four vertices of the base to its apex (the fifth vertex of the 4-orthoscheme, at the center of the regular 16-cell).[lower-alpha 22] If the regular 16-cell has unit radius edge and edge length 𝒍 = [math]\displaystyle{ \sqrt{2} }[/math], its characteristic 5-cell's ten edges have lengths [math]\displaystyle{ \sqrt{\tfrac{2}{3}} }[/math], [math]\displaystyle{ \sqrt{\tfrac{1}{2}} }[/math], [math]\displaystyle{ \sqrt{\tfrac{1}{6}} }[/math] around its exterior right-triangle face (the edges opposite the characteristic angles 𝟀, 𝝉, 𝟁),[lower-alpha 21] plus [math]\displaystyle{ \sqrt{\tfrac{3}{4}} }[/math], [math]\displaystyle{ \sqrt{\tfrac{1}{4}} }[/math], [math]\displaystyle{ \sqrt{\tfrac{1}{12}} }[/math] (the other three edges of the exterior 3-orthoscheme facet the characteristic tetrahedron, which are the characteristic radii of the regular tetrahedron), plus [math]\displaystyle{ 1 }[/math], [math]\displaystyle{ \sqrt{\tfrac{1}{2}} }[/math], [math]\displaystyle{ \sqrt{\tfrac{1}{3}} }[/math], [math]\displaystyle{ \sqrt{\tfrac{1}{4}} }[/math] (edges which are the characteristic radii of the regular 16-cell). The 4-edge path along orthogonal edges of the orthoscheme is [math]\displaystyle{ \sqrt{\tfrac{1}{2}} }[/math], [math]\displaystyle{ \sqrt{\tfrac{1}{6}} }[/math], [math]\displaystyle{ \sqrt{\tfrac{1}{4}} }[/math], [math]\displaystyle{ \sqrt{\tfrac{1}{4}} }[/math], first from a 16-cell vertex to a 16-cell edge center, then turning 90° to a 16-cell face center, then turning 90° to a 16-cell tetrahedral cell center, then turning 90° to the 16-cell center.
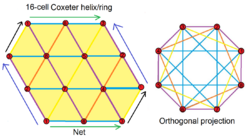
Helical construction

A 16-cell can be constructed (three different ways) from two Boerdijk–Coxeter helixes of eight chained tetrahedra, each bent in the fourth dimension into a ring.[16][17] The two circular helixes spiral around each other, nest into each other and pass through each other forming a Hopf link. The 16 triangle faces can be seen in a 2D net within a triangular tiling, with 6 triangles around every vertex. The purple edges represent the Petrie polygon of the 16-cell. The eight-cell ring of tetrahedra contains three octagrams of different colors, eight-edge circular paths that wind twice around the 16-cell on every third vertex of the octagram. The orange and yellow edges are two four-edge halves of one octagram, which join their ends to form a Möbius strip.
Thus the 16-cell can be decomposed into two cell-disjoint circular chains of eight tetrahedrons each, four edges long, one spiraling to the right (clockwise) and the other spiraling to the left (counterclockwise). The left-handed and right-handed cell rings fit together, nesting into each other and entirely filling the 16-cell, even though they are of opposite chirality. This decomposition can be seen in a 4-4 duoantiprism construction of the 16-cell: ![]()
![]()
![]()
![]()
![]()
![]()
![]() or
or ![]()
![]()
![]()
![]()
![]()
![]()
![]() , Schläfli symbol {2}⨂{2} or s{2}s{2}, symmetry [4,2+,4], order 64.
, Schläfli symbol {2}⨂{2} or s{2}s{2}, symmetry [4,2+,4], order 64.
Three eight-edge paths (of different colors) spiral along each eight-cell ring, making 90° angles at each vertex. (In the Boerdijk–Coxeter helix before it is bent into a ring, the angles in different paths vary, but are not 90°.) Three paths (with three different colors and apparent angles) pass through each vertex. When the helix is bent into a ring, the segments of each eight-edge path (of various lengths) join their ends, forming a Möbius strip eight edges long along its single-sided circumference of 8𝝅, and one edge wide.[lower-alpha 16] The six four-edge halves of the three eight-edge paths each make four 90° angles, but they are not the six orthogonal great squares: they are open-ended squares, four-edge 360° helices whose open ends are antipodal vertices. The four edges come from four different great squares, and are mutually orthogonal. Combined end-to-end in pairs of the same chirality, the six four-edge paths make three eight-edge Möbius loops, helical octagrams. Each octagram is both a Petrie polygon of the 16-cell, and the helical track along which all eight vertices rotate together, in one of the 16-cell's distinct isoclinic rotations.[lower-alpha 23]
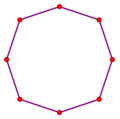
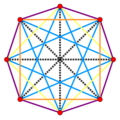
| Five ways of looking at the same skew octagram[lower-alpha 24] | ||||
|---|---|---|---|---|
| Edge path | Petrie polygon[18] | 16-cell | Discrete fibration | Isocline chords |
| Octagram{8/3}[19] | Octagram{8/1} | Coxeter plane B4 | Octagram{8/2}=2{4} | Octagram{8/4}=4{2} |

|
|
|

|

|
| The eight √2 edges of the edge-path of an isocline.[lower-alpha 25] | Skew octagon of eight √2 edges. The 16-cell has 3 of these 8-vertex circuits. | All 24 √2 edges and the four √4 orthogonal axes.[lower-alpha 26] | Two completely orthogonal (disjoint) great squares of √2 edges.[lower-alpha 7] | Eight √4 chords of an isocline (doubled).[lower-alpha 27] |
Each eight-edge helix is a skew octagram{8/3} that winds twice around the 16-cell and visits every vertex before closing into a loop. Its eight edges are the circular path-near-edges of an isocline, a geodesic arc on which vertices move during an isoclinic rotation.[lower-alpha 17] The isoclines connect opposite vertices of face-bonded tetrahedral cells,[lower-alpha 15] which are also opposite vertices (antipodal vertices) of the 16-cell, so the isoclines have √4 chords.[lower-alpha 27] The isocline winds around the 16-cell twice (720°) the way the edges of the octagram{8/3} wind around twice, passing alongside each of the √2 edges once,[lower-alpha 25] and alongside each of the √4 orthogonal axes of the 16-cell twice.[lower-alpha 26] The isocline makes a circle of circumference 8𝝅.[lower-alpha 16]
The eight-cell ring is chiral: there is a right-handed form which spirals clockwise, and a left-handed form which spirals counterclockwise. The 16-cell contains one of each, so it also contains a left and a right isocline; the isocline is the circular axis around which the eight-cell ring twists. Each isocline visits all eight vertices of the 16-cell.[lower-alpha 30] Each eight-cell ring contains half of the 16 cells, but all 8 vertices; the two rings share the vertices, as they nest into each other and fit together. They also share the 24 edges, though left and right octagram helices are different eight-edge paths.[lower-alpha 31]
Because there are three pairs of completely orthogonal great squares,[lower-alpha 3] there are three congruent ways to compose a 16-cell from two eight-cell rings. The 16-cell contains three left-right pairs of eight-cell rings in different orientations, with each cell ring containing its axial isocline.[lower-alpha 23] Each left-right pair of isoclines is the track of a left-right pair of distinct isoclinic rotations: the rotations in one pair of completely orthogonal invariant planes of rotation.[lower-alpha 7] At each vertex, there are three great squares and six octagram isoclines that cross at the vertex and share a 16-cell axis chord.[lower-alpha 32]
As a configuration
This configuration matrix represents the 16-cell. The rows and columns correspond to vertices, edges, faces, and cells. The diagonal numbers say how many of each element occur in the whole 16-cell. The nondiagonal numbers say how many of the column's element occur in or at the row's element.
[math]\displaystyle{ \begin{bmatrix}\begin{matrix}8 & 6 & 12 & 8 \\ 2 & 24 & 4 & 4 \\ 3 & 3 & 32 & 2 \\ 4 & 6 & 4 & 16 \end{matrix}\end{bmatrix} }[/math]
Tessellations
One can tessellate 4-dimensional Euclidean space by regular 16-cells. This is called the 16-cell honeycomb and has Schläfli symbol {3,3,4,3}. Hence, the 16-cell has a dihedral angle of 120°.[21] Each 16-cell has 16 neighbors with which it shares a tetrahedron, 24 neighbors with which it shares only an edge, and 72 neighbors with which it shares only a single point. Twenty-four 16-cells meet at any given vertex in this tessellation.
The dual tessellation, the 24-cell honeycomb, {3,4,3,3}, is made of regular 24-cells. Together with the tesseractic honeycomb {4,3,3,4} these are the only three regular tessellations of R4.
Projections
| Coxeter plane | B4 | B3 / D4 / A2 | B2 / D3 |
|---|---|---|---|
| Graph | 
|
|

|
| Dihedral symmetry | [8] | [6] | [4] |
| Coxeter plane | F4 | A3 | |
| Graph | 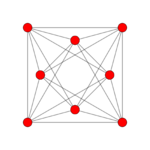
|
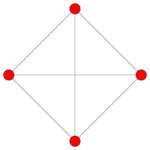
| |
| Dihedral symmetry | [12/3] | [4] |
The cell-first parallel projection of the 16-cell into 3-space has a cubical envelope. The closest and farthest cells are projected to inscribed tetrahedra within the cube, corresponding with the two possible ways to inscribe a regular tetrahedron in a cube. Surrounding each of these tetrahedra are 4 other (non-regular) tetrahedral volumes that are the images of the 4 surrounding tetrahedral cells, filling up the space between the inscribed tetrahedron and the cube. The remaining 6 cells are projected onto the square faces of the cube. In this projection of the 16-cell, all its edges lie on the faces of the cubical envelope.
The cell-first perspective projection of the 16-cell into 3-space has a triakis tetrahedral envelope. The layout of the cells within this envelope are analogous to that of the cell-first parallel projection.
The vertex-first parallel projection of the 16-cell into 3-space has an octahedral envelope. This octahedron can be divided into 8 tetrahedral volumes, by cutting along the coordinate planes. Each of these volumes is the image of a pair of cells in the 16-cell. The closest vertex of the 16-cell to the viewer projects onto the center of the octahedron.
Finally the edge-first parallel projection has a shortened octahedral envelope, and the face-first parallel projection has a hexagonal bipyramidal envelope.
4 sphere Venn diagram
A 3-dimensional projection of the 16-cell and 4 intersecting spheres (a Venn diagram of 4 sets) are topologically equivalent.
|
|
4 sphere Venn diagram and 16-cell projection in the same orientation |
Symmetry constructions
The 16-cell's symmetry group is denoted B4.
There is a lower symmetry form of the 16-cell, called a demitesseract or 4-demicube, a member of the demihypercube family, and represented by h{4,3,3}, and Coxeter diagrams ![]()
![]()
![]()
![]()
![]()
![]()
![]() or
or ![]()
![]()
![]()
![]()
![]() . It can be drawn bicolored with alternating tetrahedral cells.
. It can be drawn bicolored with alternating tetrahedral cells.
It can also be seen in lower symmetry form as a tetrahedral antiprism, constructed by 2 parallel tetrahedra in dual configurations, connected by 8 (possibly elongated) tetrahedra. It is represented by s{2,4,3}, and Coxeter diagram: ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
It can also be seen as a snub 4-orthotope, represented by s{21,1,1}, and Coxeter diagram: ![]()
![]()
![]()
![]()
![]()
![]()
![]() or
or ![]()
![]()
![]()
![]()
![]() .
.
With the tesseract constructed as a 4-4 duoprism, the 16-cell can be seen as its dual, a 4-4 duopyramid.
| Name | Coxeter diagram | Schläfli symbol | Coxeter notation | Order | Vertex figure |
|---|---|---|---|---|---|
| Regular 16-cell | {3,3,4} | [3,3,4] | 384 | ||
| Demitesseract Quasiregular 16-cell |
h{4,3,3} {3,31,1} |
[31,1,1] = [1+,4,3,3] | 192 | ||
| Alternated 4-4 duoprism | 2s{4,2,4} | 4,2+,4 | 64 | ||
| Tetrahedral antiprism | s{2,4,3} | [2+,4,3] | 48 | ||
| Alternated square prism prism | sr{2,2,4} | [(2,2)+,4] | 16 | ||
| Snub 4-orthotope | s{21,1,1} | [2,2,2]+ = [21,1,1]+ | 8 | ||
| 4-fusil | |||||
| {3,3,4} | [3,3,4] | 384 | |||
| {4}+{4} or 2{4} | 4,2,4 = [8,2+,8] | 128 | |||
| {3,4}+{ } | [4,3,2] | 96 | |||
| {4}+2{ } | [4,2,2] | 32 | |||
| { }+{ }+{ }+{ } or 4{ } | [2,2,2] | 16 |
Related complex polygons
The Möbius–Kantor polygon is a regular complex polygon 3{3}3, ![]()
![]()
![]() , in [math]\displaystyle{ \mathbb{C}^2 }[/math] shares the same vertices as the 16-cell. It has 8 vertices, and 8 3-edges.[22][23]
, in [math]\displaystyle{ \mathbb{C}^2 }[/math] shares the same vertices as the 16-cell. It has 8 vertices, and 8 3-edges.[22][23]
The regular complex polygon, 2{4}4, ![]()
![]()
![]() , in [math]\displaystyle{ \mathbb{C}^2 }[/math] has a real representation as a 16-cell in 4-dimensional space with 8 vertices, 16 2-edges, only half of the edges of the 16-cell. Its symmetry is 4[4]2, order 32.[24]
, in [math]\displaystyle{ \mathbb{C}^2 }[/math] has a real representation as a 16-cell in 4-dimensional space with 8 vertices, 16 2-edges, only half of the edges of the 16-cell. Its symmetry is 4[4]2, order 32.[24]
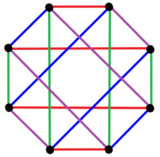 In B4 Coxeter plane, 2{4}4 has 8 vertices and 16 2-edges, shown here with 4 sets of colors. |
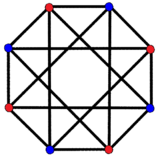 The 8 vertices are grouped in 2 sets (shown red and blue), each only connected with edges to vertices in the other set, making this polygon a complete bipartite graph, K4,4.[25] |
Related uniform polytopes and honeycombs
The regular 16-cell and tesseract are the regular members of a set of 15 uniform 4-polytopes with the same B4 symmetry. The 16-cell is also one of the uniform polytopes of D4 symmetry.
The 16-cell is also related to the cubic honeycomb, order-4 dodecahedral honeycomb, and order-4 hexagonal tiling honeycomb which all have octahedral vertex figures.
It belongs to the sequence of {3,3,p} 4-polytopes which have tetrahedral cells. The sequence includes three regular 4-polytopes of Euclidean 4-space, the 5-cell {3,3,3}, 16-cell {3,3,4}, and 600-cell {3,3,5}), and the order-6 tetrahedral honeycomb {3,3,6} of hyperbolic space.
It is first in a sequence of quasiregular polytopes and honeycombs h{4,p,q}, and a half symmetry sequence, for regular forms {p,3,4}.
See also
Fundamental convex regular and uniform polytopes in dimensions 2–10
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||
Notes
- ↑ The convex regular 4-polytopes can be ordered by size as a measure of 4-dimensional content (hypervolume) for the same radius. Each greater polytope in the sequence is rounder than its predecessor, enclosing more content[5] within the same radius. The 4-simplex (5-cell) is the limit smallest case, and the 120-cell is the largest. Complexity (as measured by comparing configuration matrices or simply the number of vertices) follows the same ordering. This provides an alternative numerical naming scheme for regular polytopes in which the 16-cell is the 8-point 4-polytope: second in the ascending sequence that runs from 5-point 4-polytope to 600-point 4-polytope.
- ↑ There are 2 and only 2 16-cells inscribed in the 8-cell (tesseract), 3 and only 3 16-cells inscribed in the 24-cell, 75 distinct 16-cells (but only 15 disjoint 16-cells) inscribed in the 600-cell, and 675 distinct 16-cells (but only 75 disjoint 16-cells) inscribed in the 120-cell.
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 3.6 In 4 dimensional space we can construct 4 perpendicular axes and 6 perpendicular planes through a point. Without loss of generality, we may take these to be the axes and orthogonal central planes of a (w, x, y, z) Cartesian coordinate system. In 4 dimensions we have the same 3 orthogonal planes (xy, xz, yz) that we have in 3 dimensions, and also 3 others (wx, wy, wz). Each of the 6 orthogonal planes shares an axis with 4 of the others, and is opposite or completely orthogonal to just one of the others: the only one with which it does not share an axis. Thus there are 3 pairs of completely orthogonal planes: xy and wz intersect only at the origin; xz and wy intersect only at the origin; yz and wx intersect only at the origin.
- ↑ 4.0 4.1 4.2 Each vertex in the 16-cell is the apex of an octahedral pyramid, the base of which is the octahedron formed by the 6 other vertices to which the apex is connected by edges. The 16-cell can be deconstructed (four different ways) into two octahedral pyramids by cutting it in half through one of its four octahedral central hyperplanes. Looked at from inside the curved 3 dimensional volume of its boundary surface of 16 face-bonded tetrahedra, the 16-cell's vertex figure is an octahedron. In 4 dimensions, the vertex octahedron is actually an octahedral pyramid. The apex of the octahedral pyramid (the vertex where the 6 edges meet) is not actually at the center of the octahedron: it is displaced radially outwards in the fourth dimension, out of the hyperplane defined by the octahedron's 6 vertices. The 6 edges around the vertex make an orthogonal 3-axis cross in 3 dimensions (and in the 3-dimensional projection of the 4-pyramid), but the 3 lines are actually bent 90 degrees in the fourth dimension where they meet in an apex.
- ↑ The boundary surface of a 16-cell is a finite 3-dimensional space consisting of 16 tetrahedra arranged face-to-face (four around one). It is a closed, tightly curved (non-Euclidean) 3-space, within which we can move straight through 4 tetrahedra in any direction and arrive back in the tetrahedron where we started. We can visualize moving around inside this tetrahedral jungle gym, climbing from one tetrahedron into another on its 24 struts (its edges), and never being able to get out (or see out) of the 16 tetrahedra no matter what direction we go (or look). We are always on (or in) the surface of the 16-cell, never inside the 16-cell itself (nor outside it). We can see that the 6 edges around each vertex radiate symmetrically in 3 dimensions and form an orthogonal 3-axis cross, just as the radii of an octahedron do (so we say the vertex figure of the 16-cell is the octahedron).[lower-alpha 4]
- ↑ 6.0 6.1 6.2 Two flat planes A and B of a Euclidean space of four dimensions are called completely orthogonal if and only if every line in A is orthogonal to every line in B. In that case the planes A and B intersect at a single point O, so that if a line in A intersects with a line in B, they intersect at O. A and B are perpendicular and Clifford parallel.[lower-alpha 3]
- ↑ 7.0 7.1 7.2 7.3 Completely orthogonal great squares are non-intersecting and rotate independently because the great circles on which their vertices lie are Clifford parallel.[lower-alpha 12] They are √2 apart at each pair of nearest vertices (and in the 16-cell all the pairs except antipodal pairs are nearest). The two squares cannot intersect at all because they lie in planes which intersect at only one point: the center of the 16-cell.[lower-alpha 3] Because they are perpendicular and share a common center, the two squares are obviously not parallel and separate in the usual way of parallel squares in 3 dimensions; rather they are connected like adjacent square links in a chain, each passing through the other without intersecting at any points, forming a Hopf link.
- ↑ 8.0 8.1 Three great squares meet at each vertex (and at its opposite vertex) in the 16-cell. Each of them has a different completely orthogonal square.[lower-alpha 6] Thus there are three great squares completely orthogonal to each vertex and its opposite vertex (each axis). They form an octahedron (a central hyperplane). Every axis line in the 16-cell is completely orthogonal to a central octahedron hyperplane, as every great square plane is completely orthogonal to another great square plane.[lower-alpha 3] The axis and the octahedron intersect only at one point (the center of the 16-cell), as each pair of completely orthogonal great squares intersects only at one point (the center of the 16-cell). Each central octahedron is also the octahedral vertex figure of two of the eight vertices: the two on its completely orthogonal axis.
- ↑ The three incompletely orthogonal great squares which intersect at each vertex of the 16-cell form the vertex's octahedral vertex figure.[lower-alpha 4] Any two of them, together with the completely orthogonal square of the third, also form an octahedron: a central octahedral hyperplane.[lower-alpha 8] In the 16-cell, each octahedral vertex figure is also a central octahedral hyperplane.
- ↑ Each great square vertex is √2 distant from two of the square's other vertices, and √4 distant from its opposite vertex. The other four vertices of the 16-cell (also √2 distant) are the vertices of the square's completely orthogonal square.[lower-alpha 7] Each 16-cell vertex is a vertex of three orthogonal great squares which intersect there. Each of them has a different completely orthogonal square. Thus there are three great squares completely orthogonal to each vertex: squares that the vertex is not part of.[lower-alpha 9]
- ↑ 11.0 11.1 11.2 11.3 Each great square plane is isoclinic (Clifford parallel) to five other square planes but completely orthogonal[lower-alpha 6] to only one of them. Every pair of completely orthogonal planes has Clifford parallel great circles, but not all Clifford parallel great circles are orthogonal. There is also another way in which completely orthogonal planes are in a distinguished category of Clifford parallel planes: they are not chiral. A pair of isoclinic (Clifford parallel) planes is either a left pair or a right pair unless they are separated by two angles of 90° (completely orthogonal planes) or 0° (coincident planes).[20] Most isoclinic planes are brought together only by a left isoclinic rotation or a right isoclinic rotation, respectively. Completely orthogonal planes are special: the pair of planes is both a left and a right pair, so either a left or a right isoclinic rotation will bring them together. Because planes separated by a 90° isoclinic rotation are 180° apart, the plane to the left and the plane to the right are the same plane.[lower-alpha 18]
- ↑ 12.0 12.1 12.2 Clifford parallels are non-intersecting curved lines that are parallel in the sense that the perpendicular (shortest) distance between them is the same at each point.[7] A double helix is an example of Clifford parallelism in ordinary 3-dimensional Euclidean space. In 4-space Clifford parallels occur as geodesic great circles on the 3-sphere.[8] In the 16-cell the corresponding vertices of completely orthogonal great circle squares are all √2 apart, so these squares are Clifford parallel polygons.[lower-alpha 11] Note that only the vertices of the great squares (the points on the great circle) are √2 apart; points on the edges of the squares (on chords of the circle) are closer together.
- ↑ 13.0 13.1 Opposite vertices in a unit-radius 4-polytope correspond to the opposite vertices of an 8-cell hypercube (tesseract). The long diagonal of this radially equilateral 4-cube is √4. In a 90° isoclinic rotation each vertex of the 16-cell is displaced to its antipodal vertex, traveling along a helical geodesic arc of length 𝝅 (180°), to a vertex √4 away along the long diameter of the unit-radius 4-polytope (16-cell or tesseract), the same total displacement as if it had been displaced √1 four times by traveling along a path of four successive orthogonal edges of the tesseract.
- ↑ There are six different two-edge paths connecting a pair of antipodal vertices along the edges of a great square. The left isoclinic rotation runs diagonally between three of them, and the right isoclinic rotation runs diagonally between the other three. These diagonals are the straight lines (geodesics) connecting opposite vertices of face-bonded tetrahedral cells in the left-handed eight-cell ring and the right-handed eight-cell ring, respectively.
- ↑ 15.0 15.1 15.2 Successive vertices visited by an isocline are two edges apart along a great circle, in adjacent cells. In the 16-cell they are the opposite vertices of two face-bonded tetrahedral cells. The two vertices are connected by three two-edge great circle paths along edges of the tetrahedra, but the isocline is the shortest path between them: the geodesic path. On the arc of the isocline (a straight line through 3-space) the two vertices are √16/3 ≈ 2.309 apart, compared to the path along the two √2 edges ≈ 2.828. The vertices are only √4 = 2.0 apart in 4-space, because they are antipodal vertices.[lower-alpha 27]
- ↑ 16.0 16.1 16.2 An isocline is a circle of special kind corresponding to a pair of Villarceau circles linked in a Möbius loop. It curves through four dimensions instead of just two. All ordinary circles have a 2𝝅 circumference, but the 16-cell's isocline is a circle with an 8𝝅 circumference (over eight 180° chords). An isocline is a geodesic circle that does not lie in a central plane, but to avoid confusion we always refer to it as an isocline and reserve the term great circle for an ordinary great circle in the plane.
- ↑ 17.0 17.1 17.2 In an isoclinic rotation, all 6 orthogonal planes are displaced in two orthogonal directions at once: they are rotated by the same angle, and at the same time they are tilted sideways by that same angle. An isoclinic displacement (also known as a Clifford displacement) is 4-dimensionally diagonal. Points are displaced an equal distance in four orthogonal directions at once, and displaced a total Pythagorean distance equal to the square root of four times the square of that distance. All vertices of a regular 4-polytope are displaced to a vertex at least two edge lengths away. For example, when the unit-radius 16-cell rotates isoclinically 90° in a great square invariant plane, it also rotates 90° in the completely orthogonal great square invariant plane.[lower-alpha 3] The great square plane also tilts sideways 90° to occupy its completely orthogonal plane. (By isoclinic symmetry, every great square rotates 90° and tilts sideways 90° into its completely orthogonal plane.) Each vertex (in every great square) is displaced to its antipodal vertex, at a distance of √1 in each of four orthogonal directions, a total distance of √4.[lower-alpha 13] The original and displaced vertex are two edge lengths apart by three[lower-alpha 14] different paths along two edges of a great square. But the isocline (the geodesic arc the vertex follows during the isoclinic rotation) does not run along edges: it runs between these different edge-paths diagonally, on a geodesic (shortest arc) between the original and displaced vertices.[lower-alpha 15] This isoclinic geodesic arc is not a segment of an ordinary great circle; it does not lie in the plane of any great square. It is a helical 180° arc that bends in a circle in two completely orthogonal planes at once. This Möbius circle does not lie in any plane or intersect any vertices between the original and the displaced vertex.[lower-alpha 16]
- ↑ 18.0 18.1 18.2 The 90 degree isoclinic rotation of two completely orthogonal planes takes them to each other. In such a rotation of a rigid 16-cell, all 6 orthogonal planes rotate by 90 degrees, and also tilt sideways by 90 degrees to their completely orthogonal (Clifford parallel)[lower-alpha 12] plane.[9] The corresponding vertices of the two completely orthogonal great squares are √4 (180°) apart; the great squares (Clifford parallel polytopes) are √4 (180°) apart; but the two completely orthogonal planes are 90° apart, in the two orthogonal angles that separate them. If the isoclinic rotation is continued through another 90°, each vertex completes a 360° rotation and each great square returns to its original plane, but in a different orientation (axes swapped): it has been turned "upside down" on the surface of the 16-cell (which is now "inside out"). Continuing through a second 360° isoclinic rotation (through four 90° by 90° isoclinic steps, a 720° rotation) returns everything to its original place and orientation.
- ↑ An orthoscheme is a chiral irregular simplex with right triangle faces that is characteristic of some polytope if it will exactly fill that polytope with the reflections of itself in its own facets (its mirror walls). Every regular polytope can be dissected radially into instances of its characteristic orthoscheme surrounding its center. The characteristic orthoscheme has the shape described by the same Coxeter-Dynkin diagram as the regular polytope without the generating point ring.
- ↑ A regular polytope of dimension k has a characteristic k-orthoscheme, and also a characteristic (k-1)-orthoscheme. A regular 4-polytope has a characteristic 5-cell (4-orthoscheme) into which it is subdivided by its (3-dimensional) hyperplanes of symmetry, and also a characteristic tetrahedron (3-orthoscheme) into which its surface is subdivided by its cells' (2-dimensional) planes of symmetry. After subdividing its (3-dimensional) surface into characteristic tetrahedra surrounding each cell center, its (4-dimensional) interior can be subdivided into characteristic 5-cells by adding radii joining the vertices of the surface characteristic tetrahedra to the 4-polytope's center.[12] The interior tetrahedra and triangles thus formed will also be orthoschemes.
- ↑ 21.0 21.1 (Coxeter 1973) uses the greek letter 𝝓 (phi) to represent one of the three characteristic angles 𝟀, 𝝓, 𝟁 of a regular polytope. Because 𝝓 is commonly used to represent the golden ratio constant ≈ 1.618, for which Coxeter uses 𝝉 (tau), we reverse Coxeter's conventions, and use 𝝉 to represent the characteristic angle.
- ↑ The four edges of each 4-orthoscheme which meet at the center of a regular 4-polytope are of unequal length, because they are the four characteristic radii of the regular 4-polytope: a vertex radius, an edge center radius, a face center radius, and a cell center radius. The five vertices of the 4-orthoscheme always include one regular 4-polytope vertex, one regular 4-polytope edge center, one regular 4-polytope face center, one regular 4-polytope cell center, and the regular 4-polytope center. Those five vertices (in that order) comprise a path along four mutually perpendicular edges (that makes three right angle turns), the characteristic feature of a 4-orthoscheme. The 4-orthoscheme has five dissimilar 3-orthoscheme facets.
- ↑ 23.0 23.1 The 16-cell can be constructed from two cell-disjoint eight-cell rings in three different ways; it has three orientations of its pair of rings. Each orientation "contains" a distinct left-right pair of isoclinic rotations, and also a pair of completely orthogonal great squares (Clifford parallel fibers), so each orientation is a discrete fibration of the 16-cell. Each eight-cell ring contains three axial octagrams which have different orientations (they exchange roles) in the three discrete fibrations and six distinct isoclinic rotations (three left and three right) through the cell rings. Three octagrams (of different colors) can be seen in the illustration of a single cell ring, one in the role of Petrie polygon, one as the right isocline, and one as the left isocline. Because each octagram plays three roles, there are exactly six distinct isoclines in the 16-cell, not 18.
- ↑ All five views are the same orthogonal projection of the 16-cell into the same plane (a circular cross-section of the eight-cell ring cylinder), looking along the central axis of the cut ring cylinder pictured above, from one end of the cylinder. The only difference is which √2 edges and √4 isocline chords are omitted for focus. The different colors of √2 edges appear to be of different lengths because they are oblique to the viewer at different angles. Vertices are numbered 1 (top) through 8 in counterclockwise order.
- ↑ 25.0 25.1 25.2 25.3 There is a path between any two adjacent isocline vertices along four mutually orthogonal √2 edges, making three left 90° turns or three right 90° turns, and thus forming an open square (a square helix). This roundabout path is characteristic of the isocline because the helical arc over the √4 chord curves along it, missing the three vertices on it. These four-edge paths can be seen in a regular octagram{8/3} in which eight √2 edges wind twice around the 16-cell under their invisible 90° isocline arc segments. Notice that the endpoints of four-edge path segments are antipodal vertices (connected by a √4 chord).
- ↑ 26.0 26.1 Each isocline has the eight √2 edges of its edge-path, and eight √4 chords that connect every 3rd vertex on the hexagram{8/3}, vertices that have a twisted path of four mutually orthogonal √2 edges connecting them. The isocline curves smoothly around in a helix, over the √4 chord, and alongside the four orthogonal √2 edges of the edge-path, but it does not actually touch the three vertices of that four-edge path where it makes sharp right-angled turns.[lower-alpha 25] Each √2 edge is an edge of a great square, that is completely orthogonal to another great square, in which the √4 chord is a diagonal.
- ↑ 27.0 27.1 27.2 Successive vertices visited by an isocline are √4 apart in 4-space because they are antipodal vertices.[lower-alpha 13] The isocline's √4 chords can be seen in an octagram4{2} running straight through the center of the 16-cell under their invisible 180° isocline arcs. Each orthogonal axis is used twice as a chord in each 8-chord isocline. The two uses of each axis have different (but congruent) 180° isocline arcs: each 180° arc is a helical half-circle path that winds around alongside a unique four-edge path of hexagram{8/3} edges.[lower-alpha 25] The two half-circles have the same chirality (they both wind either clockwise or counterclockwise), so the isocline can be made by nesting the two half-circle helices together to form a circular double helix, and joining the open ends of the two half-circles together to make a Möbius strip whose "single edge" runs through all eight vertices. The two half-circle arcs are completely orthogonal (all their corresponding points are 180° apart), but their chords are coincident (the same √4 axis).
- ↑ 28.0 28.1 For another example of the left and right isoclines of a rotation visiting the same set of vertices, see the characteristic isoclinic rotation of the 5-cell. Although in these two special cases left and right isoclines of the same rotation visit the same set of vertices, they still take very different rotational paths because they visit the same vertices in different sequences.
- ↑ 29.0 29.1 Except in the 5-cell and 16-cell,[lower-alpha 28] a pair of left and right isocline circles have disjoint vertices: the left and right isocline helices are non-intersecting parallels but counter-rotating, forming a special kind of double helix which cannot occur in three dimensions (where counter-rotating helices of the same radius must intersect).
- ↑ 30.0 30.1 In the 16-cell each single isocline winds through all 8 vertices: an entire fibration of two completely orthogonal great squares.[lower-alpha 11] The 5-cell and the 16-cell are the only regular 4-polytopes where each discrete fibration has just one isocline fiber.[lower-alpha 29]
- ↑ The left and right isoclines intersect each other at every vertex; but with respect to a different set of vertex pairs which are √2 apart, they can be considered to be Clifford parallel. There is also a sense in which they are completely orthogonal.[lower-alpha 11]
- ↑ This is atypical for isoclinic rotations generally; normally both the left and right isoclines do not occur at the same vertex: there are two disjoint sets of vertices reachable only by the left or right rotation respectively.[lower-alpha 29] The left and right isoclines of the 16-cell form a very special double helix: unusual not just because it is circular, but because its different left and right helices twist around each other through the same set of antipodal vertices,[lower-alpha 30] not through the two disjoint subsets of antipodal vertices, as the isocline pairs do in most isoclinic rotations found in nature.[lower-alpha 28] Isoclinic rotations in completely orthogonal invariant planes are special.[lower-alpha 11] To see how and why they are special, visualize two completely orthogonal invariant planes of rotation, each rotating by some rotation angle and tilting sideways by the same rotation angle into a different plane entirely.[lower-alpha 17] Only when the rotation angle is 90°, that different plane in which the tilting invariant plane lands will be the completely orthogonal invariant plane itself. The destination plane of the rotation is the completely orthogonal invariant plane. The 90° isoclinic rotation is the only rotation which takes the completely orthogonal invariant planes to each other.[lower-alpha 18] This reciprocity is the reason both left and right rotations go to the same place.
Citations
- ↑ Coxeter 1973, p. 141, § 7-x. Historical remarks.
- ↑ N.W. Johnson: Geometries and Transformations, (2018) ISBN:978-1-107-10340-5 Chapter 11: Finite Symmetry Groups, 11.5 Spherical Coxeter groups, p.249
- ↑ Matila Ghyka, The Geometry of Art and Life (1977), p.68
- ↑ Coxeter 1973, pp. 120=121, § 7.2. See illustration Fig 7.2B.
- ↑ Coxeter 1973, pp. 292-293, Table I(ii): The sixteen regular polytopes {p,q,r} in four dimensions; An invaluable table providing all 20 metrics of each 4-polytope in edge length units. They must be algebraically converted to compare polytopes of unit radius.
- ↑ Kim & Rote 2016, p. 6, § 5. Four-Dimensional Rotations.
- ↑ Tyrrell & Semple 1971, pp. 5-6, § 3. Clifford's original definition of parallelism.
- ↑ Kim & Rote 2016, pp. 7-10, § 6. Angles between two Planes in 4-Space.
- ↑ Kim & Rote 2016, pp. 8-10, Relations to Clifford Parallelism.
- ↑ Coxeter 1973, p. 121, § 7.21. See illustration Fig 7.2B: "[math]\displaystyle{ \beta_4 }[/math] is a four-dimensional dipyramid based on [math]\displaystyle{ \beta_3 }[/math] (with its two apices in opposite directions along the fourth dimension)."
- ↑ Tyrrell & Semple 1971.
- ↑ Coxeter 1973, p. 130, § 7.6; "simplicial subdivision".
- ↑ Coxeter 1973, pp. 292-293, Table I(ii); "16-cell, 𝛽4".
- ↑ Coxeter 1973, p. 139, § 7.9 The characteristic simplex.
- ↑ Coxeter 1973, p. 290, Table I(ii); "dihedral angles".
- ↑ Coxeter 1970, p. 45, Table 2: Reflexible honeycombs and their groups; Honeycomb [3,3,4]4 is a tiling of the 3-sphere by 2 rings of 8 tetrahedral cells.
- ↑ Banchoff 2013.
- ↑ Coxeter 1973, pp. 292-293, Table I(ii); 24-cell h1.
- ↑ Coxeter 1973, pp. 292-293, Table I(ii); 24-cell h2.
- ↑ Kim & Rote 2016, pp. 7-8, § 6 Angles between two Planes in 4-Space; Left and Right Pairs of Isoclinic Planes.
- ↑ Coxeter 1973, p. 293.
- ↑ Coxeter 1991, pp. 30,47.
- ↑ Coxeter & Shephard 1992.
- ↑ Coxeter 1991, p. 108.
- ↑ Coxeter 1991, p. 114.
References
- T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- H.S.M. Coxeter:
- Coxeter, H.S.M. (1973). Regular Polytopes (3rd ed.). New York: Dover.
- Coxeter, H.S.M. (1991). Regular Complex Polytopes (2nd ed.). Cambridge: Cambridge University Press.
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN:978-0-471-01003-6 Kaleidoscopes: Selected Writings of H.S.M. Coxeter | Wiley
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Coxeter, H.S.M.; Shephard, G.C. (1992). "Portraits of a family of complex polytopes". Leonardo 25 (3/4): 239–244. doi:10.2307/1575843.
- Coxeter, H.S.M. (1970), "Twisted Honeycombs", Conference Board of the Mathematical Sciences Regional Conference Series in Mathematics (Providence, Rhode Island: American Mathematical Society) 4
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN:978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1n1)
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
- Kim, Heuna; Rote, Günter (2016). "Congruence Testing of Point Sets in 4 Dimensions". arXiv:1603.07269 [cs.CG].
- Tyrrell, J. A.; Semple, J.G. (1971). Generalized Clifford parallelism. Cambridge University Press. ISBN 0-521-08042-8. https://archive.org/details/generalizedcliff0000tyrr.
- Banchoff, Thomas F. (2013). "Torus Decompostions of Regular Polytopes in 4-space". in Senechal, Marjorie. Shaping Space. Springer New York. pp. 257–266. doi:10.1007/978-0-387-92714-5_20. ISBN 978-0-387-92713-8. https://archive.org/details/shapingspaceexpl00sene.
External links
- Weisstein, Eric W.. "16-Cell". http://mathworld.wolfram.com/16-Cell.html.
- Der 16-Zeller (16-cell) Marco Möller's Regular polytopes in R4 (German)
- Description and diagrams of 16-cell projections
- Klitzing, Richard. "4D uniform polytopes (polychora) x3o3o4o – hex". https://bendwavy.org/klitzing/dimensions/polychora.htm.
 |