Schulz–Zimm distribution
|
Probability density function 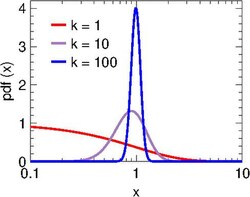 | |||
| Parameters | [math]\displaystyle{ k }[/math] (shape parameter) | ||
|---|---|---|---|
| Support | [math]\displaystyle{ x\in\mathbb{R}_{\gt 0} }[/math] | ||
| [math]\displaystyle{ \frac{k^k x^{k - 1} e^{-kx}}{\Gamma(k)} }[/math] | |||
| Mean | [math]\displaystyle{ 1 }[/math] | ||
| Variance | [math]\displaystyle{ \frac{1}{k} }[/math] | ||
The Schulz–Zimm distribution is a special case of the gamma distribution. It is widely used to model the polydispersity of polymers. In this context it has been introduced in 1939 by Günter Victor Schulz[1] and in 1948 by Bruno H. Zimm.[2]
This distribution has only a shape parameter k, the scale being fixed at θ=1/k. Accordingly, the probability density function is [math]\displaystyle{ f(x)=\frac{k^k x^{k - 1} e^{-kx}}{\Gamma(k)}. }[/math]
When applied to polymers, the variable x is the relative mass or chain length [math]\displaystyle{ x=M/M_n }[/math]. Accordingly, the mass distribution [math]\displaystyle{ f(M) }[/math] is just a gamma distribution with scale parameter [math]\displaystyle{ \theta=M_n/k }[/math]. This explains why the Schulz–Zimm distribution is unheard of outside its conventional application domain.
The distribution has mean 1 and variance 1/k. The polymer dispersity is [math]\displaystyle{ \langle x^2\rangle / \langle x\rangle = 1+1/k }[/math].
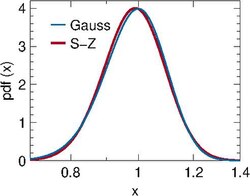
For large k the Schulz–Zimm distribution approaches a Gaussian distribution. In algorithms where one needs to draw samples [math]\displaystyle{ x\ge 0 }[/math], the Schulz–Zimm distribution is to be preferred over a Gaussian because the latter requires an arbitrary cut-off to prevent negative x.
References
- ↑ G V Schulz (1939), Z. Phys. Chem. 43B, 25-46. - Eq (27a) with -ln(a), k+1 in place of our x,k.
- ↑ B H Zimm (1948), J. Chem. Phys. 16, 1099. - Proposes a two-parameter variant of Eq (13) without derivation and without reference to Schulz or whomsoever. One of the two parameters can be eliminated by the requirement <n>=1.
 |