Expected value

Short description: Average value of a random variable

In probability theory, the expected value (also called expectation, expectancy, expectation operator, mathematical expectation, mean, expectation value, or first moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean of the possible values a random variable can take, weighted by the probability of those outcomes. Since it is obtained through arithmetic, the expected value sometimes may not even be included in the sample data set; it is not the value you would "expect" to get in reality.

The expected value of a random variable with a finite number of outcomes is a weighted average of all possible outcomes. In the case of a continuum of possible outcomes, the expectation is defined by integration. In the axiomatic foundation for probability provided by measure theory, the expectation is given by Lebesgue integration.

The expected value of a random variable X is often denoted by E(X), E[X], or EX, with E also often stylized as E or [math]\displaystyle{ \mathbb{E}. }[/math]

History

The idea of the expected value originated in the middle of the 17th century from the study of the so-called problem of points, which seeks to divide the stakes in a fair way between two players, who have to end their game before it is properly finished. This problem had been debated for centuries. Many conflicting proposals and solutions had been suggested over the years when it was posed to Blaise Pascal by French writer and amateur mathematician Chevalier de Méré in 1654. Méré claimed that this problem couldn't be solved and that it showed just how flawed mathematics was when it came to its application to the real world. Pascal, being a mathematician, was provoked and determined to solve the problem once and for all.

He began to discuss the problem in the famous series of letters to Pierre de Fermat. Soon enough, they both independently came up with a solution. They solved the problem in different computational ways, but their results were identical because their computations were based on the same fundamental principle. The principle is that the value of a future gain should be directly proportional to the chance of getting it. This principle seemed to have come naturally to both of them. They were very pleased by the fact that they had found essentially the same solution, and this in turn made them absolutely convinced that they had solved the problem conclusively; however, they did not publish their findings. They only informed a small circle of mutual scientific friends in Paris about it.

In Dutch mathematician Christiaan Huygens' book, he considered the problem of points, and presented a solution based on the same principle as the solutions of Pascal and Fermat. Huygens published his treatise in 1657, (see Huygens (1657)) "De ratiociniis in ludo aleæ" on probability theory just after visiting Paris. The book extended the concept of expectation by adding rules for how to calculate expectations in more complicated situations than the original problem (e.g., for three or more players), and can be seen as the first successful attempt at laying down the foundations of the theory of probability.

In the foreword to his treatise, Huygens wrote:

It should be said, also, that for some time some of the best mathematicians of France have occupied themselves with this kind of calculus so that no one should attribute to me the honour of the first invention. This does not belong to me. But these savants, although they put each other to the test by proposing to each other many questions difficult to solve, have hidden their methods. I have had therefore to examine and go deeply for myself into this matter by beginning with the elements, and it is impossible for me for this reason to affirm that I have even started from the same principle. But finally I have found that my answers in many cases do not differ from theirs.

During his visit to France in 1655, Huygens learned about de Méré's Problem. From his correspondence with Carcavine a year later (in 1656), he realized his method was essentially the same as Pascal's. Therefore, he knew about Pascal's priority in this subject before his book went to press in 1657.

In the mid-nineteenth century, Pafnuty Chebyshev became the first person to think systematically in terms of the expectations of random variables.

Etymology

Neither Pascal nor Huygens used the term "expectation" in its modern sense. In particular, Huygens writes:

That any one Chance or Expectation to win any thing is worth just such a Sum, as wou'd procure in the same Chance and Expectation at a fair Lay. ... If I expect a or b, and have an equal chance of gaining them, my Expectation is worth (a+b)/2.

More than a hundred years later, in 1814, Pierre-Simon Laplace published his tract "Théorie analytique des probabilités", where the concept of expected value was defined explicitly:

… this advantage in the theory of chance is the product of the sum hoped for by the probability of obtaining it; it is the partial sum which ought to result when we do not wish to run the risks of the event in supposing that the division is made proportional to the probabilities. This division is the only equitable one when all strange circumstances are eliminated; because an equal degree of probability gives an equal right for the sum hoped for. We will call this advantage mathematical hope.

Notations

The use of the letter E to denote "expected value" goes back to W. A. Whitworth in 1901. The symbol has since become popular for English writers. In German, E stands for Erwartungswert, in Spanish for esperanza matemática, and in French for espérance mathématique.

When "E" is used to denote "expected value", authors use a variety of stylizations: the expectation operator can be stylized as E (upright), E (italic), or [math]\displaystyle{ \mathbb{E} }[/math] (in blackboard bold), while a variety of bracket notations (such as E(X), E[X], and EX) are all used.

Another popular notation is μ_X, whereas ⟨X⟩, ⟨X⟩_av, and [math]\displaystyle{ \overline{X} }[/math] are commonly used in physics,({{{1}}}, {{{2}}}) and M(X) in Russian-language literature.

Definition

As discussed above, there are several context-dependent ways of defining the expected value. The simplest and original definition deals with the case of finitely many possible outcomes, such as in the flip of a coin. With the theory of infinite series, this can be extended to the case of countably many possible outcomes. It is also very common to consider the distinct case of random variables dictated by (piecewise-)continuous probability density functions, as these arise in many natural contexts. All of these specific definitions may be viewed as special cases of the general definition based upon the mathematical tools of measure theory and Lebesgue integration, which provide these different contexts with an axiomatic foundation and common language.

Any definition of expected value may be extended to define an expected value of a multidimensional random variable, i.e. a random vector X. It is defined component by component, as E[X]_i = E[X_i]. Similarly, one may define the expected value of a random matrix X with components X_ij by E[X]_ij = E[X_ij].

Random variables with finitely many outcomes

Consider a random variable X with a finite list x₁, ..., x_k of possible outcomes, each of which (respectively) has probability p₁, ..., p_k of occurring. The expectation of X is defined as({{{1}}}, {{{2}}})

[math]\displaystyle{ \operatorname{E}[X] =x_1p_1 + x_2p_2 + \cdots + x_kp_k. }[/math]

Since the probabilities must satisfy p₁ + ⋅⋅⋅ + p_k = 1, it is natural to interpret E[X] as a weighted average of the x_i values, with weights given by their probabilities p_i.

In the special case that all possible outcomes are equiprobable (that is, p₁ = ⋅⋅⋅ = p_k), the weighted average is given by the standard average. In the general case, the expected value takes into account the fact that some outcomes are more likely than others.

Examples

An illustration of the convergence of sequence averages of rolls of a die to the expected value of 3.5 as the number of rolls (trials) grows

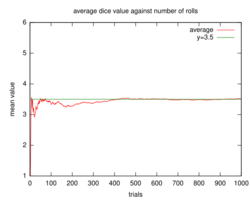
• Let [math]\displaystyle{ X }[/math] represent the outcome of a roll of a fair six-sided die. More specifically, [math]\displaystyle{ X }[/math] will be the number of pips showing on the top face of the die after the toss. The possible values for [math]\displaystyle{ X }[/math] are 1, 2, 3, 4, 5, and 6, all of which are equally likely with a probability of 1/6. The expectation of [math]\displaystyle{ X }[/math] is

[math]\displaystyle{ \operatorname{E}[X] = 1\cdot\frac16 + 2\cdot\frac16 + 3\cdot\frac16 + 4\cdot\frac16 + 5\cdot\frac16 + 6\cdot\frac16 = 3.5. }[/math]

If one rolls the die [math]\displaystyle{ n }[/math] times and computes the average (arithmetic mean) of the results, then as [math]\displaystyle{ n }[/math] grows, the average will almost surely converge to the expected value, a fact known as the strong law of large numbers.

• The roulette game consists of a small ball and a wheel with 38 numbered pockets around the edge. As the wheel is spun, the ball bounces around randomly until it settles down in one of the pockets. Suppose random variable [math]\displaystyle{ X }[/math] represents the (monetary) outcome of a $1 bet on a single number ("straight up" bet). If the bet wins (which happens with probability 1/38 in American roulette), the payoff is $35; otherwise the player loses the bet. The expected profit from such a bet will be

[math]\displaystyle{ \operatorname{E}[\,\text{gain from }\$1\text{ bet}\,] = -\$1 \cdot \frac{37}{38} + \$35 \cdot \frac{1}{38} = -\$\frac{1}{19}. }[/math]

That is, the expected value to be won from a $1 bet is −$1/19. Thus, in 190 bets, the net loss will probably be about $10.

Random variables with countably infinitely many outcomes

Informally, the expectation of a random variable with a countably infinite set of possible outcomes is defined analogously as the weighted average of all possible outcomes, where the weights are given by the probabilities of realizing each given value. This is to say that

[math]\displaystyle{ \operatorname{E}[X] = \sum_{i=1}^\infty x_i\, p_i, }[/math]

where x₁, x₂, ... are the possible outcomes of the random variable X and p₁, p₂, ... are their corresponding probabilities. In many non-mathematical textbooks, this is presented as the full definition of expected values in this context.({{{1}}}, {{{2}}})

However, there are some subtleties with infinite summation, so the above formula is not suitable as a mathematical definition. In particular, the Riemann series theorem of mathematical analysis illustrates that the value of certain infinite sums involving positive and negative summands depends on the order in which the summands are given. Since the outcomes of a random variable have no naturally given order, this creates a difficulty in defining expected value precisely.

For this reason, many mathematical textbooks only consider the case that the infinite sum given above converges absolutely, which implies that the infinite sum is a finite number independent of the ordering of summands.({{{1}}}, {{{2}}}) In the alternative case that the infinite sum does not converge absolutely, one says the random variable does not have finite expectation.({{{1}}}, {{{2}}})

Examples

• Suppose [math]\displaystyle{ x_i = i }[/math] and [math]\displaystyle{ p_i = \tfrac{c}{i2^i} }[/math] for [math]\displaystyle{ i = 1, 2, 3, \ldots, }[/math] where [math]\displaystyle{ c = \tfrac{1}{\ln 2} }[/math] is the scaling factor which makes the probabilities sum to 1. Then we have [math]\displaystyle{ \operatorname{E}[X] \,= \sum_i x_i p_i = 1(\tfrac{c}{2}) + 2(\tfrac{c}{8}) + 3 (\tfrac{c}{24}) + \cdots \,= \, \tfrac{c}{2} + \tfrac{c}{4} + \tfrac{c}{8} + \cdots \,=\, c \,=\, \tfrac{1}{\ln 2}. }[/math]

Random variables with density

Now consider a random variable X which has a probability density function given by a function f on the real number line. This means that the probability of X taking on a value in any given open interval is given by the integral of f over that interval. The expectation of X is then given by the integral({{{1}}}, {{{2}}})

[math]\displaystyle{ \operatorname{E}[X] = \int_{-\infty}^\infty x f(x)\, dx. }[/math]

A general and mathematically precise formulation of this definition uses measure theory and Lebesgue integration, and the corresponding theory of absolutely continuous random variables is described in the next section. The density functions of many common distributions are piecewise continuous, and as such the theory is often developed in this restricted setting.({{{1}}}, {{{2}}}) For such functions, it is sufficient to only consider the standard Riemann integration. Sometimes continuous random variables are defined as those corresponding to this special class of densities, although the term is used differently by various authors.

Analogously to the countably-infinite case above, there are subtleties with this expression due to the infinite region of integration. Such subtleties can be seen concretely if the distribution of X is given by the Cauchy distribution Cauchy(0, π), so that f(x) = (x² + π²)⁻¹. It is straightforward to compute in this case that

[math]\displaystyle{ \int_a^b xf(x)\,dx=\int_a^b \frac{x}{x^2+\pi^2}\,dx=\frac{1}{2}\ln\frac{b^2+\pi^2}{a^2+\pi^2}. }[/math]

The limit of this expression as a → −∞ and b → ∞ does not exist: if the limits are taken so that a = −b, then the limit is zero, while if the constraint 2a = −b is taken, then the limit is ln(2).

To avoid such ambiguities, in mathematical textbooks it is common to require that the given integral converges absolutely, with E[X] left undefined otherwise.({{{1}}}, {{{2}}}) However, measure-theoretic notions as given below can be used to give a systematic definition of E[X] for more general random variables X.

Arbitrary real-valued random variables

All definitions of the expected value may be expressed in the language of measure theory. In general, if X is a real-valued random variable defined on a probability space (Ω, Σ, P), then the expected value of X, denoted by E[X], is defined as the Lebesgue integral({{{1}}}, {{{2}}})

[math]\displaystyle{ \operatorname{E} [X] = \int_\Omega X\,d\operatorname{P}. }[/math]

Despite the newly abstract situation, this definition is extremely similar in nature to the very simplest definition of expected values, given above, as certain weighted averages. This is because, in measure theory, the value of the Lebesgue integral of X is defined via weighted averages of approximations of X which take on finitely many values.({{{1}}}, {{{2}}}) Moreover, if given a random variable with finitely or countably many possible values, the Lebesgue theory of expectation is identical with the summation formulas given above. However, the Lebesgue theory clarifies the scope of the theory of probability density functions. A random variable X is said to be absolutely continuous if any of the following conditions are satisfied:

• there is a nonnegative measurable function f on the real line such that

[math]\displaystyle{ \text{P}(X\in A)=\int_A f(x)\,dx, }[/math]

for any Borel set A, in which the integral is Lebesgue.

• the cumulative distribution function of X is absolutely continuous.
• for any Borel set A of real numbers with Lebesgue measure equal to zero, the probability of X being valued in A is also equal to zero
• for any positive number ε there is a positive number δ such that: if A is a Borel set with Lebesgue measure less than δ, then the probability of X being valued in A is less than ε.

These conditions are all equivalent, although this is nontrivial to establish.({{{1}}}, {{{2}}}) In this definition, f is called the probability density function of X (relative to Lebesgue measure). According to the change-of-variables formula for Lebesgue integration,({{{1}}}, {{{2}}}) combined with the law of the unconscious statistician,({{{1}}}, {{{2}}}) it follows that

[math]\displaystyle{ \operatorname{E}[X]\equiv\int_\Omega X\,d\operatorname{P}=\int_{\mathbb{R}}xf(x)\,dx }[/math]

for any absolutely continuous random variable X. The above discussion of continuous random variables is thus a special case of the general Lebesgue theory, due to the fact that every piecewise-continuous function is measurable.

The expected value of any real-valued random variable [math]\displaystyle{ X }[/math] can also be defined on the graph of its cumulative distribution function [math]\displaystyle{ F }[/math] by a nearby equality of areas. In fact, [math]\displaystyle{ \operatorname{E}[X] = \mu }[/math] with a real number [math]\displaystyle{ \mu }[/math] if and only if the two surfaces in the [math]\displaystyle{ x }[/math]-[math]\displaystyle{ y }[/math]-plane, described by

[math]\displaystyle{ x\le\mu,\;\, 0\le y\le F(x) \quad }[/math] or [math]\displaystyle{ \quad x\ge\mu,\;\, F(x)\le y\le 1 }[/math]

respectively, have the same finite area, i.e. if

[math]\displaystyle{ \int_{-\infty}^\mu F(x)\,dx = \int_\mu^\infty \big(1 - F(x)\big)\,dx }[/math]

and both improper Riemann integrals converge. Finally, this is equivalent to the representation

[math]\displaystyle{ \operatorname{E}[X] = \int_0^\infty \big(1 - F(x)\big)\,dx - \int_{-\infty}^0 F(x)\,dx, }[/math]

also with convergent integrals.({{{1}}}, {{{2}}})

Infinite expected values

Expected values as defined above are automatically finite numbers. However, in many cases it is fundamental to be able to consider expected values of ±∞. This is intuitive, for example, in the case of the St. Petersburg paradox, in which one considers a random variable with possible outcomes x_i = 2ⁱ, with associated probabilities p_i = 2⁻ⁱ, for i ranging over all positive integers. According to the summation formula in the case of random variables with countably many outcomes, one has [math]\displaystyle{ \operatorname{E}[X]= \sum_{i=1}^\infty x_i\,p_i =2\cdot \frac{1}{2}+4\cdot\frac{1}{4} + 8\cdot\frac{1}{8}+ 16\cdot\frac{1}{16}+ \cdots = 1 + 1 + 1 + 1 + \cdots. }[/math] It is natural to say that the expected value equals +∞.

There is a rigorous mathematical theory underlying such ideas, which is often taken as part of the definition of the Lebesgue integral.({{{1}}}, {{{2}}}) The first fundamental observation is that, whichever of the above definitions are followed, any nonnegative random variable whatsoever can be given an unambiguous expected value; whenever absolute convergence fails, then the expected value can be defined as +∞. The second fundamental observation is that any random variable can be written as the difference of two nonnegative random variables. Given a random variable X, one defines the positive and negative parts by X ⁺ = max(X, 0) and X ⁻ = −min(X, 0). These are nonnegative random variables, and it can be directly checked that X = X ⁺ − X ⁻. Since E[X ⁺] and E[X ⁻] are both then defined as either nonnegative numbers or +∞, it is then natural to define: [math]\displaystyle{ \operatorname{E}[X] = \begin{cases} \operatorname{E}[X^+] - \operatorname{E}[X^-] & \text{if } \operatorname{E}[X^+] \lt \infty \text{ and } \operatorname{E}[X^-] \lt \infty;\\ +\infty & \text{if } \operatorname{E}[X^+] = \infty \text{ and } \operatorname{E}[X^-] \lt \infty;\\ -\infty & \text{if } \operatorname{E}[X^+] \lt \infty \text{ and } \operatorname{E}[X^-] = \infty;\\ \text{undefined} & \text{if } \operatorname{E}[X^+] = \infty \text{ and } \operatorname{E}[X^-] = \infty. \end{cases} }[/math]

According to this definition, E[X] exists and is finite if and only if E[X ⁺] and E[X ⁻] are both finite. Due to the formula |X| = X ⁺ + X ⁻, this is the case if and only if E|X| is finite, and this is equivalent to the absolute convergence conditions in the definitions above. As such, the present considerations do not define finite expected values in any cases not previously considered; they are only useful for infinite expectations.

• In the case of the St. Petersburg paradox, one has X ⁻ = 0 and so E[X] = +∞ as desired.
• Suppose the random variable X takes values 1, −2,3, −4, ... with respective probabilities 6π⁻², 6(2π)⁻², 6(3π)⁻², 6(4π)⁻², .... Then it follows that X ⁺ takes value 2k−1 with probability 6((2k−1)π)⁻² for each positive integer k, and takes value 0 with remaining probability. Similarly, X ⁻ takes value 2k with probability 6(2kπ)⁻² for each positive integer k and takes value 0 with remaining probability. Using the definition for non-negative random variables, one can show that both E[X ⁺] = ∞ and E[X ⁻] = ∞ (see Harmonic series). Hence, in this case the expectation of X is undefined.
• Similarly, the Cauchy distribution, as discussed above, has undefined expectation.

Expected values of common distributions

The following table gives the expected values of some commonly occurring probability distributions. The third column gives the expected values both in the form immediately given by the definition, as well as in the simplified form obtained by computation therefrom. The details of these computations, which are not always straightforward, can be found in the indicated references.

Distribution	Notation	Mean E(X)
Bernoulli({{{1}}}, {{{2}}})	[math]\displaystyle{ X \sim~ b(1,p) }[/math]	[math]\displaystyle{ 0\cdot(1-p)+1\cdot p=p }[/math]
Binomial({{{1}}}, {{{2}}})	[math]\displaystyle{ X \sim B(n,p) }[/math]	[math]\displaystyle{ \sum_{i=0}^n i{n\choose i}p^i(1-p)^{n-i}=np }[/math]
Poisson({{{1}}}, {{{2}}})	[math]\displaystyle{ X \sim \mathrm{Po}(\lambda) }[/math]	[math]\displaystyle{ \sum_{i=0}^\infty \frac{ie^{-\lambda}\lambda^i}{i!}=\lambda }[/math]
Geometric({{{1}}}, {{{2}}})	[math]\displaystyle{ X \sim \mathrm{Geometric}(p) }[/math]	[math]\displaystyle{ \sum_{i=1}^\infty ip(1-p)^{i-1}=\frac{1}{p} }[/math]
Uniform({{{1}}}, {{{2}}})	[math]\displaystyle{ X\sim U(a,b) }[/math]	[math]\displaystyle{ \int_a^b \frac{x}{b-a}\,dx=\frac{a+b}{2} }[/math]
Exponential({{{1}}}, {{{2}}})	[math]\displaystyle{ X\sim \exp(\lambda) }[/math]	[math]\displaystyle{ \int_0^\infty \lambda xe^{-\lambda x}\,dx=\frac{1}{\lambda} }[/math]
Normal({{{1}}}, {{{2}}})	[math]\displaystyle{ X\sim N(\mu,\sigma^2) }[/math]	[math]\displaystyle{ \frac{1}{\sqrt{2\pi\sigma^2}}\int_{-\infty}^\infty xe^{-(x-\mu)^2/2\sigma^2}\,dx=\mu }[/math]
Standard Normal({{{1}}}, {{{2}}})	[math]\displaystyle{ X\sim N(0,1) }[/math]	[math]\displaystyle{ \frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty xe^{-x^2/2}\,dx=0 }[/math]
Pareto({{{1}}}, {{{2}}})	[math]\displaystyle{ X\sim \mathrm{Par}(\alpha, k) }[/math]	[math]\displaystyle{ \int_k^\infty\alpha k^\alpha x^{-\alpha}\,dx=\begin{cases}\frac{\alpha k}{\alpha-1}&\alpha\gt 1\\ \infty&0 \leq \alpha \leq 1.\end{cases} }[/math]
Cauchy({{{1}}}, {{{2}}})	[math]\displaystyle{ X\sim \mathrm{Cauchy}(x_0,\gamma) }[/math]	[math]\displaystyle{ \frac{1}{\pi}\int_{-\infty}^\infty \frac{\gamma x}{(x - x_0)^2 + \gamma^2}\,dx }[/math] is undefined

Properties

The basic properties below (and their names in bold) replicate or follow immediately from those of Lebesgue integral. Note that the letters "a.s." stand for "almost surely"—a central property of the Lebesgue integral. Basically, one says that an inequality like [math]\displaystyle{ X \geq 0 }[/math] is true almost surely, when the probability measure attributes zero-mass to the complementary event [math]\displaystyle{ \left\{ X \lt 0 \right\}. }[/math]

• Non-negativity: If [math]\displaystyle{ X \geq 0 }[/math] (a.s.), then [math]\displaystyle{ \operatorname{E}[ X] \geq 0. }[/math]

• Linearity of expectation: The expected value operator (or expectation operator) [math]\displaystyle{ \operatorname{E}[\cdot] }[/math] is linear in the sense that, for any random variables [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y, }[/math] and a constant [math]\displaystyle{ a, }[/math] [math]\displaystyle{ \begin{align} \operatorname{E}[X + Y] &= \operatorname{E}[X] + \operatorname{E}[Y], \\ \operatorname{E}[aX] &= a \operatorname{E}[X], \end{align} }[/math]

whenever the right-hand side is well-defined. By induction, this means that the expected value of the sum of any finite number of random variables is the sum of the expected values of the individual random variables, and the expected value scales linearly with a multiplicative constant. Symbolically, for [math]\displaystyle{ N }[/math] random variables [math]\displaystyle{ X_{i} }[/math] and constants [math]\displaystyle{ a_{i} (1\leq i \leq N), }[/math] we have [math]\displaystyle{ \operatorname{E}\left[\sum_{i=1}^{N}a_{i}X_{i}\right] = \sum_{i=1}^{N}a_{i}\operatorname{E}[X_{i}]. }[/math] If we think of the set of random variables with finite expected value as forming a vector space, then the linearity of expectation implies that the expected value is a linear form on this vector space.

• Monotonicity: If [math]\displaystyle{ X\leq Y }[/math] (a.s.), and both [math]\displaystyle{ \operatorname{E}[X] }[/math] and [math]\displaystyle{ \operatorname{E}[Y] }[/math] exist, then [math]\displaystyle{ \operatorname{E}[X]\leq\operatorname{E}[Y]. }[/math]
  Proof follows from the linearity and the non-negativity property for [math]\displaystyle{ Z=Y-X, }[/math] since [math]\displaystyle{ Z\geq 0 }[/math] (a.s.).
• Non-degeneracy: If [math]\displaystyle{ \operatorname{E}[|X|]=0, }[/math] then [math]\displaystyle{ X=0 }[/math] (a.s.).
• If [math]\displaystyle{ X = Y }[/math] (a.s.), then [math]\displaystyle{ \operatorname{E}[ X] = \operatorname{E}[ Y]. }[/math] In other words, if X and Y are random variables that take different values with probability zero, then the expectation of X will equal the expectation of Y.
• If [math]\displaystyle{ X=c }[/math] (a.s.) for some real number c, then [math]\displaystyle{ \operatorname{E}[X] = c. }[/math] In particular, for a random variable [math]\displaystyle{ X }[/math] with well-defined expectation, [math]\displaystyle{ \operatorname{E}[\operatorname{E}[X]] = \operatorname{E}[X]. }[/math] A well defined expectation implies that there is one number, or rather, one constant that defines the expected value. Thus follows that the expectation of this constant is just the original expected value.
• As a consequence of the formula |X| = X ⁺ + X ⁻ as discussed above, together with the triangle inequality, it follows that for any random variable [math]\displaystyle{ X }[/math] with well-defined expectation, one has [math]\displaystyle{ |\operatorname{E}[X]| \leq \operatorname{E}|X|. }[/math]
• Let 1_A denote the indicator function of an event A, then E[1_A] is given by the probability of A. This is nothing but a different way of stating the expectation of a Bernoulli random variable, as calculated in the table above.
• Formulas in terms of CDF: If [math]\displaystyle{ F(x) }[/math] is the cumulative distribution function of a random variable X, then

[math]\displaystyle{ \operatorname{E}[X] = \int_{-\infty}^\infty x\,dF(x), }[/math]

where the values on both sides are well defined or not well defined simultaneously, and the integral is taken in the sense of Lebesgue-Stieltjes. As a consequence of integration by parts as applied to this representation of E[X], it can be proved that [math]\displaystyle{ \operatorname{E}[X] = \int_0^\infty (1-F(x))\,dx - \int^0_{-\infty} F(x)\,dx, }[/math] with the integrals taken in the sense of Lebesgue.({{{1}}}, {{{2}}}) As a special case, for any random variable X valued in the nonnegative integers {0, 1, 2, 3, ...}, one has [math]\displaystyle{ \operatorname{E}[X]=\sum _{n=0}^\infty \operatorname{P}(X\gt n), }[/math]

where P denotes the underlying probability measure.

• Non-multiplicativity: In general, the expected value is not multiplicative, i.e. [math]\displaystyle{ \operatorname{E}[XY] }[/math] is not necessarily equal to [math]\displaystyle{ \operatorname{E}[X]\cdot \operatorname{E}[Y]. }[/math] If [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] are independent, then one can show that [math]\displaystyle{ \operatorname{E}[XY]=\operatorname{E}[X] \operatorname{E}[Y]. }[/math] If the random variables are dependent, then generally [math]\displaystyle{ \operatorname{E}[XY] \neq \operatorname{E}[X] \operatorname{E}[Y], }[/math] although in special cases of dependency the equality may hold.
• Law of the unconscious statistician: The expected value of a measurable function of [math]\displaystyle{ X, }[/math] [math]\displaystyle{ g(X), }[/math] given that [math]\displaystyle{ X }[/math] has a probability density function [math]\displaystyle{ f(x), }[/math] is given by the inner product of [math]\displaystyle{ f }[/math] and [math]\displaystyle{ g }[/math]: [math]\displaystyle{ \operatorname{E}[g(X)] = \int_{\R} g(x) f(x)\, dx . }[/math] This formula also holds in multidimensional case, when [math]\displaystyle{ g }[/math] is a function of several random variables, and [math]\displaystyle{ f }[/math] is their joint density.({{{1}}}, {{{2}}})

Inequalities

Concentration inequalities control the likelihood of a random variable taking on large values. Markov's inequality is among the best-known and simplest to prove: for a nonnegative random variable X and any positive number a, it states that({{{1}}}, {{{2}}}) [math]\displaystyle{ \operatorname{P}(X\geq a)\leq\frac{\operatorname{E}[X]}{a}. }[/math]

If X is any random variable with finite expectation, then Markov's inequality may be applied to the random variable |X−E[X]|² to obtain Chebyshev's inequality [math]\displaystyle{ \operatorname{P}(|X-\text{E}[X]|\geq a)\leq\frac{\operatorname{Var}[X]}{a^2}, }[/math] where Var is the variance.({{{1}}}, {{{2}}}) These inequalities are significant for their nearly complete lack of conditional assumptions. For example, for any random variable with finite expectation, the Chebyshev inequality implies that there is at least a 75% probability of an outcome being within two standard deviations of the expected value. However, in special cases the Markov and Chebyshev inequalities often give much weaker information than is otherwise available. For example, in the case of an unweighted dice, Chebyshev's inequality says that odds of rolling between 1 and 6 is at least 53%; in reality, the odds are of course 100%.({{{1}}}, {{{2}}}) The Kolmogorov inequality extends the Chebyshev inequality to the context of sums of random variables.({{{1}}}, {{{2}}})

The following three inequalities are of fundamental importance in the field of mathematical analysis and its applications to probability theory.

• Jensen's inequality: Let f: ℝ → ℝ be a convex function and X a random variable with finite expectation. Then({{{1}}}, {{{2}}}) [math]\displaystyle{ f(\operatorname{E}(X)) \leq \operatorname{E} (f(X)). }[/math]

Part of the assertion is that the negative part of f(X) has finite expectation, so that the right-hand side is well-defined (possibly infinite). Convexity of f can be phrased as saying that the output of the weighted average of two inputs under-estimates the same weighted average of the two outputs; Jensen's inequality extends this to the setting of completely general weighted averages, as represented by the expectation. In the special case that f(x) = |x|^t/s for positive numbers s < t, one obtains the Lyapunov inequality({{{1}}}, {{{2}}}) [math]\displaystyle{ \left(\operatorname{E}|X|^s\right)^{1/s}\leq\left(\operatorname{E}|X|^t\right)^{1/t}. }[/math]

This can also be proved by the Hölder inequality.({{{1}}}, {{{2}}}) In measure theory, this is particularly notable for proving the inclusion L^s ⊂ L^t of L^p spaces, in the special case of probability spaces.

• Hölder's inequality: if p > 1 and q > 1 are numbers satisfying p ⁻¹ + q ⁻¹ = 1, then [math]\displaystyle{ \operatorname{E}|XY|\leq(\operatorname{E}|X|^p)^{1/p}(\operatorname{E}|Y|^q)^{1/q}. }[/math]

for any random variables X and Y.({{{1}}}, {{{2}}}) The special case of p = q = 2 is called the Cauchy–Schwarz inequality, and is particularly well-known.({{{1}}}, {{{2}}})

• Minkowski inequality: given any number p ≥ 1, for any random variables X and Y with E|X|^p and E|Y|^p both finite, it follows that E|X + Y|^p is also finite and({{{1}}}, {{{2}}}) [math]\displaystyle{ \Bigl(\operatorname{E}|X+Y|^p\Bigr)^{1/p}\leq\Bigl(\operatorname{E}|X|^p\Bigr)^{1/p}+\Bigl(\operatorname{E}|Y|^p\Bigr)^{1/p}. }[/math]

The Hölder and Minkowski inequalities can be extended to general measure spaces, and are often given in that context. By contrast, the Jensen inequality is special to the case of probability spaces.

Expectations under convergence of random variables

In general, it is not the case that [math]\displaystyle{ \operatorname{E}[X_n] \to \operatorname{E}[X] }[/math] even if [math]\displaystyle{ X_n\to X }[/math] pointwise. Thus, one cannot interchange limits and expectation, without additional conditions on the random variables. To see this, let [math]\displaystyle{ U }[/math] be a random variable distributed uniformly on [math]\displaystyle{ [0,1]. }[/math] For [math]\displaystyle{ n\geq 1, }[/math] define a sequence of random variables

[math]\displaystyle{ X_n = n \cdot \mathbf{1}\left\{ U \in \left(0,\tfrac{1}{n}\right)\right\}, }[/math]

with [math]\displaystyle{ {\mathbf 1}\{A\} }[/math] being the indicator function of the event [math]\displaystyle{ A. }[/math] Then, it follows that [math]\displaystyle{ X_n \to 0 }[/math] pointwise. But, [math]\displaystyle{ \operatorname{E}[X_n] = n \cdot \operatorname{P}\left(U \in \left[ 0, \tfrac{1}{n}\right] \right) = n \cdot \tfrac{1}{n} = 1 }[/math] for each [math]\displaystyle{ n. }[/math] Hence, [math]\displaystyle{ \lim_{n \to \infty} \operatorname{E}[X_n] = 1 \neq 0 = \operatorname{E}\left[ \lim_{n \to \infty} X_n \right]. }[/math]

Analogously, for general sequence of random variables [math]\displaystyle{ \{ Y_n : n \geq 0\}, }[/math] the expected value operator is not [math]\displaystyle{ \sigma }[/math]-additive, i.e.

[math]\displaystyle{ \operatorname{E}\left[\sum^\infty_{n=0} Y_n\right] \neq \sum^\infty_{n=0}\operatorname{E}[Y_n]. }[/math]

An example is easily obtained by setting [math]\displaystyle{ Y_0 = X_1 }[/math] and [math]\displaystyle{ Y_n = X_{n+1} - X_n }[/math] for [math]\displaystyle{ n \geq 1, }[/math] where [math]\displaystyle{ X_n }[/math] is as in the previous example.

A number of convergence results specify exact conditions which allow one to interchange limits and expectations, as specified below.

• Monotone convergence theorem: Let [math]\displaystyle{ \{X_n : n \geq 0\} }[/math] be a sequence of random variables, with [math]\displaystyle{ 0 \leq X_n \leq X_{n+1} }[/math] (a.s) for each [math]\displaystyle{ n \geq 0. }[/math] Furthermore, let [math]\displaystyle{ X_n \to X }[/math] pointwise. Then, the monotone convergence theorem states that [math]\displaystyle{ \lim_n\operatorname{E}[X_n]=\operatorname{E}[X]. }[/math]
  Using the monotone convergence theorem, one can show that expectation indeed satisfies countable additivity for non-negative random variables. In particular, let [math]\displaystyle{ \{X_i\}^\infty_{i=0} }[/math] be non-negative random variables. It follows from monotone convergence theorem that [math]\displaystyle{ \operatorname{E}\left[\sum^\infty_{i=0}X_i\right] = \sum^\infty_{i=0}\operatorname{E}[X_i]. }[/math]
• Fatou's lemma: Let [math]\displaystyle{ \{ X_n \geq 0 : n \geq 0\} }[/math] be a sequence of non-negative random variables. Fatou's lemma states that [math]\displaystyle{ \operatorname{E}[\liminf_n X_n] \leq \liminf_n \operatorname{E}[X_n]. }[/math]
  Corollary. Let [math]\displaystyle{ X_n \geq 0 }[/math] with [math]\displaystyle{ \operatorname{E}[X_n] \leq C }[/math] for all [math]\displaystyle{ n \geq 0. }[/math] If [math]\displaystyle{ X_n \to X }[/math] (a.s), then [math]\displaystyle{ \operatorname{E}[X] \leq C. }[/math]
  Proof is by observing that [math]\displaystyle{ X = \liminf_n X_n }[/math] (a.s.) and applying Fatou's lemma.
• Dominated convergence theorem: Let [math]\displaystyle{ \{X_n : n \geq 0 \} }[/math] be a sequence of random variables. If [math]\displaystyle{ X_n\to X }[/math] pointwise (a.s.), [math]\displaystyle{ |X_n|\leq Y \leq +\infty }[/math] (a.s.), and [math]\displaystyle{ \operatorname{E}[Y]\lt \infty. }[/math] Then, according to the dominated convergence theorem,
  • [math]\displaystyle{ \operatorname{E}|X| \leq \operatorname{E}[Y] \lt \infty }[/math];
  • [math]\displaystyle{ \lim_n\operatorname{E}[X_n]=\operatorname{E}[X] }[/math]
  • [math]\displaystyle{ \lim_n\operatorname{E}|X_n - X| = 0. }[/math]
• Uniform integrability: In some cases, the equality [math]\displaystyle{ \lim_n\operatorname{E}[X_n]=\operatorname{E}[\lim_n X_n] }[/math] holds when the sequence [math]\displaystyle{ \{X_n\} }[/math] is uniformly integrable.

Relationship with characteristic function

The probability density function [math]\displaystyle{ f_X }[/math] of a scalar random variable [math]\displaystyle{ X }[/math] is related to its characteristic function [math]\displaystyle{ \varphi_X }[/math] by the inversion formula:

[math]\displaystyle{ f_X(x) = \frac{1}{2\pi}\int_{\mathbb{R}} e^{-itx}\varphi_X(t) \, \mathrm{d}t. }[/math]

For the expected value of [math]\displaystyle{ g(X) }[/math] (where [math]\displaystyle{ g:{\mathbb R}\to{\mathbb R} }[/math] is a Borel function), we can use this inversion formula to obtain

[math]\displaystyle{ \operatorname{E}[g(X)] = \frac{1}{2\pi} \int_{\mathbb R} g(x)\left[ \int_{\mathbb R} e^{-itx}\varphi_X(t) \, \mathrm{d}t \right]\,\mathrm{d}x. }[/math]

If [math]\displaystyle{ \operatorname{E}[g(X)] }[/math] is finite, changing the order of integration, we get, in accordance with Fubini–Tonelli theorem,

[math]\displaystyle{ \operatorname{E}[g(X)] = \frac{1}{2\pi} \int_{\mathbb R} G(t) \varphi_X(t) \, \mathrm{d}t, }[/math]

where

[math]\displaystyle{ G(t) = \int_{\mathbb R} g(x) e^{-itx} \, \mathrm{d}x }[/math]

is the Fourier transform of [math]\displaystyle{ g(x). }[/math] The expression for [math]\displaystyle{ \operatorname{E}[g(X)] }[/math] also follows directly from the Plancherel theorem.

Uses and applications

The expectation of a random variable plays an important role in a variety of contexts.

In statistics, where one seeks estimates for unknown parameters based on available data gained from samples, the sample mean serves as an estimate for the expectation, and is itself a random variable. In such settings, the sample mean is considered to meet the desirable criterion for a "good" estimator in being unbiased; that is, the expected value of the estimate is equal to the true value of the underlying parameter.

For a different example, in decision theory, an agent making an optimal choice in the context of incomplete information is often assumed to maximize the expected value of their utility function.

It is possible to construct an expected value equal to the probability of an event by taking the expectation of an indicator function that is one if the event has occurred and zero otherwise. This relationship can be used to translate properties of expected values into properties of probabilities, e.g. using the law of large numbers to justify estimating probabilities by frequencies.

The expected values of the powers of X are called the moments of X; the moments about the mean of X are expected values of powers of X − E[X]. The moments of some random variables can be used to specify their distributions, via their moment generating functions.

To empirically estimate the expected value of a random variable, one repeatedly measures observations of the variable and computes the arithmetic mean of the results. If the expected value exists, this procedure estimates the true expected value in an unbiased manner and has the property of minimizing the sum of the squares of the residuals (the sum of the squared differences between the observations and the estimate). The law of large numbers demonstrates (under fairly mild conditions) that, as the size of the sample gets larger, the variance of this estimate gets smaller.

This property is often exploited in a wide variety of applications, including general problems of statistical estimation and machine learning, to estimate (probabilistic) quantities of interest via Monte Carlo methods, since most quantities of interest can be written in terms of expectation, e.g. [math]\displaystyle{ \operatorname{P}({X \in \mathcal{A}}) = \operatorname{E}[{\mathbf 1}_{\mathcal{A}}], }[/math] where [math]\displaystyle{ {\mathbf 1}_{\mathcal{A}} }[/math] is the indicator function of the set [math]\displaystyle{ \mathcal{A}. }[/math]

The mass of probability distribution is balanced at the expected value, here a Beta(α,β) distribution with expected value α/(α+β).

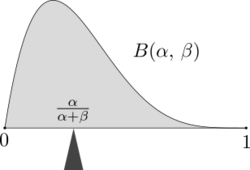
In classical mechanics, the center of mass is an analogous concept to expectation. For example, suppose X is a discrete random variable with values x_i and corresponding probabilities p_i. Now consider a weightless rod on which are placed weights, at locations x_i along the rod and having masses p_i (whose sum is one). The point at which the rod balances is E[X].

Expected values can also be used to compute the variance, by means of the computational formula for the variance

[math]\displaystyle{ \operatorname{Var}(X)= \operatorname{E}[X^2] - (\operatorname{E}[X])^2. }[/math]

A very important application of the expectation value is in the field of quantum mechanics. The expectation value of a quantum mechanical operator [math]\displaystyle{ \hat{A} }[/math] operating on a quantum state vector [math]\displaystyle{ |\psi\rangle }[/math] is written as [math]\displaystyle{ \langle\hat{A}\rangle = \langle\psi|A|\psi\rangle. }[/math] The uncertainty in [math]\displaystyle{ \hat{A} }[/math] can be calculated by the formula [math]\displaystyle{ (\Delta A)^2 = \langle\hat{A}^2\rangle - \langle \hat{A} \rangle^2 }[/math].

See also

• Central tendency
• Conditional expectation
• Expectation (epistemic)
• Law of total expectation – the expected value of the conditional expected value of X given Y is the same as the expected value of X
• Nonlinear expectation – a generalization of the expected value
• Population mean
• Predicted value
• Wald's equation – an equation for calculating the expected value of a random number of random variables

Bibliography

• Edwards, A.W.F (2002). Pascal's arithmetical triangle: the story of a mathematical idea (2nd ed.). JHU Press. ISBN 0-8018-6946-3. 
• Huygens, Christiaan (1657) (English translation, published in 1714). De ratiociniis in ludo aleæ. http://www.york.ac.uk/depts/maths/histstat/huygens.pdf. 
• Billingsley, Patrick (1995). Probability and measure. Wiley Series in Probability and Mathematical Statistics (Third edition of 1979 original ed.). New York: John Wiley & Sons, Inc.. ISBN 0-471-00710-2. 
• Casella, George; Berger, Roger L. (2001). Statistical inference. Duxbury Advanced Series (Second edition of 1990 original ed.). Pacific Grove, CA: Duxbury. ISBN 0-534-11958-1. 
• Feller, William (1968). An introduction to probability theory and its applications. Volume I (Third edition of 1950 original ed.). New York–London–Sydney: John Wiley & Sons, Inc.. 
• Feller, William (1971). An introduction to probability theory and its applications. Volume II (Second edition of 1966 original ed.). New York–London–Sydney: John Wiley & Sons, Inc.. 
• Johnson, Norman L.; Kotz, Samuel; Balakrishnan, N. (1994). Continuous univariate distributions. Volume 1. Wiley Series in Probability and Mathematical Statistics (Second edition of 1970 original ed.). New York: John Wiley & Sons, Inc.. ISBN 0-471-58495-9. 
• Papoulis, Athanasios; Pillai, S. Unnikrishna (2002). Probability, random variables, and stochastic processes (Fourth edition of 1965 original ed.). New York: McGraw-Hill. ISBN 0-07-366011-6.  (Erratum:  [1])
• Ross, Sheldon M. (2019). Introduction to probability models (Twelfth edition of 1972 original ed.). London: Academic Press. doi:10.1016/C2017-0-01324-1. ISBN 978-0-12-814346-9.