Conchoid (mathematics)

Short description: Curve traced by a line as it slides along another curve about a fixed point

Conchoids of line with common center.

  Fixed point O

  Given curve

Each pair of coloured curves is length d from the intersection with the line that a ray through O makes.

  d > distance of O from the line

  d = distance of O from the line

  d < distance of O from the line

Conchoid of Nicomedes drawn by an apparatus illustrated in Eutocius' Commentaries on the works of Archimedes

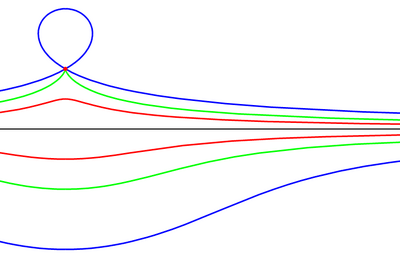
In geometry, a conchoid is a curve derived from a fixed point O, another curve, and a length d. It was invented by the ancient Greek mathematician Nicomedes.

Description

For every line through O that intersects the given curve at A the two points on the line which are d from A are on the conchoid. The conchoid is, therefore, the cissoid of the given curve and a circle of radius d and center O. They are called conchoids because the shape of their outer branches resembles conch shells.

The simplest expression uses polar coordinates with O at the origin. If

[math]\displaystyle{ r=\alpha(\theta) }[/math]

expresses the given curve, then

[math]\displaystyle{ r=\alpha(\theta)\pm d }[/math]

expresses the conchoid.

If the curve is a line, then the conchoid is the conchoid of Nicomedes.

For instance, if the curve is the line x = a, then the line's polar form is r = a sec θ and therefore the conchoid can be expressed parametrically as

[math]\displaystyle{ x=a \pm d \cos \theta,\, y=a \tan \theta \pm d \sin \theta. }[/math]

A limaçon is a conchoid with a circle as the given curve.

The so-called conchoid of de Sluze and conchoid of Dürer are not actually conchoids. The former is a strict cissoid and the latter a construction more general yet.

See also

• Cissoid
• Strophoid

References

• J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 36, 49–51, 113, 137. ISBN 0-486-60288-5. https://archive.org/details/catalogofspecial00lawr/page/36. 

External links

• conchoid with conic sections - interactive illustration
• Weisstein, Eric W.. "Conchoid of Nicomedes". http://mathworld.wolfram.com/ConchoidofNicomedes.html. 
• conchoid at mathcurves.com