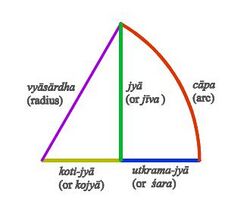
Jyā, koti-jyā and utkrama-jyā
Jyā, koṭi-jyā and utkrama-jyā are three trigonometric functions introduced by Indian mathematicians and astronomers. The earliest known Indian treatise containing references to these functions is Surya Siddhanta.[1] These are functions of arcs of circles and not functions of angles. Jyā and koti-jyā are closely related to the modern trigonometric functions of sine and cosine. In fact, the origins of the modern terms of "sine" and "cosine" have been traced back to the Sanskrit words jyā and koti-jyā.[1]
Definition
Let 'arc AB' denote an arc whose two extremities are A and B of a circle with center O. If a perpendicular BM be dropped from B to OA, then:
- jyā of arc AB = BM
- koti-jyā of arc AB = OM
- utkrama-jyā of arc AB = MA
If the radius of the circle is R and the length of arc AB is s, the angle subtended by arc AB at O measured in radians is θ = s / R. The three Indian functions are related to modern trigonometric functions as follows:
- jyā ( arc AB ) = R sin ( s / R )
- koti-jyā ( arc AB ) = R cos ( s / R )
- utkrama-jyā ( arc AB ) = R ( 1 - cos ( s / R ) ) = R versin ( s / R )
Terminology
An arc of a circle is like a bow and so is called a dhanu or chāpa which in Sanskrit means "a bow". The straight line joining the two extremities of an arc of a circle is like the string of a bow and this line is a chord of the circle. This chord is called a jyā which in Sanskrit means "a bow-string", presumably translating Hipparchus's χορδή with the same meaning[citation needed]. The word jīvá is also used as a synonym for jyā in geometrical literature.[2] At some point, Indian astronomers and mathematicians realised that computations would be more convenient if one used the halves of the chords instead of the full chords and associated the half-chords with the halves of the arcs.[1][3] The half-chords were called ardha-jyās or jyā-ardhas. These terms were again shortened to jyā by omitting the qualifier ardha which meant "half of".
The Sanskrit word koṭi has the meaning of "point, cusp", and specifically "the curved end of a bow". In trigonometry, it came to denote "the complement of an arc to 90°". Thus koṭi-jyā is "the jyā of the complementary arc". In Indian treatises, especially in commentaries, koṭi-jyā is often abbreviated as kojyā. The term koṭi also denotes "the side of a right angled triangle". Thus koṭi-jyā could also mean the other cathetus of a right triangle, the first cathetus being the jyā.[clarification needed][1]
Utkrama means "inverted", thus utkrama-jyā means "inverted chord". The tabular values of utkrama-jyā are derived from the tabular values of jyā by subtracting the elements from the radius in the reversed order.[clarification needed] This is really[clarification needed] the arrow between the bow and the bow-string and hence it has also been called bāṇa, iṣu or śara all meaning "arrow".[1]
An arc of a circle which subtends an angle of 90° at the center is called a vritta-pāda (a quadrat of a circle). Each zodiacal sign defines an arc of 30° and three consecutive zodiacal signs defines a vritta-pāda. The jyā of a vritta-pāda is the radius of the circle. The Indian astronomers coined the term tri-jyā to denote the radius of the base circle, the term tri-jyā being indicative of "the jyā of three signs". The radius is also called vyāsārdha, viṣkambhārdha, vistarārdha, etc., all meaning "semi-diameter".[1]
According to one convention, the functions jyā and koti-jyā are respectively denoted by "Rsin" and "Rcos" treated as single words.[1] Others denote jyā and koti-jyā respectively by "Sin" and "Cos" (the first letters being capital letters in contradistinction to the first letters being small letters in ordinary sine and cosine functions).[3]
From jyā to sine
The origins of the modern term sine have been traced to the Sanskrit word jyā,[4][5] or more specifically to its synonym jīvá. This term was adopted in medieval Islamic mathematics, transliterated in Arabic as Script error: The function "transl" does not exist. (جيب). Since Arabic is written without short vowels – and as a borrowing the long vowel is here denoted with yāʾ – this was interpreted as the homograph Script error: The function "transl" does not exist., Script error: The function "transl" does not exist. (جيب), which means "bosom". The text's 12th-century Latin translator used the Latin equivalent for "bosom", sinus.[6] When jyā became sinus, it has been suggested that by analogy kojyā became co-sinus. However, in early medieval texts, the cosine is called the complementi sinus "sine of the complement", suggesting the similarity to kojyā is coincidental.[7]
See also
References
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 B.B. Datta and A.N. Singh (1983). "Hindu Trigonometry". Indian Journal of History of Science 18 (1): 39–108. https://linux.ime.usp.br/~bedulli/Datta-Singh_hindu-trigonometry-1983.pdf. Retrieved 2 June 2022.
- ↑ According to lexicographers, it is a synonym also meaning "bow-string", but only its geometrical meaning is attested in literature. Monier-Williams, A Sanskrit Dictionary (1899): " jīvá n. (in geom. = jyā) the chord of an arc; the sine of an arc Suryasiddhanta 2.57"; jīvá as a generic adjective has the meaning of "living, alive" (cognate with English quick)
- ↑ 3.0 3.1 Glen Van Brummelen (2009). The mathematics of the heavens and the earth : the early history of trigonometry. Princeton University Press. pp. 95–97. ISBN 978-0-691-12973-0.
- ↑ "How the Trig Functions Got their Names". Ask Dr. Math. Drexel University. http://mathforum.org/library/drmath/view/54053.html.
- ↑ J J O'Connor and E F Robertson (June 1996). "The trigonometric functions". http://www-history.mcs.st-andrews.ac.uk/HistTopics/Trigonometric_functions.html.
- ↑ Various sources credit the first use of sinus to either:
- Plato Tiburtinus's 1116 translation of the Astronomy of Al-Battani
- Gerard of Cremona's c. 1150 translation of the Algebra of al-Khwārizmī
- Robert of Chester's 1145 translation of the tables of al-Khwārizmī
See Maor (1998), chapter 3, for an earlier etymology crediting Gerard.
See Katx, Victor (July 2008) (in en). A history of mathematics (3rd ed.). Boston: Pearson. p. 210 (sidebar). ISBN 978-0321387004. - ↑ "cosine". https://www.etymonline.com/word/cosine.
 |