METEOR

METEOR (Metric for Evaluation of Translation with Explicit ORdering) is a metric for the evaluation of machine translation output. The metric is based on the harmonic mean of unigram precision and recall, with recall weighted higher than precision. It also has several features that are not found in other metrics, such as stemming and synonymy matching, along with the standard exact word matching. The metric was designed to fix some of the problems found in the more popular BLEU metric, and also produce good correlation with human judgement at the sentence or segment level. This differs from the BLEU metric in that BLEU seeks correlation at the corpus level.

Example alignment (a).

Results have been presented which give correlation of up to 0.964 with human judgement at the corpus level, compared to BLEU's achievement of 0.817 on the same data set. At the sentence level, the maximum correlation with human judgement achieved was 0.403.

Example alignment (b).

Algorithm

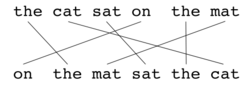
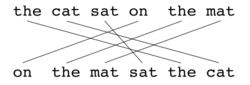
As with BLEU, the basic unit of evaluation is the sentence, the algorithm first creates an alignment (see illustrations) between two sentences, the candidate translation string, and the reference translation string. The alignment is a set of mappings between unigrams. A mapping can be thought of as a line between a unigram in one string, and a unigram in another string. The constraints are as follows; every unigram in the candidate translation must map to zero or one unigram in the reference. Mappings are selected to produce an alignment as defined above. If there are two alignments with the same number of mappings, the alignment is chosen with the fewest crosses, that is, with fewer intersections of two mappings. From the two alignments shown, alignment (a) would be selected at this point. Stages are run consecutively and each stage only adds to the alignment those unigrams which have not been matched in previous stages. Once the final alignment is computed, the score is computed as follows: Unigram precision P is calculated as:

Examples of pairs of words which will be mapped by each module

Module	Candidate	Reference	Match
Exact	Good	Good	Yes
Stemmer	Goods	Good	Yes
Synonymy	well	Good	Yes

[math]\displaystyle{ P = \frac{m}{w_{t}} }[/math]

Where m is the number of unigrams in the candidate translation that are also found in the reference translation, and [math]\displaystyle{ w_{t} }[/math] is the number of unigrams in the candidate translation. Unigram recall R is computed as:

[math]\displaystyle{ R = \frac{m}{w_{r}} }[/math]

Where m is as above, and [math]\displaystyle{ w_{r} }[/math] is the number of unigrams in the reference translation. Precision and recall are combined using the harmonic mean in the following fashion, with recall weighted 9 times more than precision:

[math]\displaystyle{ F_{mean} = \frac{10PR}{R+9P} }[/math]

The measures that have been introduced so far only account for congruity with respect to single words but not with respect to larger segments that appear in both the reference and the candidate sentence. In order to take these into account, longer n-gram matches are used to compute a penalty p for the alignment. The more mappings there are that are not adjacent in the reference and the candidate sentence, the higher the penalty will be.

In order to compute this penalty, unigrams are grouped into the fewest possible chunks, where a chunk is defined as a set of unigrams that are adjacent in the hypothesis and in the reference. The longer the adjacent mappings between the candidate and the reference, the fewer chunks there are. A translation that is identical to the reference will give just one chunk. The penalty p is computed as follows,

[math]\displaystyle{ p = 0.5 \left ( \frac{c}{u_{m}} \right )^3 }[/math]

Where c is the number of chunks, and [math]\displaystyle{ u_{m} }[/math] is the number of unigrams that have been mapped. The final score for a segment is calculated as M below. The penalty has the effect of reducing the [math]\displaystyle{ F_{mean} }[/math] by up to 50% if there are no bigram or longer matches.

[math]\displaystyle{ M = F_{mean} (1 - p) }[/math]

To calculate a score over a whole corpus, or collection of segments, the aggregate values for P, R and p are taken and then combined using the same formula. The algorithm also works for comparing a candidate translation against more than one reference translations. In this case the algorithm compares the candidate against each of the references and selects the highest score.

Examples

Reference	the	cat	sat	on	the	mat
Hypothesis	on	the	mat	sat	the	cat
Score	[math]\displaystyle{ 0.9375 = \underset\text{Fmean}{1.0000} \times (1 - \underset\text{Penalty}{0.0625}) }[/math]
Fmean	[math]\displaystyle{ 1.0000 = 10 \times \underset\text{Precision}{1.0000} \times \frac\overset\text{Recall}{1.0000}{\underset\text{Recall}{1.0000} + 9 \times \underset\text{Precision}{1.0000}} }[/math]
Penalty	[math]\displaystyle{ 0.0625 = 0.5 \times \underset\text{Fragmentation}{0.5^3} }[/math]
Fragmentation	[math]\displaystyle{ 0.5 = \frac\overset\text{Chunks}{3.0000}\underset\text{Matches}{6.0000} }[/math]

Reference	the	cat	sat	on	the	mat
Hypothesis	the	cat	sat	on	the	mat
Score	[math]\displaystyle{ 0.9977 = \underset\text{Fmean}{1.0000} \times (1 - \underset\text{Penalty}{0.0023}) }[/math]
Fmean	[math]\displaystyle{ 1.0000 = 10 \times \underset\text{Precision}{1.0000} \times \frac\overset\text{Recall}{1.0000}{\underset\text{Recall}{1.0000} + 9 \times \underset\text{Precision}{1.0000}} }[/math]
Penalty	[math]\displaystyle{ 0.0023 = 0.5 \times \underset\text{Fragmentation}{0.1667^3} }[/math]
Fragmentation	[math]\displaystyle{ 0.1667 = \frac\overset\text{Chunks}{1.0000}\underset\text{Matches}{6.0000} }[/math]

Reference	the	cat		sat	on	the	mat
Hypothesis	the	cat	was	sat	on	the	mat
Score	[math]\displaystyle{ 0.9654 = \underset\text{Fmean}{0.9836} \times (1 - \underset\text{Penalty}{0.0185}) }[/math]
Fmean	[math]\displaystyle{ 0.9836 = 10 \times \underset\text{Precision}{0.8571} \times \frac{\overset\text{Recall}{1.0000}}{\underset\text{Recall}{1.0000} + 9 \times \underset\text{Precision}{0.8571}} }[/math]
Penalty	[math]\displaystyle{ 0.0185 = 0.5 \times \underset\text{Fragmentation}{0.3333^3} }[/math]
Fragmentation	[math]\displaystyle{ 0.3333 = \frac\overset\text{Chunks}{2.0000}\underset\text{Matches}{6.0000} }[/math]

See also

• BLEU
• F-Measure
• NIST (metric)
• ROUGE (metric)
• Word Error Rate (WER)
• LEPOR
• Noun-Phrase Chunking

Notes

1. ^ Banerjee, S. and Lavie, A. (2005)

References

• Banerjee, S. and Lavie, A. (2005) "METEOR: An Automatic Metric for MT Evaluation with Improved Correlation with Human Judgments" in Proceedings of Workshop on Intrinsic and Extrinsic Evaluation Measures for MT and/or Summarization at the 43rd Annual Meeting of the Association of Computational Linguistics (ACL-2005), Ann Arbor, Michigan, June 2005
• Lavie, A., Sagae, K. and Jayaraman, S. (2004) "The Significance of Recall in Automatic Metrics for MT Evaluation" in Proceedings of AMTA 2004, Washington DC. September 2004

External links

• The METEOR Automatic Machine Translation Evaluation System (including link for download)