Metric (mathematics)

From HandWiki
Short description: Mathematical function defining distance
An illustration comparing the taxicab metric to the Euclidean metric on the plane: According to the taxicab metric the red, yellow, and blue paths have the same length (12). According to the Euclidean metric, the green path has length [math]\displaystyle{ 6 \sqrt{2} \approx 8.49 }[/math], and is the unique shortest path.

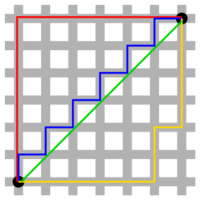
In mathematics, a metric or distance function is a function that gives a distance between each pair of point elements of a set. A set with a metric is a metric space.[1] A metric induces a topology on a set, but not all topologies can be generated by a metric. A topological space whose topology can be described by a metric is a metrizable space.

One important source of metrics in differential geometry are metric tensors, bilinear forms that may be defined from the tangent vectors of a differentiable manifold onto a scalar. A metric tensor allows distances along curves to be determined through integration, and thus determines a metric.

Definition

A metric on a set X is a function (called distance function or simply distance)

[math]\displaystyle{ d : X \times X \to \R, }[/math]

such that for all [math]\displaystyle{ x, y, z \in X }[/math], the following three axioms hold:

1. [math]\displaystyle{ d(x, y) = 0 \iff x = y }[/math] identity of indiscernibles
2. [math]\displaystyle{ d(x, y) = d(y, x) }[/math] symmetry
3. [math]\displaystyle{ d(x, z) \leq d(x, y) + d(y, z) }[/math] triangle inequality

From these axioms the non-negativity of metrics can be derived like so:

[math]\displaystyle{ d(x,y) + d(y,x) \ge d(x,x) }[/math] by triangle inequality
[math]\displaystyle{ d(x,y) + d(x,y) \ge d(x,x) }[/math] by symmetry
[math]\displaystyle{ 2d(x,y) \ge 0 }[/math] by identity of indiscernibles
4. [math]\displaystyle{ d(x,y) \ge 0 }[/math] we have non-negativity

A metric (as defined) is a non-negative real-valued function. This, together with axiom 1, provides a separation condition, where distinct or separate points are precisely those that have a positive distance between them.

A metric is called an ultrametric if it satisfies the following stronger version of the triangle inequality for all [math]\displaystyle{ x,y,z\in X }[/math]:

[math]\displaystyle{ d(x, y) \leq \max \{ d(x, z), d(y, z) \}. }[/math]

A metric [math]\displaystyle{ d }[/math] on [math]\displaystyle{ X }[/math] is called intrinsic if for all [math]\displaystyle{ x, y\in X }[/math] and any length [math]\displaystyle{ L \gt d(x,y) }[/math], there exists a curve of length less than [math]\displaystyle{ L }[/math] that joins [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math].

A metric [math]\displaystyle{ d }[/math] on a group [math]\displaystyle{ G }[/math] (written multiplicatively) is said to be left-invariant (resp. right-invariant) if for all [math]\displaystyle{ x, y, z \in G }[/math]

[math]\displaystyle{ d(zx, zy) = d(x, y) }[/math] [resp. [math]\displaystyle{ d(xz,yz)=d(x,y) }[/math]].

A metric [math]\displaystyle{ d }[/math] on a commutative additive group [math]\displaystyle{ X }[/math] is said to be translation invariant if for all [math]\displaystyle{ x,y,z\in X }[/math]

[math]\displaystyle{ d(x, y) = d(x + z, y + z), }[/math]or equivalently [math]\displaystyle{ d(x, y) = d(x - y, 0). }[/math]

Every vector space is also a commutative additive group and a metric on a real or complex vector space that is induced by a norm is always translation invariant. A metric [math]\displaystyle{ d }[/math] on a real or complex vector space [math]\displaystyle{ V }[/math] is induced by a norm if and only if it is translation invariant and absolutely homogeneous, where the latter means that for all scalars [math]\displaystyle{ s }[/math] and all [math]\displaystyle{ x, y \in V }[/math]: [math]\displaystyle{ d(sx, sy) = |s| d(x, y) }[/math] holds, in which case the function [math]\displaystyle{ {\|x\|} := d(x, 0) }[/math] defines a norm on [math]\displaystyle{ V }[/math] and the canonical metric induced by [math]\displaystyle{ \| \cdot \| }[/math] is equal to [math]\displaystyle{ d. }[/math]

Notes

These conditions express intuitive notions about the concept of distance. For example, that the distance between distinct points is positive and the distance from x to y is the same as the distance from y to x. The triangle inequality means that the distance from x to z via y is at least as great as from x to z directly. Euclid in his work stated that the shortest distance between two points is a line; that was the triangle inequality for his geometry.

Examples

  • The discrete metric: [math]\displaystyle{ d(x,y)=\begin{cases}0 & \text{if }x=y,\\ 1 & \text{otherwise.}\end{cases} }[/math]
  • The Euclidean metric is translation and rotation invariant.
  • The taxicab metric is translation invariant.
  • More generally, any metric induced by a norm is translation invariant.
  • If [math]\displaystyle{ (p_n)_{n\in \N} }[/math] is a sequence of seminorms defining a (locally convex) topological vector space E, then
    [math]\displaystyle{ d(x,y)=\sum_{n=1}^\infty \frac{1}{2^n} \frac{p_n(x-y)}{1+p_n(x-y)} }[/math]
    is a metric defining the same topology. (One can replace [math]\displaystyle{ \frac{1}{2^n} }[/math] by any summable sequence [math]\displaystyle{ (a_n) }[/math] of strictly positive numbers.)
  • The normed space [math]\displaystyle{ (\R, {|\cdot |}) }[/math] is a Banach space where the absolute value is a norm on the real line [math]\displaystyle{ \R }[/math] that induces the usual Euclidean topology on [math]\displaystyle{ \R. }[/math] Define a metric [math]\displaystyle{ d : \R \times \R \to \R }[/math] on [math]\displaystyle{ \R }[/math] by [math]\displaystyle{ d(x, y) = {|\arctan(x) - \arctan(y)|} }[/math] for all [math]\displaystyle{ x,y\in\R. }[/math] Just like [math]\displaystyle{ {|\cdot |} }[/math] 's induced metric, the metric [math]\displaystyle{ d }[/math] also induces the usual Euclidean topology on [math]\displaystyle{ \R }[/math]. However, [math]\displaystyle{ d }[/math] is not a complete metric because the sequence [math]\displaystyle{ x_{\bull} = \left(x_i\right)_{i=1}^{\infty} }[/math] defined by [math]\displaystyle{ x_i := i }[/math] is a [math]\displaystyle{ d }[/math]‑Cauchy sequence but it does not converge to any point of [math]\displaystyle{ \R }[/math]. As a consequence of not converging, this [math]\displaystyle{ d }[/math]-Cauchy sequence cannot be a Cauchy sequence in [math]\displaystyle{ (\R, {|\cdot |}) }[/math] (i.e. it is not a Cauchy sequence with respect to the norm [math]\displaystyle{ {\|\cdot \|} }[/math]) because if it was [math]\displaystyle{ | \cdot | }[/math]-Cauchy, then the fact that [math]\displaystyle{ (\R, {|\cdot |}) }[/math] is a Banach space would imply that it converges (a contradiction).[2]
  • Graph metric, a metric defined in terms of distances in a certain graph.
  • The Hamming distance in coding theory.
  • Riemannian metric, a type of metric function that is appropriate to impose on any differentiable manifold. For any such manifold, one chooses at each point p a symmetric, positive definite, bilinear form [math]\displaystyle{ L: \mathrm{T}_p\times\mathrm{ T}_p\to\R }[/math] on the tangent space [math]\displaystyle{ \mathrm{T}_p }[/math] at [math]\displaystyle{ p }[/math], doing so in a smooth manner. This form determines the length of any tangent vector [math]\displaystyle{ \mathbf v }[/math] on the manifold, via the definition [math]\displaystyle{ {\|v\|} = \sqrt{L(\mathbf{v}, \mathbf{v})} }[/math]. Then for any differentiable path on the manifold, its length is defined as the integral of the length of the tangent vector to the path at any point, where the integration is done with respect to the path parameter. Finally, to get a metric defined on any pair [math]\displaystyle{ \{x,y\} }[/math] of points of the manifold, one takes the infimum, over all paths from [math]\displaystyle{ x }[/math] to [math]\displaystyle{ y, }[/math]of the set of path lengths. A smooth manifold equipped with a Riemannian metric is called a Riemannian manifold.
  • The Fubini–Study metric on complex projective space. This is an example of a Riemannian metric.
  • String metrics, such as Levenshtein distance and other string edit distances, define a metric over strings.
  • Graph edit distance defines a distance function between graphs.
  • The Wasserstein metric is a distance function defined between two probability distributions.
  • The Finsler metric is a continuous nonnegative function [math]\displaystyle{ F: \mathrm{TM}\to [0,\infty) }[/math] defined on the tangent bundle.

Equivalence of metrics

For a given set X, two metrics [math]\displaystyle{ d_1 }[/math] and [math]\displaystyle{ d_2 }[/math] are called topologically equivalent (uniformly equivalent) if the identity mapping

[math]\displaystyle{ {\rm id}: (X,d_1)\to (X,d_2) }[/math]

is a homeomorphism (uniform isomorphism).

For example, if [math]\displaystyle{ d }[/math] is a metric, then [math]\displaystyle{ \min (d, 1) }[/math] and [math]\displaystyle{ \frac{d}{1+d} }[/math] are metrics equivalent to [math]\displaystyle{ d. }[/math]


Norm induced metric

Norms on vector spaces are equivalent to certain metrics, namely homogeneous, translation-invariant ones. In other words, every norm determines a metric, and some metrics determine a norm.

Given a normed vector space [math]\displaystyle{ (X, {\|\cdot\|}) }[/math] we can define a metric [math]\displaystyle{ d }[/math] on [math]\displaystyle{ X, }[/math] called the metric induced by [math]\displaystyle{ \| \cdot \| }[/math] or simply the norm induced metric, by

[math]\displaystyle{ d(x,y) := {\| x-y\|}. }[/math]

The metric [math]\displaystyle{ d }[/math] is said to be induced by the norm [math]\displaystyle{ {\|\cdot\|}. }[/math]

Conversely[3] if a metric [math]\displaystyle{ d }[/math] on a vector space [math]\displaystyle{ X }[/math] satisfies the properties

  • Translation invariance: [math]\displaystyle{ d(x,y) = d(x+a,y+a) }[/math];
  • Absolute homogeneity: [math]\displaystyle{ d(\alpha x, \alpha y) = |\alpha| d(x,y) }[/math];

then a norm on [math]\displaystyle{ X }[/math] may be defined by

[math]\displaystyle{ {\|x\|} := d(x,0) }[/math]

where the metric induced by this norm is the original given metric [math]\displaystyle{ d. }[/math]

Similarly, a seminorm induces a pseudometric (see below), and a homogeneous, translation invariant pseudometric induces a seminorm.

Metrics on multisets

We can generalize the notion of a metric from a distance between two elements to a distance between two nonempty finite multisets of elements. A multiset is a generalization of the notion of a set such that an element can occur more than once. Define the multiset union [math]\displaystyle{ U=XY }[/math] if [math]\displaystyle{ U }[/math] is the multiset consisting of the elements of the multisets [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math], that is, if [math]\displaystyle{ x }[/math] occurs [math]\displaystyle{ m }[/math] times in [math]\displaystyle{ X }[/math] and [math]\displaystyle{ n }[/math] times in [math]\displaystyle{ Y }[/math] then it occurs [math]\displaystyle{ m+n }[/math] times in [math]\displaystyle{ U }[/math]. A distance function [math]\displaystyle{ d }[/math] on the set of nonempty finite multisets is a metric[4] if

  1. [math]\displaystyle{ d(X)=0 }[/math] if all elements of [math]\displaystyle{ X }[/math] are equal and [math]\displaystyle{ d(X) \gt 0 }[/math] otherwise (positive definiteness), that is, (non-negativity plus identity of indiscernibles)
  2. [math]\displaystyle{ d(X) }[/math] is invariant under all permutations of [math]\displaystyle{ X }[/math] (symmetry)
  3. [math]\displaystyle{ d(XY) \leq d(XZ)+d(ZY) }[/math] (triangle inequality)

Note that the familiar metric between two elements results if the multiset [math]\displaystyle{ X }[/math] has two elements in 1 and 2 and the multisets [math]\displaystyle{ X,Y,Z }[/math] have one element each in 3. For instance if [math]\displaystyle{ X }[/math] consists of two occurrences of [math]\displaystyle{ x }[/math], then [math]\displaystyle{ d(X)=0 }[/math] according to 1.

A simple example is the set of all nonempty finite multisets [math]\displaystyle{ X }[/math] of integers with [math]\displaystyle{ d(X)=\max (X)- \min (X) }[/math]. More complex examples are information distance in multisets;[4] and normalized compression distance (NCD) in multisets.[5]

Generalized metrics

There are numerous ways of relaxing the axioms of metrics, giving rise to various notions of generalized metric spaces. These generalizations can also be combined. The terminology used to describe them is not completely standardized. Most notably, in functional analysis pseudometrics often come from seminorms on vector spaces, and so it is natural to call them "semimetrics". This conflicts with the use of the term in topology.

Extended metrics

Some authors allow the distance function d to attain the value ∞, i.e. distances are non-negative numbers on the extended real number line. Such a function is called an extended metric or "∞-metric". Every extended metric can be transformed to a finite metric such that the metric spaces are equivalent as far as notions of topology (such as continuity or convergence) are concerned. This can be done using a subadditive monotonically increasing bounded function which is zero at zero, e.g. [math]\displaystyle{ d'(x, y) = d(x, y) / (1 + d(x, y)) }[/math] or [math]\displaystyle{ d''(x, y) = \min(1, d(x, y)) }[/math].

The requirement that the metric take values in [math]\displaystyle{ [0,\infty) }[/math] can even be relaxed to consider metrics with values in other directed sets. The reformulation of the axioms in this case leads to the construction of uniform spaces: topological spaces with an abstract structure enabling one to compare the local topologies of different points.

Pseudometrics

Main page: Pseudometric space

A pseudometric on [math]\displaystyle{ X }[/math] is a function [math]\displaystyle{ d: X \times X \to \R }[/math] which satisfies the axioms for a metric, except that instead of the second (identity of indiscernibles) only [math]\displaystyle{ d(x,x)=0 }[/math] for all [math]\displaystyle{ x }[/math] is required. In other words, the axioms for a pseudometric are:

  1. [math]\displaystyle{ d(x, y) \geq 0 }[/math]
  2. [math]\displaystyle{ d(x,x)=0 }[/math]
  3. [math]\displaystyle{ d(x,y)=d(y,x) }[/math]
  4. [math]\displaystyle{ d(x,z)\leq d(x,y) + d(y,z) }[/math].

In some contexts, pseudometrics are referred to as semimetrics because of their relation to seminorms.

Quasimetrics

Occasionally, a quasimetric is defined as a function that satisfies all axioms for a metric with the possible exception of symmetry.[6] The name of this generalisation is not entirely standardized.[7]

  1. [math]\displaystyle{ d(x, y) \geq 0 }[/math]
  2. [math]\displaystyle{ d(x,y)=0 \iff x=y }[/math]
  3. [math]\displaystyle{ d(x,z) \leq d(x,y) + d(y,z) }[/math]

Quasimetrics are common in real life. For example, given a set [math]\displaystyle{ X }[/math] of mountain villages, the typical walking times between elements of [math]\displaystyle{ X }[/math] form a quasimetric because travel up hill takes longer than travel down hill. Another example is a taxicab geometry topology having one-way streets, where a path from point [math]\displaystyle{ A }[/math] to point [math]\displaystyle{ B }[/math] comprises a different set of streets than a path from [math]\displaystyle{ B }[/math] to [math]\displaystyle{ A }[/math].

A quasimetric on the reals can be defined by setting

[math]\displaystyle{ d(x,y)=\begin{cases} x-y & \text{if }x\geq y,\\ 1 & \text{otherwise.} \end{cases} }[/math]

The 1 may be replaced by infinity or by [math]\displaystyle{ 1 + 10^{(y-x)} }[/math].

The topological space underlying this quasimetric space is the Sorgenfrey line. This space describes the process of filing down a metal stick: it is easy to reduce its size, but it is difficult or impossible to grow it.

If [math]\displaystyle{ d }[/math] is a quasimetric on [math]\displaystyle{ X }[/math], a metric [math]\displaystyle{ d' }[/math] on [math]\displaystyle{ X }[/math] can be formed by taking

[math]\displaystyle{ d'(x,y)=\frac{d(x,y)+d(y,x)}{2} }[/math]

Metametrics

In a metametric, all the axioms of a metric are satisfied except that the distance between identical points is not necessarily zero. In other words, the axioms for a metametric are:

  1. [math]\displaystyle{ d(x,y)\geq 0 }[/math]
  2. [math]\displaystyle{ d(x,y)=0 \implies x=y }[/math]
  3. [math]\displaystyle{ d(x,y)=d(y,x) }[/math]
  4. [math]\displaystyle{ d(x,z)\leq d(x,y)+d(y,z). }[/math]

Metametrics appear in the study of Gromov hyperbolic metric spaces and their boundaries. The visual metametric on such a space satisfies [math]\displaystyle{ d(x,x)=0 }[/math] for points [math]\displaystyle{ x }[/math] on the boundary, but otherwise [math]\displaystyle{ d(x,x) }[/math] is approximately the distance from [math]\displaystyle{ x }[/math] to the boundary. Metametrics were first defined by Jussi Väisälä.[8]

Semimetrics

A semimetric on [math]\displaystyle{ X }[/math] is a function [math]\displaystyle{ d: X \times X \to \R }[/math] that satisfies the first three axioms, but not necessarily the triangle inequality:

  1. [math]\displaystyle{ d(x,y)\geq 0 }[/math]
  2. [math]\displaystyle{ d(x,y)=0 \iff x=y }[/math]
  3. [math]\displaystyle{ d(x,y)=d(y,x) }[/math]

Some authors work with a weaker form of the triangle inequality, such as:

[math]\displaystyle{ d(x,z)\leq \rho\,(d(x,y)+d(y,z)) }[/math] ρ-relaxed triangle inequality
[math]\displaystyle{ d(x,z)\leq \rho\,\max\{d(x,y),d(y,z)\} }[/math] ρ-inframetric inequality

The ρ-inframetric inequality implies the ρ-relaxed triangle inequality (assuming the first axiom), and the ρ-relaxed triangle inequality implies the 2ρ-inframetric inequality. Semimetrics satisfying these equivalent conditions have sometimes been referred to as "quasimetrics",[9] "nearmetrics"[10] or inframetrics.[11]

The ρ-inframetric inequalities were introduced to model round-trip delay times in the internet.[11] The triangle inequality implies the 2-inframetric inequality, and the ultrametric inequality is exactly the 1-inframetric inequality.

Premetrics

Relaxing the last three axioms leads to the notion of a premetric, i.e. a function satisfying the following conditions:

  1. [math]\displaystyle{ d(x,y)\geq 0 }[/math]
  2. [math]\displaystyle{ d(x,x)=0 }[/math]

This is not a standard term. Sometimes it is used to refer to other generalizations of metrics such as pseudosemimetrics[12] or pseudometrics;[13] in translations of Russian books it sometimes appears as "prametric".[14] A premetric that satisfies symmetry, i.e. a pseudosemimetric, is also called a distance.[15]

Any premetric gives rise to a topology as follows. For a positive real [math]\displaystyle{ r }[/math], the [math]\displaystyle{ r }[/math]-ball centered at a point [math]\displaystyle{ p }[/math] is defined as

[math]\displaystyle{ B_r(p)=\{ x | d(x,p) \lt r \}. }[/math]

A set is called open if for any point [math]\displaystyle{ p }[/math] in the set there is an [math]\displaystyle{ r }[/math]-ball centered at [math]\displaystyle{ p }[/math] which is contained in the set. Every premetric space is a topological space, and in fact a sequential space. In general, the [math]\displaystyle{ r }[/math]-balls themselves need not be open sets with respect to this topology. As for metrics, the distance between two sets [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math], is defined as

[math]\displaystyle{ d(A,B)=\underset{x\in A, y\in B}\inf d(x,y). }[/math]

This defines a premetric on the power set of a premetric space. If we start with a (pseudosemi-)metric space, we get a pseudosemimetric, i.e. a symmetric premetric. Any premetric gives rise to a preclosure operator [math]\displaystyle{ cl }[/math] as follows:

[math]\displaystyle{ cl(A)=\{ x | d(x,A) = 0 \}. }[/math]

Pseudoquasimetrics

The prefixes pseudo-, quasi- and semi- can also be combined, e.g., a pseudoquasimetric (sometimes called hemimetric) relaxes both the indiscernibility axiom and the symmetry axiom and is simply a premetric satisfying the triangle inequality. For pseudoquasimetric spaces the open [math]\displaystyle{ r }[/math]-balls form a basis of open sets. A very basic example of a pseudoquasimetric space is the set [math]\displaystyle{ \{0,1\} }[/math] with the premetric given by [math]\displaystyle{ d(0,1) = 1 }[/math] and [math]\displaystyle{ d(1,0) = 0. }[/math] The associated topological space is the Sierpiński space.

Sets equipped with an extended pseudoquasimetric were studied by William Lawvere as "generalized metric spaces".[16] From a categorical point of view, the extended pseudometric spaces and the extended pseudoquasimetric spaces, along with their corresponding nonexpansive maps, are the best behaved of the metric space categories. One can take arbitrary products and coproducts and form quotient objects within the given category. If one drops "extended", one can only take finite products and coproducts. If one drops "pseudo", one cannot take quotients. Approach spaces are a generalization of metric spaces that maintains these good categorical properties.

Łukaszyk-Karmowski distance

Łukaszyk-Karmowski distance is a function defining a distance between two random variables or two random vectors. The axioms of this function are:

  1. [math]\displaystyle{ d(x,y)\gt 0 }[/math]
  2. [math]\displaystyle{ d(x,y)=d(y,x) }[/math]
  3. [math]\displaystyle{ d(x,z)\leq d(x,y)+d(y,z). }[/math]

This distance function satisfies the identity of indiscernibles condition if and only if both arguments are described by idealized Dirac delta density probability distribution functions.

Important cases of generalized metrics

In differential geometry, one considers a metric tensor, which can be thought of as an infinitesimal quadratic metric function. This is defined as a nondegenerate symmetric bilinear form on the tangent space of a manifold with an appropriate differentiability requirement. While these are not metric functions as defined in this article, they induce what is called a pseudo-semimetric function by integration of its square root along a path through the manifold. If one imposes the positive-definiteness requirement of an inner product on the metric tensor, this restricts to the case of a Riemannian manifold, and the path integration yields a metric.

In general relativity the related concept is a metric tensor (general relativity) which expresses the structure of a pseudo-Riemannian manifold. Though the term "metric" is used, the fundamental idea is different because there are non-zero null vectors in the tangent space of these manifolds, and vectors can have negative squared norms. This generalized view of "metrics", in which zero distance does not imply identity, has crept into some mathematical writing too:[17]

See also

Notes

  1. ↑ Čech 1969.
  2. ↑ Narici & Beckenstein 2011, pp. 47–51.
  3. ↑ Narici & Beckenstein 2011, pp. 47-66.
  4. ↑ 4.0 4.1 Vitányi 2011.
  5. ↑ Cohen & Vitányi 2012.
  6. ↑ (Steen Seebach); (Smyth 1987)
  7. ↑ (Rolewicz 1987) calls them "semimetrics". That same term is also frequently used for two other generalizations of metrics.
  8. ↑ Väisälä 2005.
  9. ↑ Xia 2009.
  10. ↑ Xia 2008.
  11. ↑ 11.0 11.1 Fraigniaud, Lebhar & Viennot 2008.
  12. ↑ Buldygin & Kozachenko 2000.
  13. ↑ Helemskii 2006.
  14. ↑ (Arkhangel'skii Pontryagin); (Aldrovandi Pereira)
  15. ↑ Deza & Laurent 1997.
  16. ↑ (Lawvere 2002); (Vickers 2005)
  17. ↑ (Parrott 1987): "This bilinear form is variously called the Lorentz metric, or Minkowski metric or metric tensor"; (Cecil 2008): "We call this scalar product the Lorentz metric"

References

William Lawvere 

| issue = 1
| journal = Reprints in Theory and Applications of Categories
| mr = 1925933
| pages = 1–37
| title = Metric spaces, generalized logic, and closed categories
| url = http://tac.mta.ca/tac/reprints/articles/1/tr1.pdf
| year = 2002}}; reprinted with added commentary from Lawvere, F. William (1973), "Metric spaces, generalized logic, and closed categories", Rendiconti del Seminario Matematico e Fisico di Milano 43:  135–166 (1974), doi:10.1007/BF02924844 

de:Metrik (Mathematik)




Retrieved from "https://handwiki.org/wiki/index.php?title=Metric_(mathematics)&oldid=2236683"