Software:G*Power
From HandWiki
Short description: Statistics software
G*Power is a free-to use software used to calculate statistical power. The program offers the ability to calculate power for a wide variety of statistical tests including t-tests, F-tests, and chi-square-tests, among others. Additionally, the user must determine which of the many contexts this test is being used, such as a one-way ANOVA versus a multi-way ANOVA. In order to calculate power, the user must know four of five variables: either number of groups, number of observations, effect size, significance level (α), or power (1-β). G*Power has a built-in tool for determining effect size if it cannot be estimated from prior literature or is not easily calculable.
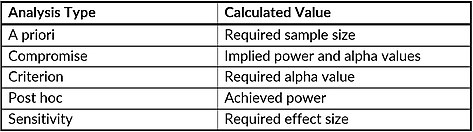
The table lists all possible analyses that the updated G*Power 3.1 can perform for various functions. A priori analyses are one of the most commonly used analyses in research and calculate the needed sample size in order to achieve a sufficient power level and requires inputted values for alpha and effect size. Compromise analyses find implied power based on the beta/alpha ratio, or q, and inputted values for effect size and sample size. Criterion analyses calculate the required alpha value based on the inputted power, effect size, and sample size. Post hoc analyses find actual power based on the inputted alpha, sample size, and effect size. Lastly, sensitivity analyses find the needed effect size given the alpha value, power, and sample size.
References
Further reading
- Faul, F., Erdfelder, E., Lang, A., & Buchner, A. (2007). G*Power 3: A flexible statistical power analysis program for the social, behavioral, and biomedical sciences. Behavior Research Methods, 39(2), 175-191. doi:10.3758/bf03193146
- Faul, F., Erdfelder, E., Buchner, A., & Lang, A. (2009). Statistical power analyses using G*Power 3.1: Tests for correlation and regression analyses. Behavior Research Methods, 41(4), 1149-1160. doi:10.3758/brm.41.4.1149
External links
 |


