Engineering:Double-layer capacitance

Short description: Capacitance present in the interface between a surface and fluid

Double-layer capacitance is the important characteristic of the electrical double layer which appears at the interface between a surface and a fluid (for example, between a conductive electrode and an adjacent liquid electrolyte). At this boundary two layers of electric charge with opposing polarity form, one at the surface of the electrode, and one in the electrolyte. These two layers, electrons on the electrode and ions in the electrolyte, are typically separated by a single layer of solvent molecules that adhere to the surface of the electrode and act like a dielectric in a conventional capacitor. The amount of charge stored in double-layer capacitor depends on the applied voltage.

The double-layer capacitance is the physical principle behind the electrostatic double-layer type of supercapacitors.

History

• Development of the double layer and pseudocapacitance model see Double layer (interfacial)
• Development of the electrochemical components see Supercapacitors

Capacitance

Simplified view of a double-layer of negative ions in the electrode and solvated positive ions in the liquid electrolyte, separated by a layer of polarized solvent molecules.

Helmholtz laid the theoretical foundations for understanding the double layer phenomenon. The formation of double layers is exploited in every electrochemical capacitor to store electrical energy.

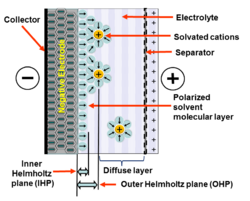
Every capacitor has two electrodes, mechanically separated by a separator. These are electrically connected via the electrolyte, a mixture of positive and negative ions dissolved in a solvent such as water. Where the liquid electrolyte contacts the electrode's conductive metallic surface, an interface is formed which represents a common boundary between the two phases of matter. It is at this interface that the double layer effect occurs.

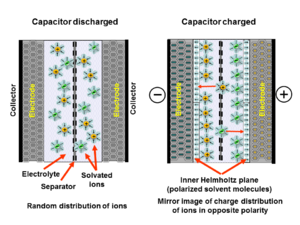
When a voltage is applied to the capacitor, two layers of polarized ions are generated at the electrode interfaces. One layer is within the solid electrode (at the surfaces of crystal grains from which it is made that are in contact with the electrolyte). The other layer, with opposite polarity, forms from dissolved and solvated ions distributed in the electrolyte that have moved towards the polarized electrode. These two layers of polarized ions are separated by a monolayer of solvent molecules. The molecular monolayer forms the inner Helmholtz plane (IHP). It adheres by physical adsorption on the electrode surface and separates the oppositely polarized ions from each other, forming a molecular dielectric.

The amount of charge in the electrode is matched by the magnitude of counter-charges in the outer Helmholtz plane (OHP). This is the area close to the IHP, in which the polarized electrolyte ions are collected. This separation of two layers of polarized ions through the double-layer stores electrical charges in the same way as in a conventional capacitor. The double-layer charge forms a static electric field in the molecular IHP layer of the solvent molecules that corresponds to the strength of the applied voltage.

The "thickness" of a charged layer in the metallic electrode, i.e., the average extension perpendicular to the surface, is about 0.1 nm, and mainly depends on the electron density because the atoms in solid electrodes are stationary. In the electrolyte, the thickness depends on the size of the solvent molecules and of the movement and concentration of ions in the solvent. It ranges from 0.1 to 10 nm as described by the Debye length. The sum of the thicknesses is the total thickness of a double layer.

The IHP's small thickness creates a strong electric field E over the separating solvent molecules. At a potential difference of, for example, U = 2 V and a molecular thickness of d = 0.4 nm, the electric field strength is

[math]\displaystyle{ E = \frac{U}{d} = \frac{2\ \text{V}}{0.4\ \text{nm}} = 5000\ \text{kV/mm} }[/math]

To compare this figure with values from other capacitor types requires an estimation for electrolytic capacitors, the capacitors with the thinnest dielectric among conventional capacitors. The voltage proof of aluminum oxide, the dielectric layer of aluminum electrolytic capacitors, is approximately 1.4 nm/V. For a 6.3 V capacitor therefore the layer is 8.8 nm. The electric field is 6.3 V/8.8 nm = 716 kV/mm, around 7 times lower than in the double-layer. The field strength of some 5000 kV/mm is unrealizable in conventional capacitors. No conventional dielectric material could prevent charge carrier breakthrough. In a double-layer capacitor the chemical stability of the solvent's molecular bonds prevents breakthrough.

The forces that cause the adhesion of solvent molecules in the IHP are physical forces rather than chemical bonds. Chemical bonds exist within the adsorbed molecules, but they are polarized.

The magnitude of the electric charge that can accumulate in the layers corresponds to the concentration of the adsorbed ions and the electrodes surface. Up to the electrolyte's decomposition voltage, this arrangement behaves like a capacitor in which the stored electrical charge is linearly dependent on the voltage.

Structure and function of an ideal double-layer capacitor. Applying a voltage to the capacitor at both electrodes a Helmholtz double-layer will be formed separating the adhered ions in the electrolyte in a mirror charge distribution of opposite polarity

The double-layer is like the dielectric layer in a conventional capacitor, but with the thickness of a single molecule. Using the early Helmholtz model to calculate the capacitance the model predicts a constant differential capacitance C_d independent from the charge density, even depending on the dielectric constant ε and the charge layer separation δ.

[math]\displaystyle{ \ C_d = \frac{\epsilon}{4 \pi \delta} }[/math]

If the electrolyte solvent is water then the influence of the high field strength creates a permittivity ε of 6 (instead of 80 without an applied electric field) and the layer separation δ ca. 0.3 nm, the Helmholtz model predicts a differential capacitance value of about 18 µF/cm². This value can be used to calculate capacitance values using the standard formula for conventional plate capacitors if only the surface of the electrodes is known. This capacitance can be calculated with:

[math]\displaystyle{ C= \frac{\varepsilon A}{d} }[/math].

The capacitance C is greatest in components made from materials with a high permittivity ε, large electrode plate surface areas A and a small distance d between plates. Because activated carbon electrodes have a very high surface area and an extremely thin double-layer distance which is on the order of a few ångströms (0.3-0.8 nm), it is understandable why supercapacitors have the highest capacitance values among the capacitors (in the range of 10 to 40 µF/cm²).

In real produced supercapacitors with a high amount of double-layer capacitance the capacitance value depends first on electrode surface and DL distance. Parameters such as electrode material and structure, electrolyte mixture, and amount of pseudocapacitance also contribute to capacitance value.

Because an electrochemical capacitor is composed out of two electrodes, electric charge in the Helmholtz layer at one electrode is mirrored (with opposite polarity) in the second Helmholtz layer at the second electrode. Therefore, the total capacitance value of a double-layer capacitor is the result of two capacitors connected in series. If both electrodes have approximately the same capacitance value, as in symmetrical supercapacitors, the total value is roughly half that of one electrode.

Literature

• Double layer (surface science)
• Béguin, Francois; Frackowiak, Elzbieta (18 November 2009). "8 Electrical Double-Layer Capacitors and Pseudocapacitors". Carbons for Electrochemical Energy Storage and Conversion Systems. Taylor & Francis. pp. 329–375. doi:10.1201/9781420055405-c8. ISBN 978-1-4200-5307-4. https://books.google.com/books?id=kEP6mAEACAAJ. 
• Müller, Klaus (1963). On the Structure of Charged Interfaces. 274. Graduate School of Arts and Sciences, University of Pennsylvania. pp. 55–79. doi:10.1098/rspa.1963.0114. Bibcode: 1963RSPSA.274...55B. https://books.google.com/books?id=Yd67SgAACAAJ. 
• B. E. Conway (1999) (in de), Electrochemical Supercapacitors: Scientific Fundamentals and Technological Applications, Berlin: Springer, https://books.google.com/books?id=8yvzlr9TqI0C&pg=PA1 
• Leitner, K. W.; Winter, M.; Besenhard, J. O. (2003-12-01). "Composite supercapacitor electrodes". Journal of Solid State Electrochemistry 8 (1): 15–16. doi:10.1007/s10008-003-0412-x. ISSN 1433-0768. 
• Yu., M.; Volfkovich, T. M. (September 2002). "Electrochemical Capacitors". Russian Journal of Electrochemistry 38 (9): 935–959. doi:10.1023/A:1020220425954. ISSN 1608-3342. 
• (in de) Electrochemical Technologies for Energy Storage and Conversion, Band 1, Weinheim