Physics:Dielectric
| Part of a series of articles about |
| Electromagnetism |
|---|
 |
In electromagnetism, a dielectric (or dielectric medium) is an electrical insulator that can be polarised by an applied electric field. When a dielectric material is placed in an electric field, electric charges do not flow through the material as they do in an electrical conductor, because they have no loosely bound, or free, electrons that may drift through the material, but instead they shift, only slightly, from their average equilibrium positions, causing dielectric polarisation. Because of dielectric polarisation, positive charges are displaced in the direction of the field and negative charges shift in the direction opposite to the field. This creates an internal electric field that reduces the overall field within the dielectric itself. If a dielectric is composed of weakly bonded molecules, those molecules not only become polarised, but also reorient so that their symmetry axes align to the field.[1]
The study of dielectric properties concerns storage and dissipation of electric and magnetic energy in materials.[2][3][4] Dielectrics are important for explaining various phenomena in electronics, optics, solid-state physics and cell biophysics.[5][6]
Terminology
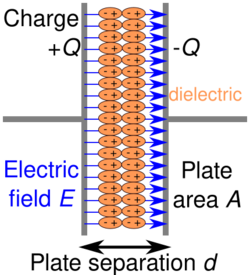
Although the term insulator implies low electrical conduction, dielectric typically means materials with a high polarisability. The latter is expressed by a number called the relative permittivity. Insulator is generally used to indicate electrical obstruction while dielectric is used to indicate the energy storing capacity of the material (by means of polarisation). A common example of a dielectric is the electrically insulating material between the metallic plates of a capacitor. The polarisation of the dielectric by the applied electric field increases the capacitor's surface charge for the given electric field strength.[1]
The term dielectric was coined by William Whewell (from dia + electric) in response to a request from Michael Faraday.[7][8] A perfect dielectric is a material with zero electrical conductivity (cf. perfect conductor infinite electrical conductivity),[9] thus exhibiting only a displacement current; therefore it stores and returns electrical energy as if it were an ideal capacitor.
Electric susceptibility
The electric susceptibility [math]\displaystyle{ \chi_e }[/math] of a dielectric material is a measure of how easily it polarises in response to an electric field. This, in turn, determines the electric permittivity of the material and thus influences many other phenomena in that medium, from the capacitance of capacitors to the speed of light.
It is defined as the constant of proportionality (which may be a tensor) relating an electric field [math]\displaystyle{ \mathbf{E} }[/math] to the induced dielectric polarisation density [math]\displaystyle{ \mathbf{P} }[/math] such that
[math]\displaystyle{ \mathbf{P} = \varepsilon_0 \chi_e \mathbf{E}, }[/math]
where [math]\displaystyle{ \varepsilon_0 }[/math] is the electric permittivity of free space.
The susceptibility of a medium is related to its relative permittivity [math]\displaystyle{ \varepsilon_r }[/math] by
[math]\displaystyle{ \chi_e\ = \varepsilon_r - 1. }[/math]
So in the case of a classical vacuum,
[math]\displaystyle{ \chi_e\ = 0. }[/math]
The electric displacement [math]\displaystyle{ \mathbf{D} }[/math] is related to the polarisation density [math]\displaystyle{ \mathbf{P} }[/math] by
[math]\displaystyle{ \mathbf{D} \ = \ \varepsilon_0 \mathbf{E} + \mathbf{P} \ = \ \varepsilon_0 \left(1 + \chi_e\right) \mathbf{E} \ = \ \varepsilon_0 \varepsilon_r \mathbf{E}. }[/math]
Dispersion and causality
In general, a material cannot polarise instantaneously in response to an applied field. The more general formulation as a function of time is
[math]\displaystyle{ \mathbf{P}(t) = \varepsilon_0 \int_{-\infty}^t \chi_e\left(t - t'\right) \mathbf{E}(t')\, dt'. }[/math]
That is, the polarisation is a convolution of the electric field at previous times with time-dependent susceptibility given by [math]\displaystyle{ \chi_e (\Delta t) }[/math]. The upper limit of this integral can be extended to infinity as well if one defines [math]\displaystyle{ \chi_e (\Delta t) = 0 }[/math] for [math]\displaystyle{ \Delta t \lt 0 }[/math]. An instantaneous response corresponds to Dirac delta function susceptibility [math]\displaystyle{ \chi_e (\Delta t) = \chi_e \delta (\Delta t) }[/math] .
It is more convenient in a linear system to take the Fourier transform and write this relationship as a function of frequency. Due to the convolution theorem, the integral becomes a simple product, [math]\displaystyle{ \mathbf{P}(\omega) = \varepsilon_0 \chi_e(\omega) \mathbf{E}(\omega). }[/math]
The susceptibility (or equivalently the permittivity) is frequency dependent. The change of susceptibility with respect to frequency characterises the dispersion properties of the material.
Moreover, the fact that the polarisation can only depend on the electric field at previous times (i.e., [math]\displaystyle{ \chi_e (\Delta t) = 0 }[/math] for [math]\displaystyle{ \Delta t \lt 0 }[/math]), a consequence of causality, imposes Kramers–Kronig constraints on the real and imaginary parts of the susceptibility [math]\displaystyle{ \chi_e (\omega) }[/math].
Dielectric polarisation
Basic atomic model
In the classical approach to the dielectric, the material is made up of atoms. Each atom consists of a cloud of negative charge (electrons) bound to and surrounding a positive point charge at its center. In the presence of an electric field, the charge cloud is distorted, as shown in the top right of the figure.
This can be reduced to a simple dipole using the superposition principle. A dipole is characterised by its dipole moment, a vector quantity shown in the figure as the blue arrow labeled M. It is the relationship between the electric field and the dipole moment that gives rise to the behaviour of the dielectric. (Note that the dipole moment points in the same direction as the electric field in the figure. This isn't always the case, and is a major simplification, but is true for many materials.)
When the electric field is removed, the atom returns to its original state. The time required to do so is called relaxation time; an exponential decay.
This is the essence of the model in physics. The behaviour of the dielectric now depends on the situation. The more complicated the situation, the richer the model must be to accurately describe the behaviour. Important questions are:
- Is the electric field constant, or does it vary with time? At what rate?
- Does the response depend on the direction of the applied field (isotropy of the material)?
- Is the response the same everywhere (homogeneity of the material)?
- Do any boundaries or interfaces have to be taken into account?
- Is the response linear with respect to the field, or are there nonlinearities?
The relationship between the electric field E and the dipole moment M gives rise to the behaviour of the dielectric, which, for a given material, can be characterised by the function F defined by the equation: [math]\displaystyle{ \mathbf{M} = \mathbf{F}(\mathbf{E}). }[/math]
When both the type of electric field and the type of material have been defined, one then chooses the simplest function F that correctly predicts the phenomena of interest. Examples of phenomena that can be so modelled include:
Dipolar polarisation
Dipolar polarisation is a polarisation that is either inherent to polar molecules (orientation polarisation), or can be induced in any molecule in which the asymmetric distortion of the nuclei is possible (distortion polarisation). Orientation polarisation results from a permanent dipole, e.g., that arising from the 104.45° angle between the asymmetric bonds between oxygen and hydrogen atoms in the water molecule, which retains polarisation in the absence of an external electric field. The assembly of these dipoles forms a macroscopic polarisation.
When an external electric field is applied, the distance between charges within each permanent dipole, which is related to chemical bonding, remains constant in orientation polarisation; however, the direction of polarisation itself rotates. This rotation occurs on a timescale that depends on the torque and surrounding local viscosity of the molecules. Because the rotation is not instantaneous, dipolar polarisations lose the response to electric fields at the highest frequencies. A molecule rotates about 1 radian per picosecond in a fluid, thus this loss occurs at about 1011 Hz (in the microwave region). The delay of the response to the change of the electric field causes friction and heat.
When an external electric field is applied at infrared frequencies or less, the molecules are bent and stretched by the field and the molecular dipole moment changes. The molecular vibration frequency is roughly the inverse of the time it takes for the molecules to bend, and this distortion polarisation disappears above the infrared.
Ionic polarisation
Ionic polarisation is polarisation caused by relative displacements between positive and negative ions in ionic crystals (for example, NaCl).
If a crystal or molecule consists of atoms of more than one kind, the distribution of charges around an atom in the crystal or molecule leans to positive or negative. As a result, when lattice vibrations or molecular vibrations induce relative displacements of the atoms, the centers of positive and negative charges are also displaced. The locations of these centers are affected by the symmetry of the displacements. When the centers don't correspond, polarisation arises in molecules or crystals. This polarisation is called ionic polarisation.
Ionic polarisation causes the ferroelectric effect as well as dipolar polarisation. The ferroelectric transition, which is caused by the lining up of the orientations of permanent dipoles along a particular direction, is called an order-disorder phase transition. The transition caused by ionic polarisations in crystals is called a displacive phase transition.
In cells
Ionic polarisation enables the production of energy-rich compounds in cells (the proton pump in mitochondria) and, at the plasma membrane, the establishment of the resting potential, energetically unfavourable transport of ions, and cell-to-cell communication (the Na+/K+-ATPase).
All cells in animal body tissues are electrically polarised – in other words, they maintain a voltage difference across the cell's plasma membrane, known as the membrane potential. This electrical polarisation results from a complex interplay between ion transporters and ion channels.
In neurons, the types of ion channels in the membrane usually vary across different parts of the cell, giving the dendrites, axon, and cell body different electrical properties. As a result, some parts of the membrane of a neuron may be excitable (capable of generating action potentials), whereas others are not.
Dielectric dispersion
In physics, dielectric dispersion is the dependence of the permittivity of a dielectric material on the frequency of an applied electric field. Because there is a lag between changes in polarisation and changes in the electric field, the permittivity of the dielectric is a complex function of the frequency of the electric field. Dielectric dispersion is very important for the applications of dielectric materials and the analysis of polarisation systems.
This is one instance of a general phenomenon known as material dispersion: a frequency-dependent response of a medium for wave propagation.
When the frequency becomes higher:
- The dipolar polarisation can no longer follow the oscillations of the electric field in the microwave region around 1010 Hz,
- The ionic polarisation and molecular distortion polarisation can no longer track the electric field past the infrared or far-infrared region around 1013 Hz,
- The electronic polarisation loses its response in the ultraviolet region around 1015 Hz.
In the frequency region above ultraviolet, permittivity approaches the constant ε0 in every substance, where ε0 is the permittivity of the free space. Because permittivity indicates the strength of the relation between an electric field and polarisation, if a polarisation process loses its response, permittivity decreases.
Dielectric relaxation
Dielectric relaxation is the momentary delay (or lag) in the dielectric constant of a material. This is usually caused by the delay in molecular polarisation with respect to a changing electric field in a dielectric medium (e.g., inside capacitors or between two large conducting surfaces). Dielectric relaxation in changing electric fields could be considered analogous to hysteresis in changing magnetic fields (e.g., in inductor or transformer cores). Relaxation in general is a delay or lag in the response of a linear system, and therefore dielectric relaxation is measured relative to the expected linear steady state (equilibrium) dielectric values. The time lag between electrical field and polarisation implies an irreversible degradation of Gibbs free energy.
In physics, dielectric relaxation refers to the relaxation response of a dielectric medium to an external, oscillating electric field. This relaxation is often described in terms of permittivity as a function of frequency, which can, for ideal systems, be described by the Debye equation. On the other hand, the distortion related to ionic and electronic polarisation shows behaviour of the resonance or oscillator type. The character of the distortion process depends on the structure, composition, and surroundings of the sample.
Debye relaxation
Debye relaxation is the dielectric relaxation response of an ideal, noninteracting population of dipoles to an alternating external electric field. It is usually expressed in the complex permittivity ε of a medium as a function of the field's angular frequency ω:
[math]\displaystyle{ \hat{\varepsilon}(\omega) = \varepsilon_{\infty} + \frac{\Delta\varepsilon}{1 + i\omega\tau}, }[/math]
where ε∞ is the permittivity at the high frequency limit, Δε = εs − ε∞ where εs is the static, low frequency permittivity, and τ is the characteristic relaxation time of the medium. Separating into the real part [math]\displaystyle{ \varepsilon' }[/math] and the imaginary part [math]\displaystyle{ \varepsilon'' }[/math] of the complex dielectric permittivity yields:[10]
[math]\displaystyle{ \begin{align} \varepsilon' &= \varepsilon_\infty + \frac{\varepsilon_s - \varepsilon_\infty}{1 + \omega^2\tau^2} \\[3pt] \varepsilon'' &= \frac{(\varepsilon_s - \varepsilon_\infty)\omega\tau}{1+\omega^2\tau^2} \end{align} }[/math]
Note that the above equation for [math]\displaystyle{ \hat{\varepsilon}(\omega) }[/math]is sometimes written with [math]\displaystyle{ 1 - i\omega\tau }[/math] in the denominator due to an ongoing sign convention ambiguity whereby many sources represent the time dependence of the complex electric field with [math]\displaystyle{ \exp(-i\omega t) }[/math] whereas others use [math]\displaystyle{ \exp(+i\omega t) }[/math]. In the former convention, the functions [math]\displaystyle{ \varepsilon' }[/math] and [math]\displaystyle{ \varepsilon'' }[/math] representing real and imaginary parts are given by [math]\displaystyle{ \hat{\varepsilon}(\omega)=\varepsilon'+ i \varepsilon'' }[/math] whereas in the latter convention [math]\displaystyle{ \hat{\varepsilon}(\omega)=\varepsilon'- i \varepsilon'' }[/math]. The above equation uses the latter convention.[11]
The dielectric loss is also represented by the loss tangent:
[math]\displaystyle{ \tan(\delta) = \frac{\varepsilon''}{\varepsilon'} = \frac{\left(\varepsilon_s - \varepsilon_\infty\right)\omega\tau}{\varepsilon_s + \varepsilon_\infty \omega^2 \tau^2} }[/math]
This relaxation model was introduced by and named after the physicist Peter Debye (1913).[12] It is characteristic for dynamic polarisation with only one relaxation time.
Variants of the Debye equation
- Cole–Cole equation
- This equation is used when the dielectric loss peak shows symmetric broadening.
- Cole–Davidson equation
- This equation is used when the dielectric loss peak shows asymmetric broadening.
- Havriliak–Negami relaxation
- This equation considers both symmetric and asymmetric broadening.
- Kohlrausch–Williams–Watts function
- Fourier transform of stretched exponential function.
- Curie–von Schweidler law
- This shows the response of dielectrics to an applied DC field to behave according to a power law, which can be expressed as an integral over weighted exponential functions.
- Djordjevic–Sarkar approximation
- This is used when the dielectric loss is approximately constant for a wide range of frequencies.
Paraelectricity
Paraelectricity is the nominal behaviour of dielectrics when the dielectric permittivity tensor is proportional to the unit matrix, i.e., an applied electric field causes polarisation and/or alignment of dipoles only parallel to the applied electric field. Contrary to the analogy with a paramagnetic material, no permanent electric dipole needs to exist in a paraelectric material. Removal of the fields results in the dipolar polarisation returning to zero.[13] The mechanisms that causes paraelectric behaviour are distortion of individual ions (displacement of the electron cloud from the nucleus) and polarisation of molecules or combinations of ions or defects.
Paraelectricity can occur in crystal phases where electric dipoles are unaligned and thus have the potential to align in an external electric field and weaken it.
Most dielectric materials are paraelectrics. A specific example of a paraelectric material of high dielectric constant is strontium titanate.
The LiNbO3 crystal is ferroelectric below 1430 K, and above this temperature it transforms into a disordered paraelectric phase. Similarly, other perovskites also exhibit paraelectricity at high temperatures.
Paraelectricity has been explored as a possible refrigeration mechanism; polarising a paraelectric by applying an electric field under adiabatic process conditions raises the temperature, while removing the field lowers the temperature.[14] A heat pump that operates by polarising the paraelectric, allowing it to return to ambient temperature (by dissipating the extra heat), bringing it into contact with the object to be cooled, and finally depolarising it, would result in refrigeration.
Tunability
Tunable dielectrics are insulators whose ability to store electrical charge changes when a voltage is applied.[15]
Generally, strontium titanate (SrTiO3) is used for devices operating at low temperatures, while barium strontium titanate (Ba1−xSrxTiO3) substitutes for room temperature devices. Other potential materials include microwave dielectrics and carbon nanotube (CNT) composites.[15][16][17]
In 2013, multi-sheet layers of strontium titanate interleaved with single layers of strontium oxide produced a dielectric capable of operating at up to 125 GHz. The material was created via molecular beam epitaxy. The two have mismatched crystal spacing that produces strain within the strontium titanate layer that makes it less stable and tunable.[15]
Systems such as Ba1−xSrxTiO3 have a paraelectric–ferroelectric transition just below ambient temperature, providing high tunability. Films suffer significant losses arising from defects.
Applications
Capacitors
Commercially manufactured capacitors typically use a solid dielectric material with high permittivity as the intervening medium between the stored positive and negative charges. This material is often referred to in technical contexts as the capacitor dielectric.[18]
The most obvious advantage to using such a dielectric material is that it prevents the conducting plates, on which the charges are stored, from coming into direct electrical contact. More significantly, however, a high permittivity allows a greater stored charge at a given voltage. This can be seen by treating the case of a linear dielectric with permittivity ε and thickness d between two conducting plates with uniform charge density σε. In this case the charge density is given by
[math]\displaystyle{ \sigma_{\varepsilon}=\varepsilon\frac{V}{d} }[/math]
and the capacitance per unit area by
[math]\displaystyle{ c=\frac{\sigma_{\varepsilon}}{V}=\frac{\varepsilon}{d} }[/math]
From this, it can easily be seen that a larger ε leads to greater charge stored and thus greater capacitance.
Dielectric materials used for capacitors are also chosen such that they are resistant to ionisation. This allows the capacitor to operate at higher voltages before the insulating dielectric ionises and begins to allow undesirable current.
Dielectric resonator
A dielectric resonator oscillator (DRO) is an electronic component that exhibits resonance of the polarisation response for a narrow range of frequencies, generally in the microwave band. It consists of a "puck" of ceramic that has a large dielectric constant and a low dissipation factor. Such resonators are often used to provide a frequency reference in an oscillator circuit. An unshielded dielectric resonator can be used as a dielectric resonator antenna (DRA).
BST thin films
From 2002 to 2004, the United States Army Research Laboratory (ARL) conducted research on thin film technology. Barium strontium titanate (BST), a ferroelectric thin film, was studied for the fabrication of radio frequency and microwave components, such as voltage-controlled oscillators, tunable filters and phase shifters.[19]
The research was part of an effort to provide the Army with highly-tunable, microwave-compatible materials for broadband electric-field tunable devices, which operate consistently in extreme temperatures.[20] This work improved tunability of bulk barium strontium titanate, which is a thin film enabler for electronics components.[21]
In a 2004 research paper, U.S. ARL researchers explored how small concentrations of acceptor dopants can dramatically modify the properties of ferroelectric materials such as BST.[22]
Researchers "doped" BST thin films with magnesium, analyzing the "structure, microstructure, surface morphology and film/substrate compositional quality" of the result. The Mg doped BST films showed "improved dielectric properties, low leakage current, and good tunability", meriting potential for use in microwave tunable devices.[19]
Some practical dielectrics
Dielectric materials can be solids, liquids, or gases. (A high vacuum can also be a useful,[23] nearly lossless dielectric even though its relative dielectric constant is only unity.)
Solid dielectrics are perhaps the most commonly used dielectrics in electrical engineering, and many solids are very good insulators. Some examples include porcelain, glass, and most plastics. Air, nitrogen and sulfur hexafluoride are the three most commonly used gaseous dielectrics.
- Industrial coatings such as Parylene provide a dielectric barrier between the substrate and its environment.
- Mineral oil is used extensively inside electrical transformers as a fluid dielectric and to assist in cooling. Dielectric fluids with higher dielectric constants, such as electrical grade castor oil, are often used in high voltage capacitors to help prevent corona discharge and increase capacitance.
- Because dielectrics resist the flow of electricity, the surface of a dielectric may retain stranded excess electrical charges. This may occur accidentally when the dielectric is rubbed (the triboelectric effect). This can be useful, as in a Van de Graaff generator or electrophorus, or it can be potentially destructive as in the case of electrostatic discharge.
- Specially processed dielectrics, called electrets (which should not be confused with ferroelectrics), may retain excess internal charge or "frozen in" polarisation. Electrets have a semi-permanent electric field, and are the electrostatic equivalent to magnets. Electrets have numerous practical applications in the home and industry.
- Some dielectrics can generate a potential difference when subjected to mechanical stress, or (equivalently) change physical shape if an external voltage is applied across the material. This property is called piezoelectricity. Piezoelectric materials are another class of very useful dielectrics.
- Some ionic crystals and polymer dielectrics exhibit a spontaneous dipole moment, which can be reversed by an externally applied electric field. This behaviour is called the ferroelectric effect. These materials are analogous to the way ferromagnetic materials behave within an externally applied magnetic field. Ferroelectric materials often have very high dielectric constants, making them quite useful for capacitors.
See also
- Classification of materials based on permittivity
- Paramagnetism
- Clausius-Mossotti relation
- Dielectric absorption
- Dielectric losses
- Dielectric strength
- Dielectric spectroscopy
- EIA Class 1 dielectric
- EIA Class 2 dielectric
- High-κ dielectric
- Low-κ dielectric
- leakage
- Linear response function
- Metamaterial
- RC delay
- Rotational Brownian motion
- Paschen's law – variation of dielectric strength of gas related to pressure
- Separator (electricity)
References
- ↑ Jump up to: 1.0 1.1 "Dielectric". Encyclopædia Britannica. Chicago , Illinois: Encyclopædia Britannica, Inc.. https://global.britannica.com/science/dielectric. Retrieved 20 November 2021. "Dielectric, insulating material or a very poor conductor of electric current. When dielectrics are placed in an electric field, practically no current flows in them.".
- ↑ Arthur R. von Hippel, in his seminal work, Dielectric Materials and Applications, stated: "Dielectrics... are not a narrow class of so-called insulators, but the broad expanse of nonmetals considered from the standpoint of their interaction with electric, magnetic or electromagnetic fields. Thus we are concerned with gases as well as with liquids and solids and with the storage of electric and magnetic energy as well as its dissipation." (p. 1) (Technology Press of MIT and John Wiley, NY, 1954).
- ↑ Thoms, E.; Sippel, P.; et., al. (2017). "Dielectric study on mixtures of ionic liquids". Sci. Rep. 7 (1): 7463. doi:10.1038/s41598-017-07982-3. PMID 28785071. Bibcode: 2017NatSR...7.7463T.
- ↑ Belkin, A.; Bezryadin, A.; Hendren, L.; Hubler, A. (2017). "Recovery of Alumina Nanocapacitors after High and Low Voltage Breakdown". Sci. Rep. 7 (1): 932. doi:10.1038/s41598-017-01007-9. PMID 28428625. Bibcode: 2017NatSR...7..932B.
- ↑ Hossain, Shadeeb (2020-12-27). "Malignant cell characterisation via mathematical analysis of bio impedance and optical properties". Electromagnetic Biology and Medicine 40 (1): 65–83. doi:10.1080/15368378.2020.1850471. ISSN 1536-8378. PMID 33356700. https://doi.org/10.1080/15368378.2020.1850471.
- ↑ Hossain, Shadeeb (2020-04-02). "Biodielectric phenomenon for actively differentiating malignant and normal cells: An overview". Electromagnetic Biology and Medicine 39 (2): 89–96. doi:10.1080/15368378.2020.1737804. ISSN 1536-8378. PMID 32138569. https://doi.org/10.1080/15368378.2020.1737804.
- ↑ Daintith, J. (1994). Biographical Encyclopedia of Scientists. CRC Press. p. 943. ISBN 978-0-7503-0287-6.
- ↑ James, Frank A.J.L., editor. The Correspondence of Michael Faraday, Volume 3, 1841–1848, "Letter 1798, William Whewell to Faraday, p. 442.". http://hermital.org/book/holoprt5-1.htm#F5.8. The Institution of Electrical Engineers, London, United Kingdom, 1996. ISBN:0-86341-250-5
- ↑ Microwave Engineering – R. S. Rao (Prof.). https://books.google.com/books?id=ZecSEXlJE0YC&pg=PA21. Retrieved 2013-11-08.
- ↑ Kao, Kwan Chi (2004). Dielectric Phenomena in Solids. London: Elsevier Academic Press. pp. 92–93. ISBN 978-0-12-396561-5.
- ↑ Böttcher, C.J.F. (1952). Theory of Electric Polarisation. London: Elsevier Publishing Companys. pp. 231-232,348-349.
- ↑ Debye, P. (1913), Ver. Deut. Phys. Gesell. 15, 777; reprinted 1954 in collected papers of Peter J.W. Debye. Interscience, New York
- ↑ Chiang, Y. (1997). Physical Ceramics. New York: John Wiley & Sons.
- ↑ Kuhn, U.; Lüty, F. (1965). "Paraelectric heating and cooling with OH—dipoles in alkali halides". Solid State Communications 3 (2): 31. doi:10.1016/0038-1098(65)90060-8. Bibcode: 1965SSCom...3...31K.
- ↑ Jump up to: 15.0 15.1 15.2 Lee, Che-Hui; Orloff, Nathan D.; Birol, Turan; Zhu, Ye; Goian, Veronica; Rocas, Eduard; Haislmaier, Ryan; Vlahos, Eftihia et al. (2013). "Exploiting dimensionality and defect mitigation to create tunable microwave dielectrics". Nature 502 (7472): 532–536. doi:10.1038/nature12582. PMID 24132232. Bibcode: 2013Natur.502..532L.
- ↑ Kong, L. B.; Li, S.; Zhang, T. S.; Zhai, J. W.; Boey, F. Y. C.; Ma, J. (2010-11-30). "Electrically tunable dielectric materials and strategies to improve their performances". Progress in Materials Science 55 (8): 840–893. doi:10.1016/j.pmatsci.2010.04.004.
- ↑ Giere, A.; Zheng, Y.; Maune, H.; Sazegar, M.; Paul, F.; Zhou, X.; Binder, J. R.; Muller, S. et al. (2008). "Tunable dielectrics for microwave applications". 2008 17th IEEE International Symposium on the Applications of Ferroelectrics. pp. 1. doi:10.1109/ISAF.2008.4693753. ISBN 978-1-4244-2744-4.
- ↑ Müssig, Hans-Joachim. Semiconductor capacitor with praseodymium oxide as dielectric, U.S. Patent 7,113,388 published 2003-11-06, issued 2004-10-18, assigned to IHP GmbH- Innovations for High Performance Microelectronics/Institute Fur Innovative Mikroelektronik
- ↑ Jump up to: 19.0 19.1 Cole, M. W.; Geyer, R. G. (2004). "Novel tunable acceptor doped BST thin films for high quality tunable microwave devices". Revista Mexicana de Fisica 50 (3): 232. Bibcode: 2004RMxF...50..232C.
- ↑ Nair, K. M.; Guo, Ruyan; Bhalla, Amar S.; Hirano, S.-I.; Suvorov, D. (2012-04-11) (in en). Developments in Dielectric Materials and Electronic Devices: Proceedings of the 106th Annual Meeting of The American Ceramic Society, Indianapolis, Indiana, USA 2004. John Wiley & Sons. ISBN 9781118408193. https://books.google.com/books?id=XzZLtRlUPNoC&q=tunable+microwave+devices+army+research+laboratory&pg=PA57.
- ↑ Nair, K. M.; Bhalla, Amar S.; Hirano, S.-I.; Suvorov, D.; Schwartz, Robert W.; Zhu, Wei (2012-04-11) (in en). Ceramic Materials and Multilayer Electronic Devices. John Wiley & Sons. ISBN 9781118406762. https://books.google.com/books?id=gt_4CiNliKEC&q=tunable+microwave+devices+army+research+laboratory&pg=PA229.
- ↑ Cole, M. W.; Hubbard, C.; Ngo, E.; Ervin, M.; Wood, M.; Geyer, R. G. (July 2002). "Structure–property relationships in pure and acceptor-doped Ba1−xSrxTiO3 thin films for tunable microwave device applications" (in en). Journal of Applied Physics 92 (1): 475–483. doi:10.1063/1.1484231. ISSN 0021-8979. Bibcode: 2002JAP....92..475C.
- ↑ Lyon, David (2013). "Gap size dependence of the dielectric strength in nano vacuum gaps". IEEE Transactions on Dielectrics and Electrical Insulation 20 (4): 1467–1471. doi:10.1109/TDEI.2013.6571470.
Further reading
- Jackson, John David (10 August 1998). Classical Electrodynamics (3rd ed.). John Wiley & Sons. ISBN 978-0-471-30932-1. OCLC 535998. https://books.google.com/books?id=FOBBEAAAQBAJ.
- Scaife, Brendan K. P. (3 September 1998). Principles of Dielectrics. Monographs on the Physics & Chemistry of Materials (2nd ed.). Oxford University Press. ISBN 978-0-198-56557-4. https://books.google.com/books?id=9GBP9uBwpScC.
External links
- Feynman's lecture on dielectrics
- Dielectric Sphere in an Electric Field
- Dissemination of IT for the Promotion of Materials Science (DoITPoMS) Teaching and Learning Package "Dielectric Materials" from the University of Cambridge
 Texts on Wikisource:
Texts on Wikisource:
- "Dielectric". Encyclopedia Americana. 1920.
 |