Physics:Shneider-Miles scattering

Shneider-Miles scattering (also referred to as collisional scattering or quasi-Rayleigh scattering) is the quasi-elastic scattering of electromagnetic radiation by charged particles in a small-scale medium with frequent particle collisions. Collisional scattering typically occurs in coherent microwave scattering of high neutral density, low ionization degree microplasmas such as atmospheric pressure laser-induced plasmas. Shneider-Miles scattering is characterized by a 90° phase shift between the incident and scattered waves and a scattering cross section proportional to the square of the incident driving frequency ([math]\displaystyle{ \omega^2 }[/math]). Scattered waves are emitted in a short dipole radiation pattern. The variable phase shift present in semi-collisional scattering regimes allows for determination of a plasma's collisional frequency through coherent microwave scattering.

History

Mikhail Shneider and Richard Miles first described the phenomenon mathematically in their 2005 work on microwave diagnostics of small plasma objects. The scattering regime was experimentally demonstrated and formally named by Adam R. Patel and Alexey Shashurin and has been applied in the coherent microwave scattering diagnosis of small laser-induced plasma objects.

Physical description

Electron Motion in a Plasma Object During One Half-Cycle of Incident Radiation

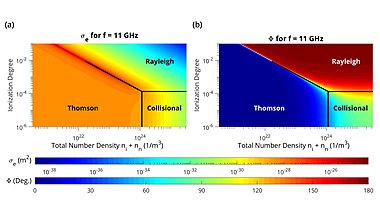
A plasma, consisting of neutral particles, ions, and unbound electrons, responds to the oscillating electric field of incident electromagnetic radiation primarily through the motion of electrons (ions and neutral particles can often be regarded as stationary due to their larger mass). If the frequency of the incident radiation is sufficiently low and the plasma frequency is sufficiently high (corresponding to the Rayleigh scattering regime), the electrons will travel until the plasma object becomes polarized, counteracting the incident electric field and preventing further movement until the incident field reverses direction. If the frequency of the incident radiation is sufficiently high and the plasma frequency is sufficiently low (corresponding to the Thomson scattering regime), electrons will only travel a short distance before the electric field reverses direction, making collisions with other particles unlikely during a given oscillation.

If the frequency on the incident radiation is intermediate and a high density of neutral particles and ions is present, electrons will travel far enough to collide many times with other particles but not far enough to significantly polarize the plasma object. This characterizes the collisional scattering regime. The linear oscillation of unbound electrons in a relatively-small space gives rise to a short-dipole radiation pattern.

This is analogous to a spring-mass-damper system, where the polarization of the plasma object creates the restoring force and the drag due to collisions with other particles creates the damping force. The phase shift of the scattered wave is 90º in the Shneider-Miles regime due to the drag force being dominant.

Note that, in this context, Rayleigh scattering is regarded as [math]\displaystyle{ \omega^4 }[/math] volumetric small particle scattering rather than an even broader short-dipole approximation of the radiation. Otherwise, Thomson scattering would fall under the banner of "Rayleigh". Mie scattering experiences a similar ambiguity.

Mathematical description

Scattering Phase Shifts Become Collisional at High Collisional Frequencies and Low Plasma Frequencies

Scattering Cross Section and Phase Shift for Electrons with 11GHz Incident Microwaves

The scattering cross section of an object ([math]\displaystyle{ \sigma }[/math]) is defined by the time-averaged power of the scattered wave ([math]\displaystyle{ \langle P_s \rangle }[/math]) divided by the intensity of the incident wave ([math]\displaystyle{ I_I }[/math]): [math]\displaystyle{ \sigma=\frac{\langle P_s \rangle}{I_I} }[/math].

Starting with the assumptions that a plasma object is small relative to the incident wavelength, thin relative to the skin depth, unmagnetized, and homogenous, the scattering cross-section of the plasma object can be determined by the following equation, where [math]\displaystyle{ e }[/math] is the electron charge, [math]\displaystyle{ m }[/math] is the electron mass, [math]\displaystyle{ N_e }[/math] is the number of unbound electrons in the plasma object, [math]\displaystyle{ \xi }[/math] is the geometrically-determined depolarization factor, [math]\displaystyle{ \omega }[/math] is the incident wave circular frequency, [math]\displaystyle{ \omega_p }[/math] is the plasma frequency, and [math]\displaystyle{ \nu_m }[/math] is the effective momentum-transfer collisional frequency (not to be confused with collisional frequency).

[math]\displaystyle{ \sigma= \frac{e^4}{6\pi m^2\epsilon_0^2c^4} \frac{N_e^4\omega^4} {(\xi\omega_p^2-\omega^2)^2+(\nu_m\omega)^2} }[/math]

(The above equation is derived from the Drude-Lorentz-Sommerfeld model. It neglects transient effects of electron motion and is only qualitatively applicable to Rayleigh scattering due to neglecting evanescence effects - strict consideration of boundary conditions is often required to capture the case of negative permittivity.). The total cross section can related to the cross section of an individual electron ([math]\displaystyle{ \sigma_e }[/math]) according to the equation [math]\displaystyle{ \sigma_e= \sigma/N_e^2 }[/math], since the electron motion will be in phase assuming that the plasma object is small relative to the incident wavelength.

The scattering regime is determined by the dominant term in the denominator. Collisional scattering refers to the assumption that [math]\displaystyle{ \nu_m\omega\gg|\xi\omega_p^2-\omega| }[/math], allowing the total scattering cross section to be expressed as:

[math]\displaystyle{ \sigma_{collisional}= \frac{e^4}{6\pi m^2\epsilon_0^2c^4} \frac{N_e^4\omega^2} {\nu_m^2} }[/math]

The collisional scattering cross-section can also be expressed in terms of the Thomson scattering cross section ([math]\displaystyle{ \sigma_{Thompson} }[/math]), which is independent of the plasma geometry and collisional frequency according to the following equation.

[math]\displaystyle{ \sigma_{collisional}= \sigma_{Thompson}(\frac{\omega}{\nu_m})^2 }[/math]