Physics:Frenkel–Kontorova model

Short description: Fundamental model of low-dimensional nonlinear physics

The Frenkel–Kontorova model, also known as the FK model, is a fundamental model of low-dimensional nonlinear physics.

The generalized FK model describes a chain of classical particles with nearest neighbor interactions and subjected to a periodic on-site substrate potential. In its original and simplest form the interactions are taken to be harmonic and the potential to be sinusoidal with a periodicity commensurate with the equilibrium distance of the particles. Different choices for the interaction and substrate potentials and inclusion of a driving force may describe a wide range of different physical situations.

Originally introduced by Yakov Frenkel and Tatiana Kontorova in 1938 to describe the structure and dynamics of a crystal lattice near a dislocation core, the FK model has become one of the standard models in condensed matter physics due to its applicability to describe many physical phenomena. Physical phenomena that can be modeled by FK model include dislocations, the dynamics of adsorbate layers on surfaces, crowdions, domain walls in magnetically ordered structures, long Josephson junctions, hydrogen-bonded chains, and DNA type chains. A modification of the FK model, the Tomlinson model, plays an important role in the field of tribology.

The equations for stationary configurations of the FK model reduce to those of the standard map or Chirikov–Taylor map of stochastic theory.

In the continuum-limit approximation the FK model reduces to the exactly integrable sine-Gordon (SG) equation, which allows for soliton solutions. For this reason the FK model is also known as the "discrete sine-Gordon" or "periodic Klein–Gordon equation".

History

A simple model of a harmonic chain in a periodic substrate potential was proposed by Ulrich Dehlinger in 1928. Dehlinger derived an approximate analytical expression for the stable solutions of this model, which he termed Verhakungen, which correspond to what is today called kink pairs. An essentially similar model was developed by Ludwig Prandtl in 1912/13 but did not see publication until 1928.

The model was independently proposed by Yakov Frenkel and Tatiana Kontorova in their 1938 article On the theory of plastic deformation and twinning to describe the dynamics of a crystal lattice near a dislocation and to describe crystal twinning. In the standard linear harmonic chain any displacement of the atoms will result in waves, and the only stable configuration will be the trivial one. For the nonlinear chain of Frenkel and Kontorova, there exist stable configurations beside the trivial one. For small atomic displacements the situation resembles the linear chain; however, for large enough displacements, it is possible to create a moving single dislocation, for which an analytical solution was derived by Frenkel and Kontorova. The shape of these dislocations is defined only by the parameters of the system such as the mass and the elastic constant of the springs.

Dislocations, also called solitons, are distributed non-local defects and mathematically are a type of topological defect. The defining characteristic of solitons/dislocations is that they behave much like stable particles, they can move while maintaining their overall shape. Two solitons of equal and opposite orientation may cancel upon collision, but a single soliton can not annihilate spontaneously.

Generalized model

The generalized FK model treats a one-dimensional chain of atoms with nearest-neighbor interaction in periodic on-site potential, the Hamiltonian for this system is

[math]\displaystyle{ \mathcal{H} = \frac{m_a}{2} \sum_n \left(\frac{dx_n}{dt}\right)^2 + U, }[/math]

(1)

where the first term is the kinetic energy of the [math]\displaystyle{ n }[/math] atoms of mass [math]\displaystyle{ m_a }[/math], and the potential energy [math]\displaystyle{ U }[/math] is a sum of the potential energy due to the nearest-neighbor interaction and that of the substrate potential: [math]\displaystyle{ U = U_\text{sub} + U_\text{int} }[/math].

The substrate potential is periodic, i.e. [math]\displaystyle{ U_\text{sub}(x + a_s) = U_\text{sub}(x) }[/math] for some [math]\displaystyle{ a_s }[/math].

For non-harmonic interactions and/or non-sinusoidal potential, the FK model will give rise to a commensurate–incommensurate phase transition.

The FK model can be applied to any system that can be treated as two coupled sub-systems where one subsystem can be approximated as a linear chain and the second subsystem as a motionless substrate potential.

An example would be the adsorption of a layer onto a crystal surface, here the adsorption layer can be approximated as the chain, and the crystal surface as an on-site potential.

Classical model

In this section we examine in detail the simplest form of the FK model. A detailed version of this derivation can be found in the literature. The model describes a one-dimensional chain of atoms with a harmonic nearest neighbor interaction and subject to a sinusoidal potential. Transverse motion of the atoms is ignored, i.e. the atoms can only move along the chain. The Hamiltonian for this situation is given by 1, where we specify the interaction potential to be

[math]\displaystyle{ U_\text{int} = \frac{g}{2} \sum_n(x_{n+1} - x_n - a_0)^2, }[/math]

where [math]\displaystyle{ g }[/math] is the elastic constant, and [math]\displaystyle{ a_0 }[/math] is the inter-atomic equilibrium distance. The substrate potential is

[math]\displaystyle{ U_\text{sub} = \frac{\epsilon_s}{2} \sum_n \left[1 - \cos\frac{2\pi x_n}{a_s}\right], }[/math]

with [math]\displaystyle{ \epsilon_s }[/math] being the amplitude, and [math]\displaystyle{ a_s }[/math] the period.

The following dimensionless variables are introduced in order to rewrite the Hamiltonian:

[math]\displaystyle{ x_n \to \left(\frac{2\pi}{a_s}\right)x_{n}, \quad t \to \left(\frac{2\pi}{a_s}\right) \sqrt{\frac{\epsilon_s}{2m_a}} t, \quad a_0 \to \frac{2\pi}{a_s}, \quad g \to g \frac{a_s / 2\pi^2}{\epsilon_s / 2}. }[/math]

In dimensionless form the Hamiltonian is

[math]\displaystyle{ H = \frac{\mathcal{H}}{\epsilon_s / 2} = \sum_n \left[\frac{1}{2} \frac{dx_n}{dt}^2 + \left(1 - \cos x_n + \frac{1}{2} g(x_{n+1} - x_n - a_0)^2\right)\right], }[/math]

which describes a harmonic chain of atoms of unit mass in a sinusoidal potential of period [math]\displaystyle{ a_s = 2\pi }[/math] with amplitude [math]\displaystyle{ \epsilon_s = 2 }[/math]. The equation of motion for this Hamiltonian is

[math]\displaystyle{ \frac{d^2 x_n}{dt^2} + \sin x_n - g(x_{n+1} + x_{n-1} - 2x_n) = 0. }[/math]

We consider only the case where [math]\displaystyle{ a_0 }[/math] and [math]\displaystyle{ a_s }[/math] are commensurate, for simplicity we take [math]\displaystyle{ a_0 = a_s }[/math]. Thus in the ground state of the chain each minimum of the substrate potential is occupied by one atom. We introduce the variable [math]\displaystyle{ u_n }[/math] for atomic displacements which is defined by

[math]\displaystyle{ x_n = n a_s + u_n. }[/math]

For small displacements [math]\displaystyle{ u_n \ll a_s }[/math] the equation of motion may be linearized and takes the following form:

[math]\displaystyle{ \frac{d^2 u_n}{dt^2} + u_n - g(u_{n+1} + u_{n-1} - 2u_n) = 0. }[/math]

This equation of motion describes phonons with [math]\displaystyle{ u_n \propto \exp[i(\omega_{\text{ph}}(\kappa) t - \kappa n)] }[/math] with the phonon dispersion relation [math]\displaystyle{ \omega_{\text{ph}}^2(\kappa) = \omega_{\text{min}}^2 + 2g(1 - \cos \kappa) }[/math] with the dimensionless wavenumber [math]\displaystyle{ |\kappa| \leq \pi }[/math]. This shows that the frequency spectrum of the chain has a band gap [math]\displaystyle{ \omega_{\text{min}} \equiv \omega_\text{ph}(0) = 1 }[/math] with cut-off frequency [math]\displaystyle{ \omega_{\text{max}} \equiv \omega_\text{ph}(\pi) = \sqrt{\omega_{\text{min}}^2 + 4g} }[/math].

The linearised equation of motion are not valid when the atomic displacements are not small, and one must use the nonlinear equation of motion. The nonlinear equations can support new types of localized excitations, which are best illuminated by considering the continuum limit of the FK model. Applying the standard procedure of Rosenau to derive continuum-limit equations from a discrete lattice results in the perturbed sine-Gordon equation

[math]\displaystyle{ u_{tt} + \sin u - (a_s^2 g) u_{xx} = \epsilon f(u), }[/math]

where the function

[math]\displaystyle{ \epsilon f(u) = \frac{1}{12} a_s^2 (u_{xxtt} + u_x^2 \sin u - u_{xx} \cos u) }[/math]

describes in first order the effects due to the discreteness of the chain.

Neglecting the discreteness effects and introducing [math]\displaystyle{ x \to \frac{x}{a_s \sqrt{g}} }[/math] reduces the equation of motion to the sine-Gordon (SG) equation in its standard form

[math]\displaystyle{ u_{tt} - u_{xx} + \sin u = 0. }[/math]

The SG equation gives rise to three elementary excitations/solutions: kinks, breathers and phonons.

Kinks, or topological solitons, can be understood as the solution connecting two nearest identical minima of the periodic substrate potential, thus they are a result of the degeneracy of the ground state. These solutions are

[math]\displaystyle{ u_\text{k}(x, t) = 4 \tan^{-1}(\exp[-\sigma \gamma (v)(x - vt)]), }[/math]

where [math]\displaystyle{ \sigma = \pm 1 }[/math] is the topological charge. For [math]\displaystyle{ \sigma = 1 }[/math] the solution is called a kink, and for [math]\displaystyle{ \sigma = -1 }[/math] it is an antikink. The kink width [math]\displaystyle{ \gamma }[/math] is determined by the kink velocity [math]\displaystyle{ v }[/math], where [math]\displaystyle{ v }[/math] is measured in units of the sound velocity [math]\displaystyle{ c }[/math] and is [math]\displaystyle{ \gamma(v) = 1 / \sqrt{1 - v^2} }[/math]. For kink motion with [math]\displaystyle{ v^2 \ll c^2 }[/math], the width approximates 1. The energy of the kink in dimensionless units is

[math]\displaystyle{ E_\text{k} = mc^2 \gamma(v) \approx mc^2 + \frac{1}{2} mv^2, }[/math]

from which the rest mass of the kink follows as [math]\displaystyle{ m = \frac{2}{\pi^2 \sqrt{g}} }[/math], and the kinks rest energy as [math]\displaystyle{ \epsilon_\text{k} = mc^2 = 8 \sqrt{g} }[/math].

Two neighboring static kinks with distance [math]\displaystyle{ R }[/math] have energy of repulsion

[math]\displaystyle{ v_\text{int} \approx \epsilon_\text{k} \sinh^{-2} \frac{R}{2a_s \sqrt{g}}, }[/math]

whereas kink and antikink attract with interaction

[math]\displaystyle{ v_\text{int}(R) \approx -\epsilon_\text{k} \cosh^{-2} \frac{R}{2a_s \sqrt{g}}. }[/math]

A breather is

[math]\displaystyle{ u_\text{br}(x, t) = 4\tan^{-1}\left[\frac{\sqrt{1 - \Omega^2}}{\Omega} \frac{\sin(\Omega t)}{\cosh(x\sqrt{1 - \Omega^2})}\right], }[/math]

which describes nonlinear oscillation with frequency [math]\displaystyle{ \Omega }[/math], with [math]\displaystyle{ 0 \lt \Omega \lt \omega_\text{min} }[/math].

The breather rest energy

[math]\displaystyle{ \epsilon_\text{br} = 2 \epsilon_\text{k} \sqrt{1 - \Omega^2}. }[/math]

For low frequencies [math]\displaystyle{ \Omega \ll 1 }[/math] the breather can be seen as a coupled kink–antikink pair. Kinks and breathers can move along the chain without any dissipative energy loss. Furthermore, any collision between all the excitations of the SG equation result in only a phase shift. Thus kinks and breathers may be considered nonlinear quasi-particles of the SG model. For nearly integrable modifications of the SG equation such as the continuum approximation of the FK model kinks can be considered deformable quasi-particles, provided that discreetness effects are small.

The Peierls–Nabarro potential

Stationary configuration for the FK model for a single kink. Top image corresponds to a stable configuration. Bottom image corresponds to an unstable configuration.

In the preceding section the excitations of the FK model were derived by considering the model in a continuum-limit approximation. Since the properties of kinks are only modified slightly by the discreteness of the primary model, the SG equation can adequately describe most features and dynamics of the system.

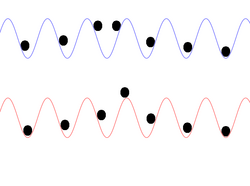
The discrete lattice does, however, influence the kink motion in a unique way with the existence of the Peierls–Nabarro (PN) potential [math]\displaystyle{ V_\text{PN}(X) }[/math], where [math]\displaystyle{ X }[/math] is the position of the kink's center. The existence of the PN potential is due to the lack of translational invariance in a discrete chain. In the continuum limit the system is invariant for any translation of the kink along the chain. For a discrete chain, only those translations that are an integer multiple of the lattice spacing [math]\displaystyle{ a_s }[/math] leave the system invariant. The PN barrier, [math]\displaystyle{ E_\text{PN} }[/math], is the smallest energy barrier for a kink to overcome so that it can move through the lattice. The value of the PN barrier is the difference between the kink's potential energy for a stable and unstable stationary configuration. The stationary configurations are shown schematically in the figure.