Physics:Crystal twinning

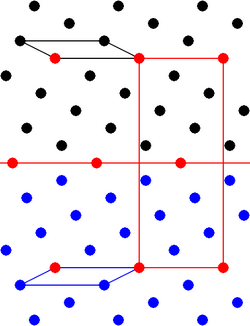
Crystal twinning occurs when two or more adjacent crystals of the same mineral are oriented so that they share some of the same crystal lattice points in a symmetrical manner. The result is an intergrowth of two separate crystals that are tightly bonded to each other. The surface along which the lattice points are shared in twinned crystals is called a composition surface or twin plane.
Crystallographers classify twinned crystals by a number of twin laws. These twin laws are specific to the crystal structure. The type of twinning can be a diagnostic tool in mineral identification.
Deformation twinning, in which twinning develops in a crystal in response to a shear stress, is an important mechanism for permanent shape changes in a crystal.[1]
Definition
Twinning is a form of symmetrical intergrowth between two or more adjacent crystals of the same mineral. It differs from the ordinary random intergrowth of mineral grains in a mineral deposit, because the relative orientations of the two crystal segments show a fixed relationship that is characteristic of the mineral structure. The relationship is defined by a symmetry operation called a twin operation.[2][3]
The twin operation is not one of the normal symmetry operations of the untwinned crystal structure. For example, the twin operation may be reflection across a plane that is not a symmetry plane of the single crystal.[2][3]
On the microscopic level, the twin boundary is characterized by a set of atomic positions in the crystal lattice that are shared between the two orientations.[2][3] These shared lattice points give the junction between the crystal segments much greater strength than that between randomly oriented grains, so that the twinned crystals do not easily break apart.[4]
Twin laws
Twin laws are symmetry operations that define the orientation between twin crystal segments. These are as characteristic of the mineral as are its crystal face angles. For example, crystals of staurolite show twinning at angles of almost precisely 90 degrees or 30 degrees.[4] A twin law is not a symmetry operation of the full set of basis points.[3]
Twin laws include reflection operations, rotation operations, and the inversion operation. Reflection twinning is described by the Miller indices of the twin plane (i.e. {hkl}) while rotational twinning is described by the direction of the twin axis (i.e. <hkl>). Inversion twinning is typically equivalent to a reflection or rotation symmetry.[2]
Rotational twin laws are almost always 2-fold rotations, though any other permitted rotation symmetry (3-fold, 4-fold, or 6-fold) is possible. The twin axis will be perpendicular to a lattice plane.[5] It is possible for a rotational twin law to share the same axis as a rotational symmetry of the individual crystal if the twin law is a 2-fold rotation and the symmetry operation is a 3-fold rotation. This is the case for spinel law twinning on <111>: The spinel structure has a 3-fold rotational symmetry on <111> and spinel is commonly twinned by 2-fold rotation on <111>.[2]
The boundary between crystal segments is called a composition surface or, if it is planar, a composition plane. The composition plane is often, though not always, parallel to the twin law plane of a reflection law. If this is the case, the twin plane is always parallel to a possible crystal face.[3]
Common twin laws
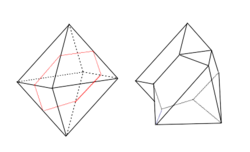
In the isometric system, the most common types of twins are the Spinel Law (twin plane, parallel to an octahedron) <111>, where the twin axis is perpendicular to an octahedral face, and the Iron Cross <001>, which is the interpenetration of two pyritohedrons, a subtype of dodecahedron.[6]
In the hexagonal system, calcite shows the contact twin laws {0001} and {0112}. Quartz shows the Brazil Law {1120}, and Dauphiné Law <0001>, which are penetration twins caused by transformation, and Japan Law {1122}, which is often caused by accidents during growth.[6]
In the tetragonal system, cyclical contact twins are the most commonly observed type of twin, such as in rutile titanium dioxide and cassiterite tin oxide.[6]
In the orthorhombic system, crystals usually twin on planes parallel to the prism face, where the most common is a {110} twin, which produces cyclical twins, such as in aragonite, chrysoberyl, and cerussite.[6]
In the monoclinic system, twins occur most often on the planes {100} and {001} by the Manebach Law {001}, Carlsbad Law [001], Braveno Law {021} in orthoclase, and the Swallow Tail Twins (Manebach law) {001} in gypsum.[6]
In the triclinic system, the most commonly twinned crystals are the feldspar minerals plagioclase and microcline. These minerals show the Albite and Pericline Laws.[5][6]
The most common twin operations by crystal system are tabulated below. This list is not exhaustive, particularly for the crystal systems of lowest symmetry, such as the triclinic system.[7][2][6]
| System | Law | Operation | Examples |
|---|---|---|---|
| Triclinic | Albite law Pericline law Carlsbad law Baveno law Manebach law |
{010} <010> <001> {021} {001} |
Plagioclase |
| Monoclinic | Carlsbad law Baveno law Manebach law |
<001> {021} {001} {100} <031> <231> |
Orthoclase Gypsum Staurolite |
| Orthorhombic | {110} {101} {011} |
Aragonite, cerrusite; often cyclic | |
| Tetragonal | {110} {101} {011} |
Cassiterite, rutile | |
| Hexagonal | Brazil law Dauphine law Japan law |
{0112} {0001} {1011} {1120} <0001> {1122} |
Calcite Quartz |
| Isometric | Spinel law Iron cross law |
<111> {111} {001} <001> |
Spinel Pyrite |
Types of twinning
Simple twinned crystals may be contact twins or penetration twins. Contact twins meet on a single composition plane, often appearing as mirror images across the boundary. Plagioclase, quartz, gypsum, and spinel often exhibit contact twinning.[4] Merohedral twinning occurs when the lattices of the contact twins superimpose in three dimensions, such as by relative rotation of one twin from the other.[8] An example is metazeunerite.[9] Contact twinning characteristically creates reentrant faces where faces of the crystal segments meet on the contact plane at an angle greater than 180°.[4]
A type of twinning involving 180° relationships is called hemitropism or hemitropy.
In penetration twins the individual crystals have the appearance of passing through each other in a symmetrical manner.[4] Orthoclase, staurolite, pyrite, and fluorite often show penetration twinning. The composition surface in penetration twins is usually irregular and extends to the center of the crystal.[3]
Contact twinning can arise from either reflection or rotation, whereas penetration twinning is usually produced by rotation.[3]
If several twin crystal parts are aligned by the same twin law they are referred to as multiple or repeated twins. If these multiple twins are aligned in parallel they are called polysynthetic twins. When the multiple twins are not parallel they are cyclic twins. Albite, calcite, and pyrite often show polysynthetic twinning. Closely spaced polysynthetic twinning is often observed as striations or fine parallel lines on the crystal face. Rutile, aragonite, cerussite, and chrysoberyl often exhibit cyclic twinning, typically in a radiating pattern.[4][3]
For rotational twinning the relationship between the twin axis and twin plane falls into one of three types:[10]
- parallel twinning, when the twin axis and compositional plane lie parallel to each other,
- normal twinning, when the twin plane and compositional plane lie normally, and
- complex twinning, a combination of parallel twinning and normal twinning on one compositional plane.
Modes of formation
There are three modes of formation of twinned crystals.
- Growth twins are the result of an interruption or change in the lattice during formation or growth due to a possible deformation from a larger substituting ion. Parallel growth describes a form of crystal growth that produces the appearance of a cluster of aligned crystals. Close examination reveals that the cluster is actually a single crystal. This is not twinning, since the crystal lattice is continuous throughout the cluster. Parallel growth likely takes place because it reduces system energy.[11]
- Annealing or transformation twins are the result of a change in crystal system during cooling as one form becomes unstable and the crystal structure must re-organize or transform into another more stable form.
- Deformation or gliding twins are the result of stress on the crystal after the crystal has formed. Because growth twins are formed during the initial growth of the crystal, they are described as primary, whereas transformation or deformation twins are formed in an existing crystal and are described as secondary.[12]
Growth twinning
Growth twinning likely begins early in crystal growth, since the contact surface usually passes through the center of the crystal. An atom joins a crystal face in a less than ideal position, forming a seed for growth of a twin. The original crystal and its twin then grow together and closely resemble each other. This is characteristic enough of certain minerals to suggest that it is thermodynamically or kinetically favored under conditions of rapid growth.[4][2] In certain materials cyclic twins such as that in the image can occur as they are lower in energy at small sizes.[13]
Transformation twinning
Transformation and annealing twinning takes place when a cooling crystal experiences a displacive polymorphic transition. For example, leucite has an isometric crystal structure above about 665 °C (1,229 °F), but becomes tetragonal below this temperature. Any one of the three original axes of a crystal can become the long axis when this phase change takes place. Twinning results when different parts of the crystal break their isometric symmetry along a different choice of axis. This is typically polysynthetic twinning, which enables the crystal to maintain its isometric shape by averaging out the displacement in each direction. This produces a pseudomorphic crystal that appears to have isometric symmetry. Potassium feldspar likewise experiences polysynthetic twinning as it transforms from a monoclinic structure (orthoclase) to a triclinic structure (microcline) on slow cooling.[2]
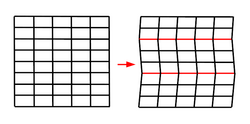
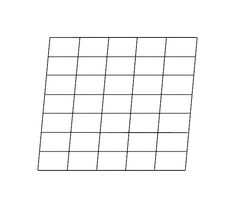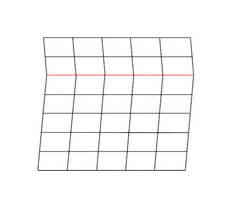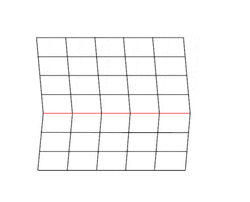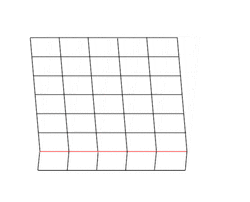
Deformation twinning
Deformation twinning is a response to shear stress. The crystal structure is displaced along successive planes of the crystal, a process also called glide. The twinning is always reflection twinning and the glide plane is also the mirror plane. Deformation twinning can be observed in a calcite cleavage fragment by applying gentle pressure with a knife blade near an edge. This particular glide twinning, {102}, is found almost universally in deformed rock beds containing calcite.[2]
Twinning and slip are competitive mechanisms for crystal deformation. Each mechanism is dominant in certain crystal systems and under certain conditions.[14] In fcc metals, slip is almost always dominant because the stress required is far less than twinning stress.[15]
Twinning can occur by cooperative displacement of atoms along the face of the twin boundary. This displacement of a large quantity of atoms simultaneously requires significant energy to perform. Therefore, the theoretical stress required to form a twin is quite high. It is believed that twinning is associated with dislocation motion on a coordinated scale, in contrast to slip, which is caused by independent glide at several locations in the crystal.
Compared to slip, twinning produces a deformation pattern that is more heterogeneous in nature. This deformation produces a local gradient across the material and near intersections between twins and grain boundaries. The deformation gradient can lead to fracture along the boundaries, particularly in bcc transition metals at low temperatures.
Of the three common crystalline structures bcc, fcc, and hcp, the hcp structure is the most likely to form deformation twins when strained, because they rarely have a sufficient number of slip systems for an arbitrary shape change. High strain rates, low stacking-fault energy and low temperatures facilitate deformation twinning.[1]
If a metal with face-centered cubic (fcc) structure, like Al, Cu, Ag, Au, etc., is subjected to stress, it will experience twinning. The formation and migration of twin boundaries is partly responsible for ductility and malleability of fcc metals.[16]
Twin boundaries are partly responsible for shock hardening and for many of the changes that occur in cold work of metals with limited slip systems or at very low temperatures. They also occur due to martensitic transformations: the motion of twin boundaries is responsible for the pseudoelastic and shape-memory behavior of nitinol, and their presence is partly responsible for the hardness due to quenching of steel. In certain types of high strength steels, very fine deformation twins act as primary obstacles against dislocation motion. These steels are referred to as 'TWIP' steels, where TWIP stands for twinning-induced plasticity.[17]
Deformation twinning crystallography
Twinning is crystallographically defined by its twin plane 𝑲𝟏, the mirror plane in the twin and parent material, and 𝜼𝟏, which is the twinning shear direction. Deformation twins in Zr are generally lenticular in shape, lengthening in the 𝜼𝟏 direction and thickening along the 𝑲𝟏 plane normal.[18]
The twin plane, shear direction, and shear plane form the basis vectors of an orthogonal set. The axis-angle misorientation relationship between the parent and twin is a rotation of angle 𝜉 about the shear plane's normal direction 𝑷.
More generally, twinning can be described as a 180° rotation about an axis (𝑲𝟏 for type I twins or 𝜼𝟏 for type II twins normal direction) , or a mirror reflection in a plane (𝑲𝟏 or 𝜼𝟏 normal plane).[19]
In addition to a homogeneous shear, atomic shuffles are sometimes required to reform the correct crystal structure in the twinned lattice. For each twin variant, a reciprocal twin with swapped 𝑲𝟏 and 𝑲2, 𝜼𝟏 and 𝜼2 is possible, but one variant may appear more frequently in reality due to complexities with the required shuffles.[20]
there are only two crystallographic planes in a shearing action that do not change their shape and size as a consequence of the shear. The first 𝑲𝟏 is the plane defining the upper and lower surfaces of the sheared volume. This plane contains the shear direction. The other plane, designated C. The shear direction is shown with an arrow and labelled with its customary designation 𝜼𝟏. It follows from the above that there are three ways that a crystal lattice can be sheared while still retaining its crystal structure and symmetry:
- When 𝑲𝟏 is a rational plane and 𝜼2 a rational direction, a twin of the first kind
- When 𝑲2 is a rational plane and 𝜼𝟏 a rational direction, a twin of the second kind, rare
- When all four elements 𝑲𝟏, 𝑲2, 𝜼𝟏, and 𝜼2 are rational, a compound twin
Deformation twinning configuration
A deformation twin embryo forms in BCC metal by accumulating stacking faults, with a variant selection governed by the local stress state.[21][22][23] Variation of the stress field close to twins inferred from HR-EBSD experimental[24][25] and crystal plasticity finite element (CPFE) simulation data indicated that twins nucleate on sites with maximum strain energy density and twin resolved shear stress; thus, reducing the total elastic energy after formation. This relaxation depends on the twin thickness and is a deciding factor in the spacing between twins.[26] Experimental[27] and three-dimensional[28] analysis has focussed on the (stored) strain energy density measured along a path. This highly localised stress field can provide a sufficient driving force for concurrent twin nucleation[29] and inter/intra-granular crack nucleation.
Deformation twin growth can be perceived as a two-step process of i) thickening that is mediated by the interaction between the residual and mobile twin partials at the coherent twin-parent interface,[30] and ii) dislocation mobility along the twin shear direction.[31] The twin propagates when the homogeneous shear stress reaches a critical value, and a twin-parent interface advances inside the parent grain [240]. The propagating deformation twin generates a stress field due to its confinement by the surrounding parent crystal, and deformation twins develop a 3D oblate spheroid shape (which appears in 2D sections as a bi-convex lens) with a mixed coherent and non-coherent interface (Figure b).[31]
Kannan et al.[32] found, using in-situ ultra-high-speed optical imaging, that twin nucleation in single-crystal magnesium is stress-driven accompanied by instantaneous propagation at a speed of 1 km/s (initially) that prioritises volume lateral thickening over forward propagation, past a critical width where growth is then become faster along the shear direction. Barnett[33] also indicated that growth is due to twin tip extension. Furthermore, elastic simulations of the local stress field surrounding the ellipsoidal twin tip find that the field can be described using its lens angle ([math]\displaystyle{ \beta }[/math]) and that the stress field magnitude increases with twin thickness.[34]
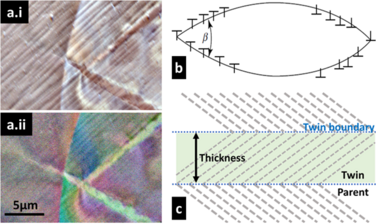
In practice, plastic accommodation occurs in the parent crystal; thus, it also depends on the material’s yield stress, the anisotropic elastic stiffness of the parent crystal lattice, and the deformation twinning shear magnitude.[30] This can also be accompanied by long-range diffusion of elements and elemental segregation (e.g., Cr and Co in single crystal Ni-based superalloy MD2), which occurs at the twin boundary to facilitate twin growth by lowering the critical stacking fault energy.[36] A linear variation has been observed between twin thickness, stacking fault energy and grain size,[37] and to a lesser degree, the stress state of the twinning grain (Schmid Factor).[38] The twin thickness saturated once a critical residual dislocations’ density reached the coherent twin-parent crystal boundary.[23][39]
Significant attention has been paid to the crystallography,[40] morphology[41] and macro mechanical effects[42] of deformation twinning. Although the criterion for deformation twin growth is not entirely understood, it is a tip-controlled phenomenon linked to the interaction between the residual and mobile twin partials at the twin interface; thermodynamically, this involves the elastic energy of the strained lattice, the interface and volume free-energy of the twin, and the dissipated energy of the growth mechanism.[43] To fully understand the interactions between microstructure (i.e., grain size, texture), temperature and strain rate on deformation twinning, it is crucial to characterise the (high) local stress and strain field associated with twin thickening and propagation. This is especially important for materials where cleavage fracture can be initiated by twinning (e.g., iron-silicon, the ferrite phase of age-hardened duplex stainless-steel, and single-crystal magnesium) as a stress-relieving mechanism.
Early studies of deformation twins arrested within grains of niobium[44] and iron[45] visualised the highly local strain concentration at the twin tip using an etch-pit procedure. More recently, high-resolution electron backscatter diffraction (HR-EBSD) has been used to investigate the strain 'singularity' ahead of a twin tip in hexagonal close-packed (HCP) zirconium alloy. A deformation twin in commercial purity titanium was characterised similarly and then quantified using a local Schmid factor (LSF) at the twin tip,[46] as described in equation below.
[math]\displaystyle{ \mathrm{LSF} = \frac{\boldsymbol{\sigma} : \boldsymbol{P}^i}{\|\boldsymbol{\sigma}\|}, \quad \boldsymbol{S}^i = \boldsymbol{d}^i \otimes \mathbf{n}^i }[/math]
where σ is the stress tensor, Si is the Schmid tensor, Pi is its symmetric part, di is the shear direction and ni is the shear plane normal for ith slip system. The authors concluded that conditions at the twin tip control thickening and propagation in a manner analogous to the operation of dislocation sources ahead of a crack-tip.[47] In the analysis, a broad region of high LSF ahead of the twin tip favoured propagation, whereas a narrow region of high LSF promoted thickening. Since then, it has been argued[48] that the LSF firmly controls the twin variant selection, as twinning has strong polarity.
The LSF novelty – compared to other criteria to describe conditions at the twin[37] – lies in combining a geometrical criterion with the deformation field in the parent grain to provide an approximate indication of the local twin mode (i.e., thickening or propagation). However, the LSF analysis does not take advantage of the available full-field data, relies on global information on the applied stress, and does not consider the energy balance that drives twin growth. There have been few in-situ experiments to quantify the strain field ahead of a propagating deformation twin.[35][25] Such observations might validate geometrical or hybrid geometrical-energy-based criteria[48] for growth. Nanoscale testing (i.e., transmission electron microscopy) may not represent the behaviour in bulk samples due to plasticity starvation, i.e., large surface area to volume ratio,[49] so a suitable analysis method is needed.
Lloyd[39] described the stress concentration field ahead of the twin tip using a two-dimensional dislocation-based model within a single magnesium grain. Wang and Li,[50] who considered microscopic phase-field (MPF) models of cracks, noted that the stress fields were similar for dislocations, deformation twinning and martensitic transformations, with differences only in the traction of the created surface, i.e., there is 100% traction recovery for dislocations and a traction-free surface for a crack. They highlighted that the stress field singularity regulates the advancement of the crack-tip and dislocations. This stress concentration can be characterised using a path-independent line integral, as shown by Eshelby for dislocations considering the contribution from the surface traction and ellipsoidal inclusions,[51] and Rice[52] for cracks and stress concentrations with traction-free surfaces. Furthermore, Venables[53] noted that the oblate spheroid shape of the twin tip is the ideal example of an ellipsoid inclusion or a notch.
See also
- Macle
- Tin cry
- Icosahedral twins
- Slip bands
- Slip (materials science)
References
- ↑ 1.0 1.1 Courtney, Thomas H. (2000) Mechanical Behavior of Materials, 2nd ed. McGraw Hill. ISBN:1-57766-425-6
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 Nesse, William D. (2000). Introduction to mineralogy. New York: Oxford University Press. pp. 87–91. ISBN 9780195106916.
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 3.6 3.7 Klein, Cornelis; Hurlbut, Cornelius S. Jr. (1993). Manual of mineralogy : (after James D. Dana) (21st ed.). New York: Wiley. pp. 102–106. ISBN 047157452X.
- ↑ 4.0 4.1 4.2 4.3 4.4 4.5 4.6 4.7 Sinkankas, John (1964). Mineralogy for amateurs.. Princeton, N.J.: Van Nostrand. pp. 96–105. ISBN 0442276249.
- ↑ 5.0 5.1 Nelson, Stephen A. (2013). "Twinning, Polymorphism, Polytypism, Pseudomorphism". Tulane University. https://www.tulane.edu/~sanelson/eens211/twinning.htm.
- ↑ 6.0 6.1 6.2 6.3 6.4 6.5 6.6 Klein & Hurlbut 1993, pp. 104–106.
- ↑ Nesse 2000, pp. 89, 214–216.
- ↑ Yeates, Todd O. (1997). "[22] Detecting and overcoming crystal twinning". Macromolecular Crystallography Part A. Methods in Enzymology. 276. pp. 344–358. doi:10.1016/S0076-6879(97)76068-3. ISBN 9780121821777.
- ↑ Locock, A. J.; Burns, P. C. (1 April 2003). "Crystal Structures and Synthesis of the Copper-Dominant Members of the Autunite and Meta-Autunite Groups: Torbernite, Zeunerite, Metatorbernite and Metazeunerite". The Canadian Mineralogist 41 (2): 489–502. doi:10.2113/gscanmin.41.2.489. Bibcode: 2003CaMin..41..489L.
- ↑ Tobi, Alexander C. (1961). "The recognition of plagioclase twins in sections normal to the composition plane". American Mineralogist 46 (11–12): 1470–1488. https://pubs.geoscienceworld.org/msa/ammin/article-abstract/46/11-12/1470/541849/The-recognition-of-plagioclase-twins-in-sections. Retrieved 19 February 2022.
- ↑ Klein & Hurlbut 1993, p. 101.
- ↑ Klein & Hurlbut 1993, p. 167.
- ↑ Marks, Laurence. D. (2023), Shape, thermodynamics and kinetics of nanoparticles, Elsevier, pp. 383–417, doi:10.1016/b978-0-12-822425-0.00082-8, ISBN 978-0-12-822423-6, http://dx.doi.org/10.1016/b978-0-12-822425-0.00082-8, retrieved 2023-07-11
- ↑ Mahajan, S.; Williams, D. F. (June 1973). "Deformation Twinning in Metals and Alloys". International Metallurgical Reviews 18 (2): 43–61. doi:10.1179/imtlr.1973.18.2.43.
- ↑ Beyerlein, Irene J.; Mara, Nathan A.; Bhattacharyya, Dhriti; Alexander, David J.; Necker, Carl T. (January 2011). "Texture evolution via combined slip and deformation twinning in rolled silver–copper cast eutectic nanocomposite". International Journal of Plasticity 27 (1): 121–146. doi:10.1016/j.ijplas.2010.05.007.
- ↑ Nurul Akmal Che, Lah; Trigueros, Sonia (2019). "Synthesis and modelling of the mechanical properties of Ag, Au and Cu nanowires". Sci. Technol. Adv. Mater. 20 (1): 225–261. doi:10.1080/14686996.2019.1585145. PMID 30956731. Bibcode: 2019STAdM..20..225L.
- ↑ Steinmetz, D.R.; Jäpel, T.; Wietbrock, B.; Eisenlohr, P.; Gutierrez-Urrutia, I.; Saeed (2013), "Revealing the strain-hardening behavior of twinning-induced plasticity steels: Theory, simulations, experiments", Acta Materialia 61 (2): 494, doi:10.1016/j.actamat.2012.09.064, Bibcode: 2013AcMat..61..494S.
- ↑ Christian, J.W.; Mahajan, S. (1995). "Deformation twinning" (in en). Progress in Materials Science 39 (1–2): 1–157. doi:10.1016/0079-6425(94)00007-7. https://linkinghub.elsevier.com/retrieve/pii/0079642594000077.
- ↑ Calhoun, C.A.; Garlea, E.; Sisneros, T.A.; Agnew, S.R. (April 2018). "In-situ neutron diffraction characterization of temperature dependence deformation in α-uranium" (in en). Journal of Nuclear Materials 502: 60–67. doi:10.1016/j.jnucmat.2018.01.036. Bibcode: 2018JNuM..502...60C.
- ↑ Bilby, B. A.; Crocker, A. G. (1965-10-26). "The theory of the crystallography of deformation twinning" (in en). Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences 288 (1413): 240–255. doi:10.1098/rspa.1965.0216. ISSN 0080-4630. Bibcode: 1965RSPSA.288..240B. https://royalsocietypublishing.org/doi/10.1098/rspa.1965.0216.
- ↑ Cahn, R.W. (Oct 1954). "Twinned crystals" (in en). Advances in Physics 3 (12): 363–445. doi:10.1080/00018735400101223. ISSN 0001-8732. Bibcode: 1954AdPhy...3..363C.
- ↑ Wang, S.; Schuman, C.; Bao, L.; Lecomte, J.S.; Zhang, Y.; Raulot, J.M.; Philippe, M.J.; Zhao, X. et al. (May 2012). "Variant selection criterion for twin variants in titanium alloys deformed by rolling" (in en). Acta Materialia 60 (9): 3912–3919. doi:10.1016/j.actamat.2012.03.046. Bibcode: 2012AcMat..60.3912W. https://hal-cnrs.archives-ouvertes.fr/hal-03864487/file/rolling%20version2.pdf.
- ↑ 23.0 23.1 Christian, J.W. (2002). "Deformation Twinning" (in en). The Theory of Transformations in Metals and Alloys. Elsevier. pp. 859–960. doi:10.1016/b978-008044019-4/50025-8. ISBN 978-0-08-044019-4.
- ↑ Abdolvand, Hamidreza; Sedaghat, Omid; Guo, Yi (Oct 2018). "Nucleation and growth of { 1122 } twins in titanium: Elastic energy and stress fields at the vicinity of twins" (in en). Materialia 2: 58–62. doi:10.1016/j.mtla.2018.06.012.
- ↑ 25.0 25.1 Guo, Y.; Schwiedrzik, J.; Michler, J.; Maeder, X. (2016-11-01). "On the nucleation and growth of {112¯2} twin in commercial purity titanium: In situ investigation of the local stress field and dislocation density distribution" (in en). Acta Materialia 120: 292–301. doi:10.1016/j.actamat.2016.08.073. ISSN 1359-6454.
- ↑ Paudel, YubRaj; Barrett, Christopher D.; Tschopp, Mark A.; Inal, Kaan; El Kadiri, Haitham (July 2017). "Beyond initial twin nucleation in hcp metals: Micromechanical formulation for determining twin spacing during deformation" (in en). Acta Materialia 133: 134–146. doi:10.1016/j.actamat.2017.05.013. ISSN 1359-6454. Bibcode: 2017AcMat.133..134P.
- ↑ Paramatmuni, Chaitanya; Zheng, Zebang; Rainforth, W. Mark; Dunne, Fionn P. E. (2020-12-01). "Twin nucleation and variant selection in Mg alloys: An integrated crystal plasticity modelling and experimental approach" (in en). International Journal of Plasticity 135: 102778. doi:10.1016/j.ijplas.2020.102778. ISSN 0749-6419. https://eprints.whiterose.ac.uk/171770/3/WE43_twin_nucleation_paper.pdf.
- ↑ Paramatmuni, Chaitanya; Guo, Yi; Withers, Philip J.; Dunne, Fionn P. E. (2021-08-01). "A three-dimensional mechanistic study of the drivers of classical twin nucleation and variant selection in Mg alloys: A mesoscale modelling and experimental study" (in en). International Journal of Plasticity 143: 103027. doi:10.1016/j.ijplas.2021.103027. ISSN 0749-6419.
- ↑ Arul Kumar, M.; Beyerlein, I. J.; Tomé, C. N. (2016-09-01). "Effect of local stress fields on twin characteristics in HCP metals" (in en). Acta Materialia 116: 143–154. doi:10.1016/j.actamat.2016.06.042. ISSN 1359-6454. Bibcode: 2016AcMat.116..143A.
- ↑ 30.0 30.1 Beyerlein, Irene J.; Zhang, Xinghang; Misra, Amit (July 2014). "Growth Twins and Deformation Twins in Metals" (in en). Annual Review of Materials Research 44 (1): 329–363. doi:10.1146/annurev-matsci-070813-113304. ISSN 1531-7331. Bibcode: 2014AnRMS..44..329B.
- ↑ 31.0 31.1 Britton, T. B.; Dunne, F. P. E.; Wilkinson, A. J. (2015-06-08). "On the mechanistic basis of deformation at the microscale in hexagonal close-packed metals". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 471 (2178): 20140881. doi:10.1098/rspa.2014.0881. Bibcode: 2015RSPSA.47140881B.
- ↑ Liu, Y.; Tang, P. Z.; Gong, M. Y.; McCabe, R. J.; Wang, J.; Tomé, C. N. (2019-07-25). "Three-dimensional character of the deformation twin in magnesium" (in en). Nature Communications 10 (1): 3308. doi:10.1038/s41467-019-10573-7. ISSN 2041-1723. PMID 31346160. Bibcode: 2019NatCo..10.3308L.
- ↑ Barnett, M. R. (2007-08-25). "Twinning and the ductility of magnesium alloys: Part I: "Tension" twins" (in en). Materials Science and Engineering: A 464 (1): 1–7. doi:10.1016/j.msea.2006.12.037. ISSN 0921-5093.
- ↑ Arul Kumar, M.; Kanjarla, A. K.; Niezgoda, S. R.; Lebensohn, R. A.; Tomé, C. N. (2015-02-01). "Numerical study of the stress state of a deformation twin in magnesium" (in en). Acta Materialia 84: 349–358. doi:10.1016/j.actamat.2014.10.048. ISSN 1359-6454.
- ↑ 35.0 35.1 Koko, Abdalrhaman; Elmukashfi, Elsiddig; Dragnevski, Kalin; Wilkinson, Angus J.; Marrow, Thomas James (2021-10-01). "J-integral analysis of the elastic strain fields of ferrite deformation twins using electron backscatter diffraction" (in en). Acta Materialia 218: 117203. doi:10.1016/j.actamat.2021.117203. ISSN 1359-6454. Bibcode: 2021AcMat.21817203K. https://ora.ox.ac.uk/objects/uuid:4071edea-3bfc-4d2b-8d32-c3b05bd73372.
- ↑ Barba, D.; Alabort, E.; Pedrazzini, S.; Collins, D. M.; Wilkinson, A. J.; Bagot, P. A. J.; Moody, M. P.; Atkinson, C. et al. (2017-08-15). "On the microtwinning mechanism in a single crystal superalloy" (in en). Acta Materialia 135: 314–329. doi:10.1016/j.actamat.2017.05.072. ISSN 1359-6454. Bibcode: 2017AcMat.135..314B.
- ↑ 37.0 37.1 Mahajan, S.; Williams, D. F. (1973-06-01). "Deformation Twinning in Metals and Alloys". International Metallurgical Reviews 18 (2): 43–61. doi:10.1179/imtlr.1973.18.2.43. ISSN 0367-9020.
- ↑ Beyerlein, I.J.; Capolungo, L.; Marshall, P.E.; McCabe, R.J.; Tomé, C.N. (2010-05-28). "Statistical analyses of deformation twinning in magnesium" (in en). Philosophical Magazine 90 (16): 2161–2190. doi:10.1080/14786431003630835. ISSN 1478-6435. Bibcode: 2010PMag...90.2161B.
- ↑ 39.0 39.1 Lloyd, J. T. (2018-02-28). "A dislocation-based model for twin growth within and across grains". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 474 (2210): 20170709. doi:10.1098/rspa.2017.0709. PMID 29507516. Bibcode: 2018RSPSA.47470709L.
- ↑ Venables, J. A. (1961-03-01). "Deformation twinning in face-centred cubic metals". The Philosophical Magazine 6 (63): 379–396. doi:10.1080/14786436108235892. ISSN 0031-8086. Bibcode: 1961PMag....6..379V.
- ↑ Johansson, Johan; Odén, Magnus (2000-06-01). "Load sharing between austenite and ferrite in a duplex stainless steel during cyclic loading" (in en). Metallurgical and Materials Transactions A 31 (6): 1557–1570. doi:10.1007/s11661-000-0166-3. ISSN 1543-1940.
- ↑ Marrow, T. J.; King, J. E. (1994-06-15). "Fatigue crack propagation mechanisms in a thermally aged duplex stainless steel" (in en). Materials Science and Engineering: A 183 (1): 91–101. doi:10.1016/0921-5093(94)90893-1. ISSN 0921-5093.
- ↑ Christian, J. W.; Mahajan, S. (1995-01-01). "Deformation twinning" (in en). Progress in Materials Science 39 (1): 1–157. doi:10.1016/0079-6425(94)00007-7. ISSN 0079-6425.
- ↑ Sleeswyk, A. W (1962-08-01). "Emissary dislocations: Theory and experiments on the propagation of deformation twins in α-iron" (in en). Acta Metallurgica 10 (8): 705–725. doi:10.1016/0001-6160(62)90040-8. ISSN 0001-6160.
- ↑ Spreadborough, J.; Langheinrich, D.; Anderson, E.; Brandon, D. (Dec 1964). "Etch-Pit Observations Concerning Twins in Iron and Iron Alloys" (in en). Journal of Applied Physics 35 (12): 3585–3587. doi:10.1063/1.1713275. ISSN 0021-8979. Bibcode: 1964JAP....35.3585S.
- ↑ Guo, Y.; Abdolvand, H.; Britton, T. B.; Wilkinson, A. J. (2017-03-01). "Growth of {1122} twins in titanium: A combined experimental and modelling investigation of the local state of deformation" (in en). Acta Materialia 126: 221–235. doi:10.1016/j.actamat.2016.12.066. ISSN 1359-6454.
- ↑ Baxevanakis, K. P.; Gourgiotis, P. A.; Georgiadis, H. G. (July 2017). "Interaction of cracks with dislocations in couple-stress elasticity. Part I: Opening mode" (in en). International Journal of Solids and Structures 118-119: 179–191. doi:10.1016/j.ijsolstr.2017.03.019. ISSN 0020-7683.
- ↑ 48.0 48.1 Kacher, Josh; Sabisch, Julian E.; Minor, Andrew M. (2019-07-01). "Statistical analysis of twin/grain boundary interactions in pure rhenium" (in en). Acta Materialia 173: 44–51. doi:10.1016/j.actamat.2019.04.051. ISSN 1359-6454. Bibcode: 2019AcMat.173...44K.
- ↑ Gong, Mingyu; Hirth, John P.; Liu, Yue; Shen, Yao; Wang, Jian (2017-11-03). "Interface structures and twinning mechanisms of twins in hexagonal metals". Materials Research Letters 5 (7): 449–464. doi:10.1080/21663831.2017.1336496.
- ↑ Wang, Yunzhi; Li, Ju (2010-02-01). "Phase field modeling of defects and deformation" (in en). Acta Materialia 58 (4): 1212–1235. doi:10.1016/j.actamat.2009.10.041. ISSN 1359-6454. Bibcode: 2010AcMat..58.1212W.
- ↑ Eshelby, John Douglas; Mott, Nevill Francis (1951-11-06). "The force on an elastic singularity". Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences 244 (877): 87–112. doi:10.1098/rsta.1951.0016. Bibcode: 1951RSPTA.244...87E. https://royalsocietypublishing.org/doi/10.1098/rsta.1951.0016.
- ↑ Rice, J. R. (1968-06-01). "A Path Independent Integral and the Approximate Analysis of Strain Concentration by Notches and Cracks" (in en). Journal of Applied Mechanics 35 (2): 379–386. doi:10.1115/1.3601206. ISSN 0021-8936. Bibcode: 1968JAM....35..379R. https://asmedigitalcollection.asme.org/appliedmechanics/article/35/2/379/392117/A-Path-Independent-Integral-and-the-Approximate.
- ↑ Venables, J. A (1964-07-01). "The electron microscopy of deformation twinning" (in en). Journal of Physics and Chemistry of Solids 25 (7): 685–692. doi:10.1016/0022-3697(64)90177-5. ISSN 0022-3697. Bibcode: 1964JPCS...25..685V.
External links
- Slip and twinning mechanism in detail
- Mineral galleries – twins
- Mathematical and Theoretical Crystallography
- Quartz Crystals – Twinning
- Grain Boundary Twinning
 |