Physics:Charge-transfer insulators
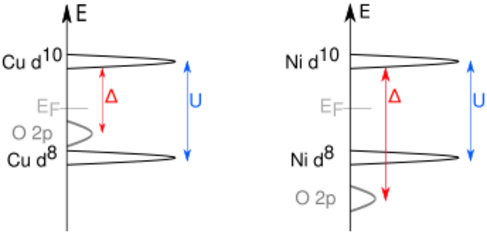
Charge-transfer insulators are a class of materials predicted to be conductors following conventional band theory, but which are in fact insulators due to a charge-transfer process. Unlike in Mott insulators, where the insulating properties arise from electrons hopping between unit cells, the electrons in charge-transfer insulators move between atoms within the unit cell. In the Mott–Hubbard case, it's easier for electrons to transfer between two adjacent metal sites (on-site Coulomb interaction U); here we have an excitation corresponding to the Coulomb energy U with
[math]\displaystyle{ d^nd^n \rightarrow d^{n-1}d^{n+1}, \quad \Delta E = U = U_{dd} }[/math].
In the charge-transfer case, the excitation happens from the anion (e.g., oxygen) p level to the metal d level with the charge-transfer energy Δ:
[math]\displaystyle{ d^np^6 \rightarrow d^{n+1}p^{5}, \quad \Delta E = \Delta_{CT} }[/math].
U is determined by repulsive/exchange effects between the cation valence electrons. Δ is tuned by the chemistry between the cation and anion. One important difference is the creation of an oxygen p hole, corresponding to the change from a 'normal' [math]\ce{ O^2- }[/math] to the ionic [math]\ce{ O- }[/math] state.[1] In this case the ligand hole is often denoted as [math]\displaystyle{ \underline{L} }[/math].
Distinguishing between Mott-Hubbard and charge-transfer insulators can be done using the Zaanen-Sawatzky-Allen (ZSA) scheme.[2]
Exchange interaction
Analogous to Mott insulators we also have to consider superexchange in charge-transfer insulators. One contribution is similar to the Mott case: the hopping of a d electron from one transition metal site to another and then back the same way. This process can be written as
[math]\displaystyle{ d^n_ip^6d^n_j \rightarrow d^n_ip^5d^{n+1}_j \rightarrow d^{n-1}_ip^6d^{n+1}_j \rightarrow d^n_ip^5d^{n+1}_j \rightarrow d^n_ip^6d^n_j }[/math].
This will result in an antiferromagnetic exchange (for nondegenerate d levels) with an exchange constant [math]\displaystyle{ J = J_{dd} }[/math].
[math]\displaystyle{ J_{dd} = \frac{2t^2_{dd}}{U_{dd}} = \cfrac{2t^4_{pd}}{\Delta_{CT}^2U_{dd}} }[/math]
In the charge-transfer insulator case
[math]\displaystyle{ d^n_i p^6d^n_j \rightarrow d^n_i p^5d^{n+1}_j \rightarrow d^{n+1}_i p^4d^{n+1}_j \rightarrow d^{n+1}_i p^5d^n_j \rightarrow d^n_i p^6d^n_j }[/math].
This process also yields an antiferromagnetic exchange [math]\displaystyle{ J_{pd} }[/math]:
[math]\displaystyle{ J_{pd} = \cfrac{4t^4_{pd}}{\Delta^2_{CT}\cdot\left(2\Delta_{CT}+U_{pp}\right)} }[/math]
The difference between these two possibilities is the intermediate state, which has one ligand hole for the first exchange ([math]\displaystyle{ p^6\rightarrow p^5 }[/math]) and two for the second ([math]\displaystyle{ p^6\rightarrow p^4 }[/math]).
The total exchange energy is the sum of both contributions:
[math]\displaystyle{ J_{total} = \cfrac{2t^4_{pd}}{\Delta^2_{CT}} \cdot \left(\cfrac{1}{U_{dd}} + \cfrac{1}{\Delta_{CT} + \tfrac{1}{2}U_{pp}}\right) }[/math].
Depending on the ratio of [math]\displaystyle{ U_{dd}\text{ and } \left(\Delta_{CT}+\tfrac{1}{2}U_{pp}\right) }[/math], the process is dominated by one of the terms and thus the resulting state is either Mott-Hubbard or charge-transfer insulating.[1]
References
- ↑ 1.0 1.1 Khomskii, Daniel I. (2014). Transition Metal Compounds. Cambridge: Cambridge University Press. doi:10.1017/cbo9781139096782. ISBN 978-1-107-02017-7. https://www.cambridge.org/core/books/transition-metal-compounds/037907D3274F602D84CFECA02A493395.
- ↑ Zaanen, J.; Sawatzky, G. A.; Allen, J. W. (1985-07-22). "Band gaps and electronic structure of transition-metal compounds". Physical Review Letters 55 (4): 418–421. doi:10.1103/PhysRevLett.55.418. PMID 10032345. Bibcode: 1985PhRvL..55..418Z. https://link.aps.org/doi/10.1103/PhysRevLett.55.418.
 |