Physics:Relative wind stress
Relative wind stress is a shear stress that is produced by wind blowing over the surface of the ocean, or another large body of water. Relative wind stress is related to wind stress but takes the difference between the surface ocean current velocity and wind velocity into account. The units are Newton per meter squared [math]\displaystyle{ [Nm^{-2}] }[/math] or Pascal [math]\displaystyle{ [Pa] }[/math]. Wind stress over the ocean is important as it is a major source of kinetic energy input to the ocean which in turn drives large scale ocean circulation.[1] The use of relative wind stress instead of wind stress, where the ocean current is assumed to be stationary, reduces the stress felt over the ocean in models. This leads to a decrease in the calculation of power input into the ocean of 20–35% and thus, results in a different simulation of the large scale ocean circulation.[2]

Mathematical formulation
The wind stress [math]\displaystyle{ (\tau) }[/math] acting on the ocean surface is usually parameterized using the turbulent drag formula
[math]\displaystyle{ \quad \tau = C_d \rho_{a} |\vec{u}_{a}| \vec{u}_{a} }[/math].
where [math]\displaystyle{ C_d }[/math] is the turbulent drag coefficient (usually determined empirically), [math]\displaystyle{ \rho_{a} }[/math] is the air density, and [math]\displaystyle{ \vec{u}_{a} }[/math] is the wind velocity vector, usually taken at 10m above sea level. This parameterization is commonly referred to as resting ocean approximation.[3] From now on we will refer to wind stress in resting ocean approximation as simply resting ocean wind stress.
On the other hand, relative wind stress [math]\displaystyle{ (\tau_{rel}) }[/math] makes use of the velocity of the surface wind relative to the velocity at the ocean surface [math]\displaystyle{ \vec{u}_{o} }[/math], as follows,
[math]\displaystyle{ \quad \tau_{rel} = C_d \rho_{a} |\vec{u}_{a}-\vec{u}_{o}| (\vec{u}_{a}-\vec{u}_{o}) }[/math].
where [math]\displaystyle{ \vec{u}_{o} }[/math] is the surface ocean velocity and thus, the terms with [math]\displaystyle{ (\vec{u}_a - \vec{u}_o) }[/math] represent the wind velocity relative to the surface ocean velocity.[4][5] Therefore, the difference between wind stress and relative wind stress is that relative wind stress takes into account the relative motion of the wind with respect to the surface ocean current.
Work done by the wind on the ocean
The work wind does on the ocean can be computed by
[math]\displaystyle{ \qquad P= \tau \cdot \vec{u}_{o} }[/math]
where [math]\displaystyle{ \tau }[/math] is the chosen parameterization for the wind stress.
Thus, in resting ocean approximation, the work done on the ocean by the wind is
[math]\displaystyle{ \begin{align} \qquad P_0 &= \tau \cdot \vec{u}_{o} \\ &= C_d \rho_{a} |\vec{u}_{a}| \vec{u}_{a} \cdot \vec{u}_{o} \end{align} }[/math].
Furthermore, if the relative wind stress parameterization is used, the work done on the ocean is given by
[math]\displaystyle{ \begin{align} \qquad P_1 &= \tau_{rel} \cdot \vec{u}_{o} \\ &= C_d \rho_{a} |\vec{u}_{a}-\vec{u}_{o}| (\vec{u}_{a}-\vec{u}_{o}) \cdot \vec{u}_{o} \\ &= C_d \rho_{a} |\vec{u}_{a}-\vec{u}_{o}| \vec{u}_{a} \cdot \vec{u}_{o} - C_d \rho_{a} |\vec{u}_{a}-\vec{u}_{o}| \vec{u}_{o} \cdot \vec{u}_{o} \end{align} }[/math]
Then, assuming [math]\displaystyle{ \vec{u}_o }[/math] is the same in both situations, the difference between work done by resting ocean wind stress and relative wind stress is given by
[math]\displaystyle{ \qquad P_0 - P_1 = C_d \rho_{a} |\vec{u}_{a}-\vec{u}_{o}| \vec{u}_{o} \cdot \vec{u}_{o} - C_d \rho_{a} (|\vec{u}_{a}-\vec{u}_{o}| - |\vec{u}_a|) \vec{u}_{a} \cdot \vec{u}_{o} }[/math].
Analysing this expression, we first see that the term [math]\displaystyle{ C_d \rho_{a} |\vec{u}_{a}-\vec{u}_{o}| \vec{u}_{o} \cdot \vec{u}_{o} }[/math] is always positive (since [math]\displaystyle{ \vec{u}_o \cdot \vec{u}_o = |\vec{u}_o|^2 \gt 0 }[/math] and all the other terms are positive). Next, for the term [math]\displaystyle{ - C_d \rho_{a} (|\vec{u}_{a}-\vec{u}_{o}| - |\vec{u}_a|) \vec{u}_{a} \cdot \vec{u}_{o} }[/math], we have:
- if [math]\displaystyle{ \vec{u}_{a} \cdot \vec{u}_{o} \lt 0 }[/math] then [math]\displaystyle{ |\vec{u}_{a}-\vec{u}_{o}| - |\vec{u}_a| \gt 0 }[/math] and so the overall sign is positive.
- if [math]\displaystyle{ \vec{u}_{a} \cdot \vec{u}_o \gt 0 }[/math] then [math]\displaystyle{ |\vec{u}_{a}-\vec{u}_{o}| - |\vec{u}_a| \lt 0 }[/math] and again, the overall sign is positive.
Therefore, it is always the case that [math]\displaystyle{ P_0 - P_1 \gt 0 }[/math], meaning the calculation of the work done is always larger when using the resting ocean wind stress.[6] This overestimate is referred to in the literature as a "positive bias".[1][3] Note that this may not be the case if the [math]\displaystyle{ \vec{u}_o }[/math] used in the calculation of [math]\displaystyle{ P_0 }[/math] is different from the [math]\displaystyle{ \vec{u}_o }[/math] used in the calculations of [math]\displaystyle{ P_1 }[/math] (See section: Ocean currents as output of ocean models).[6]
Wind mechanical damping effect
The mathematical explanation for the positive bias in the calculation of work using the resting ocean wind stress can also be interpreted physically through the mechanical damping effect.[3]
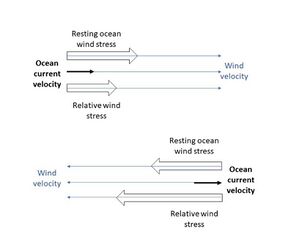
As seen in Figure 2, when the wind velocity and ocean current velocity are in the same direction, the relative wind stress is smaller than the resting ocean wind stress. In other words, less positive work is using relative wind stress. When the wind and the ocean velocities are in opposite directions, then the relative wind stress does more negative work than the resting ocean wind stress. Consequently, in both scenarios less work is being done on the ocean when the relative wind stress is used for the calculation.
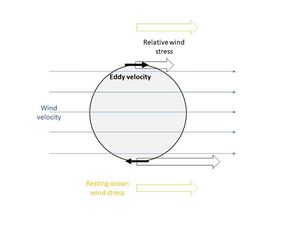
This physical interpretation can also be adapted to a scenario where there is an ocean eddy. As illustrated on the top part of Figure 3, in the eddy situation, the relative wind stress is smaller when the wind and ocean velocities are aligned, a similar situation to the top part of Figure 2. At the bottom part of Figure 3 we have a situation analogous to the bottom part of Figure 2, where more negative work is being performed on the system than in the resting ocean case. Therefore, at the top of the eddy less energy is being put in and at the bottom more energy is being taken out, which means the eddy is being dampened more in the relative wind case.
The two situations depicted in Figures 2 and 3 are the physical reason why there is a positive bias when estimating the power (work per unit time) input to the ocean when using the resting ocean stress rather than the relative wind stress [3].[7]
Impact on models for large-scale ocean circulation
For the computation of surface currents, a general circulation model is forced with surface winds. A study by Pacanowski (1987)[8] shows that including ocean current velocity through relative wind stress in an Atlantic circulation model reduces the surface currents by 30%.[9] This decrease in surface current can impact sea surface temperature and upwelling along the equator. However, the greatest impact of including ocean currents in the air-sea stress is in the calculation of Power input to the general circulation, with the mechanism as described above. An additional effect of the computation with relative wind stress instead of resting ocean wind stress leads to a lower Residual Meridional Overturning Circulation in models.
Power Input
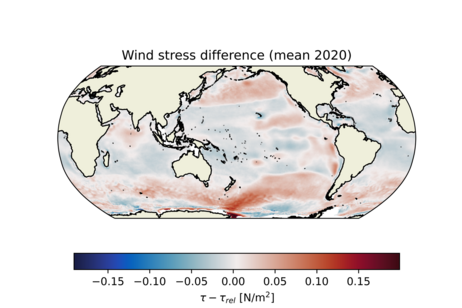
Figure 4 shows the difference between relative wind stress and resting ocean wind stress. Data for relative wind stress is obtained from scatterometers. These accurately represent the relative wind stress as they measure backscatter from small-scale structures on the ocean surface, which respond to the sea surface-air interface and not to wind speed.
Overestimations of power input into the ocean in models have been identified when using wind stress calculated from zonal mean wind instead of relative wind stress, ranging between 20-35%.[11][12][6] In regions where wind speeds are relatively low and current speeds relatively high this effect is the greatest. An example is the tropical Pacific ocean where trade winds blow with 5-9m/s and the ocean current velocities can exceed 1m/s.[13] In this region, depending on if it is an El Niño or La Niña state, the wind stress difference (resting ocean wind stress minus relative wind stress) can vary between negative and positive, respectively.
Residual Meridional Overturning Circulation
In the Southern Ocean, the use of relative wind stress is important because eddies are crucial in the Antarctic Circumpolar Circulation, and the damping of these eddies with relative wind stress will affect the overturning circulation. The Residual Meridional Overturning Circulation (RMOC), is a streamfunction that quantifies the transport of tracers across isopycnals.[14] Wind stress is taken into account through the formulation of the RMOC, which is the sum of the Eulerian mean MOC [math]\displaystyle{ \bar{\Psi} }[/math] and eddy-induced bolus overturning [math]\displaystyle{ \Psi^* }[/math]. The Eulerian mean MOC is dependent on the meridional winds that drive Ekman transport in zonal direction. The eddy-induced bolus overturning acts to restore sloping isopycnals to the horizontal, which are induced by eddies. The formulation of the RMOC is given by:
[math]\displaystyle{ \begin{align} \Psi_{res}= \bar{\Psi} + \Psi^* = \frac{-\bar{\tau}_x }{\rho_0 f} + Ks \end{align} }[/math]
with [math]\displaystyle{ \bar{\tau}_x }[/math] being the zonal mean wind stress, [math]\displaystyle{ \rho_0 }[/math] the reference density, [math]\displaystyle{ f }[/math] the Coriolis parameter (negative in Southern Hemisphere), [math]\displaystyle{ K }[/math] the quasi-Stokes eddy diffusivity field, equal to [math]\displaystyle{ L_{eddy} \cdot U_{eddy} }[/math] being the length and the velocity of the eddy, respectively, and [math]\displaystyle{ s }[/math] the slope of the isopycnals.
Inserting a lower wind stress, by using relative wind stress instead of resting ocean wind stress, directly leads to lower residual overturning, by reducing the Eulerian mean MOC ([math]\displaystyle{ \bar{\Psi} }[/math]). Furthermore, it affects the eddy-induced bolus overturning ([math]\displaystyle{ \Psi^* }[/math]) by damping eddies which results in reduced length and velocity scale ([math]\displaystyle{ L_{eddy} }[/math] & [math]\displaystyle{ U_{eddy} }[/math]) of eddies. The sum of this thus leads to a lower [math]\displaystyle{ \Psi_{res} }[/math].
Ocean currents as output of ocean models
As briefly mentioned in Section: Impact on Models for large-scale Ocean Circulation, the surface currents can be calculated by forcing surface winds into a general circulation model. The case of a model which is also forced by relative wind stress can be visualized in Figure 5. Firstly, the satellite data is used to input the 10m wind velocity into the calculation of the relative wind stress. However, if the parameterization for relative wind stress is used, this will result in a coupled problem. The ocean model requires the relative wind stress [math]\displaystyle{ \tau_{rel} }[/math] to output the ocean current velocity, which in turn the calculation of [math]\displaystyle{ \tau_{rel} }[/math] relies on.[15] This coupled system needs to be formulated as an inverse problem.
Another consequence is that, depending on the parameterization used for the wind stress, a different vector field will be inputted into the ocean model and, consequently, a different value of [math]\displaystyle{ \vec{u}_o }[/math] will be outputted by the ocean model. Therefore, if a different wind field [math]\displaystyle{ \vec{u}_o }[/math] is used for the calculations of [math]\displaystyle{ P_0 }[/math] and [math]\displaystyle{ P_1 }[/math] then it could be that [math]\displaystyle{ P_0 - P_1 \lt 0 }[/math]. In other words, there may be a negative bias when calculating the work done on the ocean using the resting ocean approximation.[7] On the global scale, however, the literature has found an over rather than underestimation, as previously mentioned.[3]
References
- ↑ 1.0 1.1 Ferrari, Raffaele; Wunsch, Carl (1 January 2009). "Ocean Circulation Kinetic Energy: Reservoirs, Sources, and Sinks". Annual Review of Fluid Mechanics 41 (1): 253–282. doi:10.1146/annurev.fluid.40.111406.102139. Bibcode: 2009AnRFM..41..253F.
- ↑ 2.0 2.1 2.2 "Data | Copernicus Marine". https://resources.marine.copernicus.eu/product-detail/WIND_GLO_WIND_L3_REP_OBSERVATIONS_012_005/DATA-ACCESS.
- ↑ 3.0 3.1 3.2 3.3 3.4 Zhai, Xiaoming; Johnson, Helen L.; Marshall, David P.; Wunsch, Carl (1 August 2012). "On the Wind Power Input to the Ocean General Circulation". Journal of Physical Oceanography 42 (8): 1357–1365. doi:10.1175/JPO-D-12-09.1. Bibcode: 2012JPO....42.1357Z.
- ↑ Dawe, Jordan T.; Thompson, LuAnne (2006). "Effect of ocean surface currents on wind stress, heat flux, and wind power input to the ocean" (in en). Geophysical Research Letters 33 (9): L09604. doi:10.1029/2006GL025784. ISSN 0094-8276. Bibcode: 2006GeoRL..33.9604D.
- ↑ Duhaut, Thomas H. A.; Straub, David N. (2006-02-01). "Wind Stress Dependence on Ocean Surface Velocity: Implications for Mechanical Energy Input to Ocean Circulation" (in en). Journal of Physical Oceanography 36 (2): 202–211. doi:10.1175/JPO2842.1. ISSN 1520-0485. Bibcode: 2006JPO....36..202D.
- ↑ 6.0 6.1 6.2 Zhai, Xiaoming; Greatbatch, Richard J. (2007-02-22). "Wind work in a model of the northwest Atlantic Ocean". Geophysical Research Letters 34 (4). doi:10.1029/2006gl028907. ISSN 0094-8276. Bibcode: 2007GeoRL..34.4606Z. https://agupubs.onlinelibrary.wiley.com/doi/full/10.1029/2006GL028907.
- ↑ 7.0 7.1 Hughes, Chris W.; Wilson, Chris (2008-02-20). "Wind work on the geostrophic ocean circulation: An observational study of the effect of small scales in the wind stress" (in en). Journal of Geophysical Research 113 (C2): C02016. doi:10.1029/2007JC004371. ISSN 0148-0227. Bibcode: 2008JGRC..113.2016H. http://doi.wiley.com/10.1029/2007JC004371.
- ↑ Pacanowski, R. C. (1987-06-01). "Effect of Equatorial Currents on Surface Stress" (in EN). Journal of Physical Oceanography 17 (6): 833–838. doi:10.1175/1520-0485(1987)017<0833:EOECOS>2.0.CO;2. ISSN 0022-3670. Bibcode: 1987JPO....17..833P.
- ↑ Dawe, Jordan T.; Thompson, LuAnne (2006). "Effect of ocean surface currents on wind stress, heat flux, and wind power input to the ocean". Geophysical Research Letters 33 (9). doi:10.1029/2006gl025784. ISSN 0094-8276. Bibcode: 2006GeoRL..33.9604D.
- ↑ "NCEP Global Ocean Data Assimilation System (GODAS) at NOAA ESRL/PSL: NOAA Physical Sciences Laboratory". https://psl.noaa.gov/data/gridded/data.godas.html.
- ↑ Duhaut, Thomas H. A.; Straub, David N. (2006-02-01). "Wind Stress Dependence on Ocean Surface Velocity: Implications for Mechanical Energy Input to Ocean Circulation" (in EN). Journal of Physical Oceanography 36 (2): 202–211. doi:10.1175/JPO2842.1. ISSN 0022-3670. Bibcode: 2006JPO....36..202D.
- ↑ Zhai, Xiaoming; Johnson, Helen L.; Marshall, David P.; Wunsch, Carl (2012-08-01). "On the Wind Power Input to the Ocean General Circulation" (in EN). Journal of Physical Oceanography 42 (8): 1357–1365. doi:10.1175/JPO-D-12-09.1. ISSN 0022-3670. Bibcode: 2012JPO....42.1357Z. https://journals.ametsoc.org/view/journals/phoc/42/8/jpo-d-12-09.1.xml.
- ↑ Kelly, Kathryn A.; Dickinson, Suzanne; McPhaden, Michael J.; Johnson, Gregory C. (2001-06-15). "Ocean currents evident in satellite wind data". Geophysical Research Letters 28 (12): 2469–2472. doi:10.1029/2000gl012610. ISSN 0094-8276. Bibcode: 2001GeoRL..28.2469K. https://agupubs.onlinelibrary.wiley.com/doi/epdf/10.1029/2000GL012610.
- ↑ Young, William R. (2012-05-01). "An Exact Thickness-Weighted Average Formulation of the Boussinesq Equations" (in en). Journal of Physical Oceanography 42 (5): 692–707. doi:10.1175/JPO-D-11-0102.1. ISSN 0022-3670. Bibcode: 2012JPO....42..692Y. http://journals.ametsoc.org/doi/10.1175/JPO-D-11-0102.1.
- ↑ Sun, Zhikuo; Small, Justin; Bryan, Frank; Tseng, Yu-heng; Liu, Hailong; Lin, Pengfei (October 2021). "The impact of wind corrections and ocean-current influence on wind stress forcing on the modeling of Pacific North Equatorial Countercurrent" (in en). Ocean Modelling 166: 101876. doi:10.1016/j.ocemod.2021.101876. Bibcode: 2021OcMod.16601876S.
 |