Physics:Flow conditioning
Flow conditioning ensures that the "real world" environment closely resembles the "laboratory" environment for proper performance of inferential flowmeters like orifice, turbine, coriolis, ultrasonic etc.
Types of flow
Basically, Flow in pipes can be classified as follows –
- Fully developed flow[clarification needed] (found in world-class flow laboratories)
- Pseudo-fully developed flow[clarification needed]
- Non-swirling, non-symmetrical flow
- Moderate swirling, non-symmetrical flow
- High swirling, symmetrical flow
Types of flow conditioners
Flow conditioners shown in fig.(a) can be grouped into following three types –
- Those that eliminate swirl only (tube bundles)
- Those that eliminate swirl and non-symmetry, but do not produce pseudo fully developed flow
- Those that eliminate swirl and non-symmetry and produce pseudo fully developed flow (high-performance flow conditioners)
Straightening devices such as honeycombs and vanes inserted upstream of the flow meter can reduce the length of straight pipe required. However, they produce only marginal improvements in measurement accuracy and may still require significant length of straight pipe, which a cramped installation site may not permit.
A flow straightener, sometimes called a honeycomb, is a device used to straighten the air flow in a wind tunnel. It is a passage of ducts, laid along the axis of main air stream to minimize the lateral velocity components caused by swirling motion in the air flow during entry. The cross-section shapes of these "honeycombs" may be of square, circular and regular hexagonal cells.
A low-cost handmade flow straightener
A low-cost flow straightener can be constructed using drinking straws, as they have low cost and good efficiency. The MythBusters television show used such a construction for their wind tunnel, as did an experimental wind tunnel at MIT (Maniet). The straws should be cut to equal size and placed in a frame.
Effectiveness of honeycomb
The effectiveness of honeycomb, in reducing the swirl and turbulence level, is studied by simulating the flow field using standard k-ε turbulence model in commercial computational fluid dynamics (CFD). CFD is the most precise and economical approach to estimate the effectiveness of a honeycomb.
Computational model
A computational domain of honeycomb is created as shown in Fig. 1
We know computationally, it is very difficult to provide the realistic non-uniform flow at the entry of honeycomb as experienced in the experiments. Such random inlet conditions would essentially simulate the realistic case in which air can enter the honeycomb from any direction and at any level of turbulence. Therefore, special domain is designed for introducing practical inlet condition
Meshing of Computational Models
The solid model of honeycomb is meshed in GAMBIT 2.3.16. As shown in Fig. 2. A structured rectangular mesh is used for the simulation with square honeycomb configuration. Governing equations for mass and momentum conservations for subsonic flow along with the equations for turbulence and porous flow are solved for the honeycomb using commercial CFD. RANS type RNG k-ε model is used for the turbulence modeling.
Boundary Conditions
The separate domain created upstream of the honeycomb is provided with various inlet conditions to arrive at the disorderly motion at the exit, which should be given as an inlet to the honeycomb cells. This essentially simulates the more realistic case that the flow can enter into the honeycomb from any direction. Specifications of this inlet along with other necessary boundary conditions are mentioned here. Flow at the inlet of the honeycomb shall necessarily have turbulent and swirling motions. Therefore, in order to incorporate these requirements, a separate fluid domain is constructed.
Top and bottom circular faces are considered as inlet to this domain to get a flow field with higher magnitude of lateral velocity. This domain is provided with vertical and horizontal cylinders as an obstruction to the inlet to produce sufficient swirling at the exit of this section. A tetrahedral mesh as shown in Fig. 3 with tetrahedral elements is generated for this geometry. The number of nodes are 1,47,666. Three faces of this configuration are specified as inlets with velocity boundary conditions. Fluid velocity at these inlet faces has been so taken that averaged mean velocity at the outlet is 1 m/s, which is in the operational wind tunnel.
A pressure outlet boundary condition is used at exit of the settling chamber where pressure at outlet is set to zero for gauge pressure. It is always possible to predict the entire flow field by meshing whole fluid domain; however simulation for the prediction of entire flow field using symmetry boundary condition. This approach reduces the mesh requirement and computational efforts. Therefore, symmetry boundary is used at the periphery of the computational domain.
All the solid boundaries in the computational domain are specified as viscous walls with no-slip wall boundary condition. Turbulence intensity profile at the exit of turbulence model is shown in Fig. 4. This figure shows the turbulence intensity and which is maximum at the center (30%) and at the walls is around 16-18%, now this profile is incorporated inside the honeycomb as shown in Fig. 2, the profile of turbulence intensity comes out from the honeycomb is shown in Fig. 5. In this profile we can see that the turbulence intensity is reduced from 30% to 1.2% at the center and 16% to 3.5%, it means the honeycomb effectiveness is very high which is around 96%.
Natural gas measurement
Natural gas that carries a lot of liquids with it is known as wet gas whereas natural gas that is produced without liquid is known dry gas. Dry gas is also treated as to remove all liquids. The effect of flow conditioning for various popular meters which is used in gas measurement is explained below.
Pipe flow conditions
The most important as well as most difficult to measure aspects of flow measurement are flow conditions within a pipe upstream of a meter. Flow conditions mainly refer to the flow velocity profile, irregularities in the profile, varying turbulence levels within the flow velocity or turbulence intensity profile, swirl and any other fluid flow characteristics which will cause the meter to register flow different than that expected. It will change the value from the original calibration state referred to as reference conditions that are free of installation effects.[1]
Installation effects
Installation effects such as insufficient straight pipe, exceptional pipe roughness or smoothness, elbows, valves, tees and reducers causes the flow conditions within the pipe to vary from the reference conditions. How these installation effects impact the meter is very important since devices which create upstream installation effects are common components of any standard metering design. Flow Conditioning refers to the process of artificially generating a reference, fully developed flow profile and is essential to enable accurate measurement while maintaining a cost-competitive meter standard design. The meter calibration factors are valid only of geometric and dynamic similarity exists between the metering and calibration conditions. In fluid mechanics, this is commonly referred to as the Law of Similarity.[2]
Law of similarity
The principle of Law of Similarity is used extensively for theoretical and experimental fluid machines. With respect to calibration of flowmeters, the Law of Similarity is the foundation for flow measurement standards. To satisfy the Law of Similarity, the central facility concept requires geometric and dynamic similarity between the laboratory meter and the installed conditions of this same meter over the entire custody transfer period. This approach assumes that the selected technology does not exhibit any significant sensitivity to operating or mechanical variations between calibrations. The meter factor determined at the time of calibration is valid if both dynamic and geometric similarity exists between the field installation and the laboratory installation of the artifact. A proper manufacturer's experimental pattern locates sensitive regions to explore, measure and empirically adjust. The manufacturer's recommended correlation method is a rational basis for performance prediction provided the physics do not change. For instance, the physics are different between subsonic and sonic flow. To satisfy the Law of Similarity the in situ calibration concept requires geometric and dynamic similarity between the calibrated meter and the installed conditions of this same meter over the entire custody transfer period. This approach assumes that the selected technology does not exhibit any significant sensitivity to operating or mechanical variations between calibrations. The meter factor determined at the time of calibration is valid if both dynamic and geometric similarity exists in the "field meter installation" over the entire custody transfer period.[3]
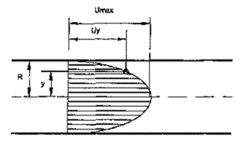
Velocity flow profile
The most commonly used description of flow conditions within the pipe is the flow velocity profile. Fig.(1) shows the typical flow velocity profile for natural gas measurement.[4] The shape of the flow velocity profile is given by the following equation,
[math]\displaystyle{ {\frac{U_y}{U_{max}}} = \left [ 1 - \frac{Y}{R} \right ]^{1/n} }[/math] ---- (1)
The value of n determines the shape of the flow velocity profile. The eq.(1) can be used to determine the flow profile's shape within the pipe by fitting a curve to experimentally measured velocity data. In 1993, the transverse flow velocities were being measured within the high pressure natural gas environment using hot wire technology to accomplish the data fit. A fully developed flow profile was used as the reference state for meter calibration and determination of Coefficient of Discharge (Cd). For Reynolds Number [math]\displaystyle{ 10^5 }[/math] to [math]\displaystyle{ 10^6 }[/math] n is approximately 7.5; for Re of [math]\displaystyle{ 10^6 }[/math], n is approximately 10.0 where a fully developed profile in a smooth pipe was assumed. Since n is a function of Reynolds Number and friction factor, more accurate values of n can be estimated by using the eq.(2),
[math]\displaystyle{ n = \frac {1}{\sqrt{f}}. }[/math] ---- (2)
Where, f is friction factor.[5] A good estimate of a fully developed velocity profile can be used for those without adequate equipment to actually measure the flow velocities within the pipe. The following straight pipe equivalent length in eq.(3) was utilized to ensure a fully developed flow profile exists.[6]
[math]\displaystyle{ Pipe Diameters = 4.4D \left [R_e \right ]^{1/6} }[/math] ---- (3)
In eq.(3) the pipe lengths required is significant, hence we need some devices that can able to condition the flow over a shorter pipe length allowing metering packages to be cost competitive and accurate. Here the velocity flow profile is generally three-dimensional. Normally the description requires no axial orientation indication if the profile is asymmetric and if it does exists, then axial orientation with respect to some suitable plane of reference is required. Asymmetry exists downstream of installation effects such as elbows or tees. Usually, the velocity flow profile is described on two planes 90° apart. Using the latest software technology a full pipe cross sectional description of the velocity profile is possible provided sufficient data points are given.
Turbulence intensity
The second description of the flow field state within the pipe is the turbulence intensity. According to an experiment in 1994, the metering errors may exist even when the velocity flow profile is fully developed with perfect pipe flow conditions. Conversely, it was found zero metering error at times when the velocity profile was not fully developed. Hence this behavior was referred to the turbulence intensity of the gas flow that can cause metering bias error. This behavior accounts in part for the less than adequate performance of the conventional tube bundle.[7]
Swirl
The third description of the flow field's state is swirl. Swirl is the tangential flow component of the velocity vector. The velocity profile should be referred to as the axial velocity profile. As the velocity vector can be resolved into three mutually orthogonal components, the velocity profile only represents the axial component of velocity. fig.(2) showing the Swirl Angle which explains the definition of flow swirl and swirl angle. Note that swirl is usually referenced to full body rotation (that which the full pipeline flow follows one axis of swirl). In real pipeline conditions, such as downstream of elbows two or more mechanisms of swirl may be present.
Effects on flow measurement devices
The condition of a flow can affect the performance and accuracy of devices that measure the flow.
Effects of flow conditioning on Orifice meter
The basic orifice mass flow equation provided by API 14.3 and ISO 5167 is given as,
[math]\displaystyle{ q_m = (C_d)(E_v)(Y)\left [ \frac{\pi}{4} \right ](d)^2 \sqrt {2 \rho \Delta P} }[/math] ----(4)
Where,
[math]\displaystyle{ q_m }[/math] = Mass flow
[math]\displaystyle{ C_d }[/math] = Coefficient of discharge
[math]\displaystyle{ E_v }[/math] = Velocity of approach factor
Y = Expansion factor
d = orifice diameter
[math]\displaystyle{ \rho }[/math] = density of the fluid
[math]\displaystyle{ \Delta P }[/math] = differential pressure
Now to use the eq.(4), the flow field entering the orifice plate must be free of swirl and exhibit a fully developed flow profile. API 14.3 (1990) and ISO standards determined the Coefficient of Discharge by completing numerous calibration tests where the indicated mass flow was compared to the actual mass flow to determine coefficient of discharge. In all testing the common requirement was a fully developed flow profile entering the orifice plate.[8] Accurate standard compliant meter designs must therefore ensure that a swirl free, fully developed flow profile is impinging on the orifice plate. There are numerous methods available to accomplish this. These methods are commonly known as "flow conditioning".
The first installation option is to revert to no flow conditioning, but adequate pipe lengths must be provided by the eq.(2) mentioned above. This generally makes the manufacturing costs for a flow measurement facility unrealistic due to excessively long meter tubes; Imagine meter tubes 75 diameters long.
The second and most well known option is the 19-tube tube-bundle flow conditioner. The majority of flow installations in North America contain the tube bundle. With the help of hot wire, pitot tube and laser-based computerized measurement systems which allow detailed measurement of velocity profile and turbulence intensity; we know that the tube bundle does not provide fully developed flow.[9] Therefore, this device is causing biased orifice flow measurement. As a result of these recent findings, few tube bundles are specified for flow measurement and reduce the use of such device. Numerous references are available providing performance results indicating less than acceptable meter performance when using the conventional 19-tube test bundle.[10] The individual results should be reviewed to ascertain details such as beta ratio, meter tube lengths, Re and test conditions.
The general indications are that the conventional tube bundle will cause the orifice installation to over register flow values up to 1.5% when the tube bundle is 1 pipe diameter to approximately 11 pipe diameters from the orifice plate. This is caused by a flat velocity profile that creates higher differential pressures than with a fully developed profile. There is a crossover region from approximately 10 to 15 pipe diameters where the error band is approximately zero. Then a slight under-registration of flows occurs for distances between approximately 15 to 25 pipe diameters. This is due to a peaked velocity profile that creates lower differential pressures than a fully developed profile. At distances greater than 25 pipe diameters the error asymptotes to zero. Fig.(3) showing the Conventional Tube Bundle Performance explaining typical characteristic behavior of the popular 19 tube, tube-bundle. An additional drawback of the conventional 19 tube, tube bundle is variation in sizing. The conventional tube bundle provides errors very much dependent on installation details, that is, the elbows on and out of plane, tees, valves and distances from the last pipe installation to the conditioner and conditioner to the orifice plate. These errors have a great significance. Therefore, the latest findings regarding conventional tube bundle performance should be reviewed prior to meter station design and installation. The final installation option for orifice metering is perforated plate flow conditioners. There is a variety of perforated plates have entered the market. These devices generally are designed to rectify the drawbacks of the conventional tube bundle (accuracy and repeatability insufficiency). The reader is cautioned to review the performance of the chosen perforated plate carefully prior to installation. A flow conditioner performance test guideline should be utilized to determine performance.[11] The key elements of a flow conditioner test are -
- Perform a baseline calibration test with an upstream length of 70 to 100 pipe diameters of straight meter tube. The baseline Coefficient of Discharge values should be within the 95% confidence interval for the RG orifice equation (i.e. the coefficient of discharge equation as provided by AGA-3).
- Select values of upstream meter tube length, and flow conditioner location, to be used for the performance evaluation. Install the flow conditioner at the desired location. First, perform a test for either the two 90° elbows out-of-plane installation, or the high swirl installation for [math]\displaystyle{ \beta }[/math] = 0.40 and for [math]\displaystyle{ \beta }[/math] = 0.67. This test will show whether the flow conditioner removes swirl from the disturbed flow. If the [math]\displaystyle{ \Delta Cd }[/math] is within the acceptable region for both values of [math]\displaystyle{ \beta }[/math] i.e. 0.40 and 0.67, and if the Cd results vary as [math]\displaystyle{ (\beta)^{3.5} }[/math], then the conditioner is successful in removing swirl. The tests for the other three installations namely, good flow conditions, partly closed valve and highly disturbed flow) may be performed for [math]\displaystyle{ \beta }[/math] = 0.67, and the results for other (i ratios predicted from the [math]\displaystyle{ \Delta Cd - (\beta)^{3.5} }[/math] correlation. Otherwise, the tests should be performed for a range of p ratios between 0.20 and 0.75.
- Perform test and determine the flow conditioner performance for the flow conditioner installed in good flow conditions, downstream of a half closed valve, and for either the double 90° elbow out-of-plane or the high swirl installation.
Effects of flow conditioning on turbine meter
The turbine meter is available in various manufacturer's configurations of a common theme; turbine blades and rotor configured devices. These devices are designed such that when a gas stream passes through them they will spin proportionally to the amount of gas passing over the blades in a repeatable fashion. Accuracy is then ensured by completion of a calibration, indicating the relationship between rotational speed and volume, at various Reynolds Numbers. The fundamental difference between the orifice meter and the turbine meter is the flow equation derivation. The orifice meter flow calculation is based on fluid flow fundamentals (a 1st Law of Thermodynamics derivation utilizing the pipe diameter and vena contracta diameters for the continuity equation). Deviations from theoretical expectation can be assumed under the Coefficient of Discharge. Thus, one can manufacture an orifice meter of known uncertainty with only the measurement standard in hand and access to a machine shop. The need for flow conditioning, and hence, a fully developed velocity flow profile is driven from the original determination of Cd which utilized fully developed or 'reference profiles' as explained above.
Conversely, the turbine meter operation is not rooted deeply in fundamentals of thermodynamics. This is not to say that the turbine meter is in any way an inferior device. There are sound engineering principles providing theoretical background. It is essentially an extremely repeatable device that is then assured accuracy via calibration. The calibration provides the accuracy. It is carried out in good flow conditions (flow conditions free of swirl and a uniform velocity flow profile) this is carried out for every meter manufactured. Deviations from the as-calibrated conditions would be considered installation effects, and the sensitivity of the turbine meter to these installation effects is of interest. The need for flow conditioning is driven from the sensitivity of the meter to deviations from as calibrated conditions of swirl and velocity profile. Generally, recent research indicates that turbine meters are sensitive to swirl but not to the shape of the velocity profile. A uniform velocity profile is recommended, but no strict requirements for fully developed flow profiles are indicated. Also, no significant errors are evident when installing single or dual rotor turbine meters downstream of two elbows out-of-plane without flow conditioning devices.[12][13]
Effects of flow conditioning on ultrasonic meter
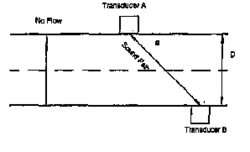
Due to the relative age of the technology, it may be beneficial to discuss the operation of the multipath ultrasonic meter to illustrate the effects of flow profile distortion and swirl. There are various types of flow measurements utilizing high frequency sound. The custody transfer measurement devices available today utilize the time of travel concept. The difference in time of flight with the flow is compared to the time of flight against the flow. This difference is used to infer average flow velocity on the sound path.[14] Fig.(5) showing the Ultrasonic Meter sound path no flow which illustrates this concept.
The resulting flow equation for the mean velocity experienced by the sound path is given by,
[math]\displaystyle{ \bar {V}_{flow} = \left [ \frac{1}{T_{ab}} - \frac{1}{T_{ba}} \right ]\left [ \frac{Dist_{Sound path}}{2\cos \phi} \right ] }[/math] ----(5)
The case of no flow gives the actual path of the sound when there is zero flow (by equating eq.(5) to zero). In case of theoretical flow profile, say a uniform velocity flow profile where the no-slip condition on the pipe walls is not applied, Fig.(6) shows Ultrasonic Meter sound path - uniform velocity profile which illustrates the resultant sound path.
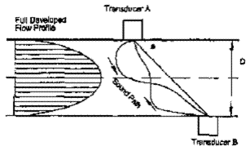
A theoretical derivation of the Mean velocity equation for this sound path becomes much more complicated. In case of a perfect fully developed real velocity profile of Ultrasonic meter which is shown in Fig.(7) indicating a possible sound path as a result of an installation in a real flow.
Here a mathematical derivation for this Ultrasonic meter is also becomes very complicated. Developing a robust flow algorithm to calculate the mean flow velocity for the sound path can be quite complicated. Now add to this; sound path reflection from the pipe wall, multipaths to add degrees of freedom, swirl and departure from axisymmetric fully developed flow profile and the problem of integrating the actual velocity flow profile to yield volume flow rate can be an accomplishment. Hence the real performance of ultrasonic meters downstream of perturbations, and the need for calibrations is required.[15]
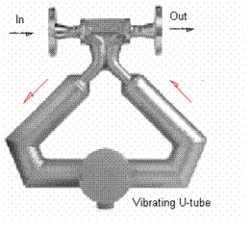
Effects of flow conditioning on Coriolis meter
Coriolis meter shown in fig.(8) is very accurate in single-phase conditions but inaccurate to measure two-phase flows. It poses a complex fluid structure interaction problem in case of two-phase operation. There is a scarcity of theoretical models available to predict the errors reported by Coriolis meter in aforementioned conditions.
Flow conditioners make no effect on meter accuracy while using wet gas due to the annular flow regime, which is not highly affected by flow conditioners. In single-phase conditions, Coriolis meter gives accurate measurement even in presence of severe flow disturbances. There is no need for flow conditioning before the meter to obtain accurate readings from it, which would be the case in other metering technologies like orifice and turbine. On the other hand, in two-phase flows, the meter consistently gives negative errors. The use of flow conditioners clearly affects the reading of the meter in aerated liquids. This phenomenon can be used to get fairly accurate estimate of flow rate in low gas volume fraction liquid flows.[16]
Liquid flow measurement
Flow conditioning makes a huge effect on the accuracy of liquid turbine meter which results in flow disturbances. These effects are mainly caused by debris on strainer screens, for various upstream piping geometries and different types of flow conditioners. The effectiveness of a flow conditioner can be indicated by the following two key measurements:
- Percentage variation of an average meter factor over the defined range of flow disturbances for a given flow rate and inlet piping geometry. The lesser the value of percentage variation of an average meter factor over the range of flow disturbances, the better will be the performance of flow conditioner.
- Percentage meter factor repeatability for each flow disturbance, at a given flow rate and inlet piping geometry. The lesser the value of percentage meter factor repeatability at a given set of installation/operating conditions, the better will be the performance of flow conditioner.
See also
- Flow measurement
- Orifice meter
- Turbine meter
- Ultrasonic flow meter
- Coriolis meter
- Fluid dynamics
- Wet gas
- Dry gas
- Orifice plate
- Mass flow meter
- Mass flow rate
- Volumetric flow rate
References
- ↑ Miller, W. Richard, "Flow Measurement Engineering Handbook", McGraw-Hill, Third Edition, 1996, ISBN:0-07-042366-0
- ↑ Flow conditioning for Natural gas measurement
- ↑ The effects of flow conditioning
- ↑ Karnik, U., "Measurements of the Turbulence Structure Downstream of a Tubs Bundle at High Reynolds Numbers", ASME Fluids Engineering Meeting, Washington D.C., June 1993
- ↑ Colebrook, C.F., 'turbulent Flow in Pipes, with Particular reference to the Transition between the Smooth and Rough Pipe Laws", J. Inst Clv. Eng., vol. 11, pp. 133-136, 1938-1939
- ↑ White M. Frank, "Fluids Mechanics", Second Edition, McGraw-Hill, 1986, ISBN:0-07-069673-X
- ↑ Kamlk U., Jungowskl W.M., Botros -K., "Effect of Turbulence on Orifice Meter Performance", 11'" International Symposium and Exhibition on Offshore Mechanics and Arctic Engineering, ASME, May 1994, Vol. 116
- ↑ Scott L.J., Brennan J. A., Blakeslee, NIST, U.S. Department of Commerce, National Institute of Standards and Technology, "NIST DataBase 45 GRI/KIST Orifice Meter Discharge Ceoffcient", Version 1.0 N1ST Standard Reference Data Program, Gaithersberg, MD (1994)
- ↑ Kamlk, U., "A compact Orifice Meter/Flow Conditioner Package", 3rd international Symposium of Fluid Flow Measurement, San Antonio, Texas., March, 1995
- ↑ Morrow, T.B., 'Orifice Meter Installation effects in the GRl MRF", 3rd International Symposium of Fluid Flow Measurement, San Antonio Tx., March, 1995
- ↑ Morrow T. B., Metering Research Facility Program, " Orifice Meter Installations Effects, Development of a Flow Conditioner Performance Test', GRI-9710207. Dec. 1997.
- ↑ Park J.T., "Reynolds Number and Installation Effects on Turbine Meters", Fluid Flow Measurement 3r6 International Symposium, March 1995
- ↑ Micklos J.P., "Fundamentals of Gas Turbine Meters", American School of Gas Measurement Technology 1997 Proceedings p. 35
- ↑ Stuart J.S., "New A,G.A. Report No. 9, Measurement of Gas by Multipath Ultrasonic Gas Meters", 1997 Operating Section Proceedings, Nashville, TN., May, 1997
- ↑ Kamik U., Studzinskl W., Geerligs J., Rogi M., "Performance Evaluation of 8 Inch Mutipath Ultrasonic Meters", A.G.A. operating Section Operations Conference, May, 1997, Nashville TN.
- ↑ The effect of flow conditioning on straight tube Coriolis meter
Bibliography
- ANSYS Inc., 2007. Release 11 Documentation for ANSYS Workbench.
- Cermak, J.E., 2003. Wind-tunnel development and trends in applications to civil engineering. J. Wind Eng. Ind. Aerodyn. 91 (3), 355–370.
- Cermak, J.E., Cochran, L.S., 1992. Physical modeling of the atmospheric surface layer. J. Wind Eng. Ind. Aerodyn. 41–44, 935–946.
- Collar, A.R., 1939. The effect of a gauze on velocity distribution in a uniform duct. Aeronaut. Res. Counc. Rep. Memo No. 1867. Desai, S.S., 2003.
- Relative roles of computational fluid dynamics and wind tunnel testing in the development-of aircraft. Curr. Sci. 84 (1), 49–64.
- Derbunovich, G.I., Zemskaya, A.S., Repik, E.U., Sosedko, Y.P., 1993. Optimum Conditions of Turbulence Reduction with Screens, Mechanics of Nonuniform and Turbulent Flows. Nauka, Moscow, pp. 35.
- Dryden, H.I., Schubauer, G.B., 1947. The use of damping screens for the reduction of wind tunnel turbulence. J. Aeronautical Sci. 14, 221–228.
- Farell, C., Youssef, S., 1996. Experiments on turbulence management using screens and honeycombs. ASME J. Fluids Eng. 118, 26–32.
- Ghani, S.A.A.A., Aroussi, A., Rice, E., 2001. Simulation of road vehicle natural environment in a climatic wind tunnel. Simul. Pract. Theory 8 (6–7), 359–375.
- Gordon, R., Imbabi, M.S., 1998. CFD simulation and experimental validation of a new closed circuit wind/water tunnel design. J. Fluids Eng. Trans. ASME 120 (2), 311–318.
- Groth, J., Johansson, A., 1988. Turbulence reduction by screens. J. Fluids Mech. 197, 139–155.
- Hansen, S.O., Sorensen, E.G., 1985. A new boundary-layer wind tunnel at the Danish Maritime Institute. J. Wind Eng. Ind. Aerodyn. 18, 213–224.
 |