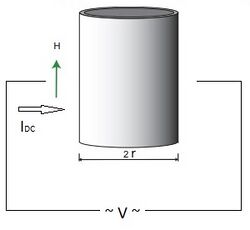
Physics:Little–Parks effect

The Little–Parks effect was discovered in 1962 by William A. Little and Ronald D. Parks in experiments with empty and thin-walled superconducting cylinders subjected to a parallel magnetic field. It was one of the first experiments to indicate the importance of Cooper-pairing principle in BCS theory. The essence of the Little–Parks (LP) effect is slight suppression of the cylinder's superconductivity by persistent current.

Explanation

The electrical resistance of such cylinders shows a periodic oscillation with the magnetic flux piercing the cylinder, the period being

h/2e ≈ 2.07×10⁻¹⁵ T⋅m²

where h is the Planck constant and e is the electron charge. The explanation provided by Little and Parks is that the resistance oscillation reflects a more fundamental phenomenon, i.e. periodic oscillation of the superconducting critical temperature T_c.

Schematic image of the Little–Parks experiment

The Little–Parks effect consists in a periodic variation of the T_c with the magnetic flux, which is the product of the magnetic field (coaxial) and the cross sectional area of the cylinder. T_c depends on the kinetic energy of the superconducting electrons. More precisely, the T_c is such temperature at which the free energies of normal and superconducting electrons are equal, for a given magnetic field. To understand the periodic oscillation of the T_c, which constitutes the Little–Parks effect, one needs to understand the periodic variation of the kinetic energy. The kinetic energy oscillates because the applied magnetic flux increases the kinetic energy while superconducting vortices, periodically entering the cylinder, compensate for the flux effect and reduce the kinetic energy. Thus, the periodic oscillation of the kinetic energy and the related periodic oscillation of the critical temperature occur together.

The Little–Parks effect is a result of collective quantum behavior of superconducting electrons. It reflects the general fact that it is the fluxoid rather than the flux which is quantized in superconductors.

The Little–Parks effect can be seen as a result of the requirement that quantum physics be invariant with respect to the gauge choice for the electromagnetic potential, of which the magnetic vector potential A forms part.

Electromagnetic theory implies that a particle with electric charge q travelling along some path P in a region with zero magnetic field B, but non-zero A (by [math]\displaystyle{ \mathbf{B} = 0 = \nabla \times \mathbf{A} }[/math]), acquires a phase shift [math]\displaystyle{ \varphi }[/math], given in SI units by

[math]\displaystyle{ \varphi = \frac{q}{\hbar} \int_P \mathbf{A} \cdot d\mathbf{x}, }[/math]

In a superconductor, the electrons form a quantum superconducting condensate, called a Bardeen–Cooper–Schrieffer (BCS) condensate. In the BCS condensate all electrons behave coherently, i.e. as one particle. Thus the phase of the collective BCS wavefunction behaves under the influence of the vector potential A in the same way as the phase of a single electron. Therefore, the BCS condensate flowing around a closed path in a multiply connected superconducting sample acquires a phase difference Δφ determined by the magnetic flux Φ_B through the area enclosed by the path (via Stokes' theorem and [math]\displaystyle{ \nabla \times \mathbf{A} = \mathbf{B} }[/math]), and given by:

[math]\displaystyle{ \Delta\varphi = \frac{q\Phi_B}{\hbar}. }[/math]

This phase effect is responsible for the quantized-flux requirement and the Little–Parks effect in superconducting loops and empty cylinders. The quantization occurs because the superconducting wave function must be single valued in a loop or an empty superconducting cylinder: its phase difference Δφ around a closed loop must be an integer multiple of 2π, with the charge q = 2e for the BCS electronic superconducting pairs.

If the period of the Little–Parks oscillations is 2π with respect to the superconducting phase variable, from the formula above it follows that the period with respect to the magnetic flux is the same as the magnetic flux quantum, namely

[math]\displaystyle{ \Delta \Phi_B = 2\pi\hbar/2e=h/2e. }[/math]

Applications

Little–Parks oscillations are a widely used proof mechanism of Cooper pairing. One of good example is the study of the Superconductor Insulator Transition.

File:R3s4 Ya35.tif

Typical Little–Parks oscillations for different temperatures

The challenge here is to separate Little–Parks oscillations from weak (anti-)localization, as in Altshuler et al. results, where authors observed the Aharonov–Bohm effect in a dirty metallic film.

History

Fritz London predicted that the fluxoid is quantized in a multiply connected superconductor. Experimentally has been shown, that the trapped magnetic flux existed only in discrete quantum units h/2e. Deaver and Fairbank were able to achieve the accuracy 20–30% because of the wall thickness of the cylinder.

Little and Parks examined a "thin-walled" (Materials: Al, In, Pb, Sn and Sn–In alloys) cylinder (diameter was about 1 micron) at T very close to the transition temperature in an applied magnetic field in the axial direction. They found magnetoresistance oscillations with the period consistent with h/2e.

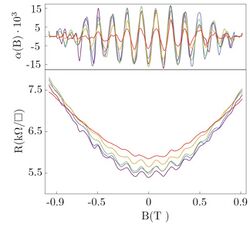
What they actually measured was an infinitely small changes of resistance versus temperature for (different) constant magnetic field, as it shown in Fig.