Chemistry:Nuclear ensemble approach

Short description: Semiclassical approach for molecular spectrum simulations.

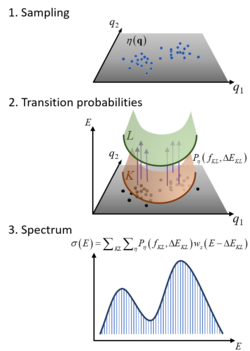
The Nuclear Ensemble Approach (NEA) is a general method for simulations of diverse types of molecular spectra. It works by sampling an ensemble of molecular conformations (nuclear geometries) in the source state, computing the transition probabilities to the target states for each of these geometries, and performing a sum over all these transitions convoluted with shape function. The result is an incoherent spectrum containing absolute band shapes through inhomogeneous broadening.

NEA simulates the spectrum in three steps: firstly an ensemble of molecular geometries is generated. 2)Secondly the transition probability between the initial and final states is computed for each geometry. Lastly a sum over all transition probabilities is done convoluted with a shape function.

Motivation

Spectrum simulation is one of the most fundamental tasks in quantum chemistry. It allows comparing the theoretical results to experimental measurements. There are many theoretical methods for simulating spectra. Some are simple approximations (like stick spectra); others are high-level, accurate approximations (like those based on Fourier-transform of wavepacket propagations). The NEA lies in between. On the one hand, it is intuitive and straightforward to apply, providing much improved results compared to the stick spectrum. On the other hand, it does not recover all spectral effects and delivers a limited spectral resolution.  

Historical

The NEA is a multidimensional extension of the reflection principle, an approach often used for estimating spectra in photodissociative systems. With popularization molecular mechanics, ensembles of geometries started to be also used to estimate the spectra through incoherent sums. Thus, different from the reflection principle, which is usually done via direct integration of analytical functions, the NEA is a numerical approach. In 2012, a formal account of NEA showed that it corresponded to an approximation to the time-dependent spectrum simulation approach, employing a Monte Carlo integration of the wavepacket overlap time evolution.

NEA for absorption spectrum

Consider an ensemble of molecules absorbing radiation in the UV/vis. Initially, all molecules are in the ground electronic state

Because of the molecular zero-point energy and temperature, the molecular geometry has a distribution around the equilibrium geometry. From a classical point of view, supposing that the photon absorption is an instantaneous process, each time a molecule is excited, it does so from a different geometry. As a consequence, the transition energy has not always the same value, but is a function of the nuclear coordinates.

The NEA captures this effect by creating an ensemble of geometries reflecting the zero-point energy, the temperature, or both.

In the NEA, the absorption spectrum (or absorption cross section) σ(E) at excitation energy E is calculated as

[math]\displaystyle{ \sigma \left( E \right)=\frac{\pi {{e}^{2}}\hbar }{2mc{{\epsilon }_{0}}E}\sum\limits_{n}^{{{N}_{fs}}}{\frac{1}{{{N}_{p}}}\sum\limits_{i}^{{{N}_{p}}}{\Delta {{E}_{0n}}\left( {{\mathbf{x}}_{i}} \right){{f}_{0n}}\left( {{\mathbf{x}}_{i}} \right)g\left( E-\Delta {{E}_{0n}}\left( {{\mathbf{x}}_{i}} \right),\delta \right)}}, }[/math]

where e and m are the electron charge and mass, c is the speed of light, ε₀ the vacuum permittivity, and ћ the reduced Planck constant. The sums run over N_fs excited states and N_p nuclear geometries x_i. For each of such geometries in the ensemble, transition energies ΔE_0n(x_i) and oscillator strengths f_0n(x_i) between the ground (0) and the excited (n) states are computed. Each transition in the ensemble is convoluted with a normalized line shape function centered at ΔE_0n(x_i) and with width δ. Each x_i is a vector collecting the cartesian components of the geometries of each atom.

The line shape function may be, for instance, a normalized Gaussian function given by

[math]\displaystyle{ g\left( E-\Delta {{E}_{0n}},\delta \right)=\frac{1}{\sqrt{2\pi {{\left( \delta /2 \right)}^{2}}}}\exp \left( -\frac{{{\left( E-\Delta {{E}_{0n}} \right)}^{2}}}{2{{\left( \delta /2 \right)}^{2}}} \right). }[/math]

Although δ is an arbitrary parameter, it must be much narrower than the band width, not to interfere in its description. As the average value of band widths is around 0.3 eV, it is a good practice to adopt δ ≤ 0.05 eV.

The geometries x_i can be generated by any method able to describe the ground state distribution. Two of the most employed are dynamics and Wigner distribution nuclear normal modes.

Molar extinction coefficient ε can be obtained from absorption cross section through

[math]\displaystyle{ \sigma = \ln(10) \frac{10^3}{N_\text{A}} \varepsilon \approx 3.823 532 16 \times 10^{-21}\,\varepsilon. }[/math]

Because of the dependence of f_0n on x_i, NEA is a post-Condon approximation, and it can predict dark vibronic bands.

NEA for emission spectrum

In the case of fluorescence, the differential emission rate is given by

[math]\displaystyle{ \Gamma(E) = \frac{ e^{2}}{2\pi \hbar mc^3 \epsilon_{0}} \frac{1}{N_{p}} \sum_{i}^{N_{p}} \Delta E_{1,0}(\mathbf{x}_{i})^2 \left | f_{1,0}(\mathbf{x}_{i})\right | g\left(E-\Delta E_{1,0}(\mathbf{x}_{i}), \delta\right) }[/math].

This expression assumes the validity of the Kasha's rule, with emission from the first excited state.

NEA for other types of spectrum

NEA can be used for many types of steady-state and time-resolved spectrum simulations. Some examples beyond absorption and emission spectra are:

• two-dimensional
• differential transmission
• photoelectron
• ultrafast Auger
• X-ray photo-scattering

Limitations of NEA

By construction, NEA does not include information about the target (final) states. For this reason, any spectral information that depends on these states cannot be described in the framework of NEA. For example, vibronically resolved peaks in the absorption spectrum will not appear in the simulations, only the band envelope around them, because these peaks depend on the wavefunction overlap between the ground and excited state. NEA can be, however, coupled to excited-state dynamics to recover these effects.

NEA may be too computationally expensive for large molecules. The spectrum simulation requires the calculation of transition probabilities for hundreds of different nuclear geometries, which may become prohibitive due to the high computational costs. Machine learning methods coupled to NEA have been proposed to reduce these costs.