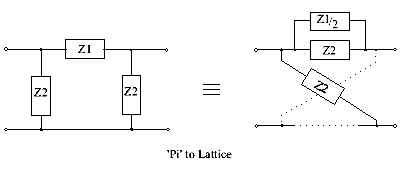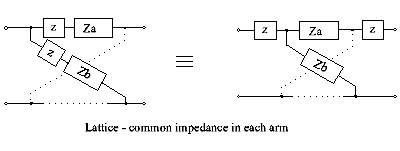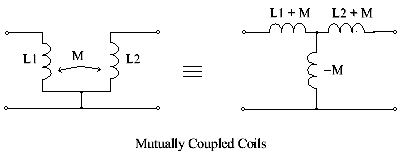Lattice network

Short description: Two-port electrical wave filter

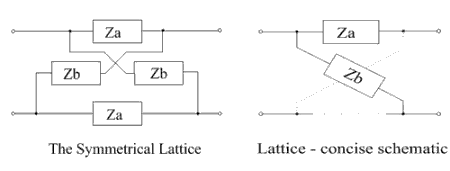
A symmetrical lattice is a two-port electrical wave filter in which diagonally-crossed shunt elements are present – a configuration which sets it apart from ladder networks. The component arrangement of the lattice is shown in the diagram below. The filter properties of this circuit were first developed using image impedance concepts, but later the more general techniques of network analysis were applied to it.

There is a duplication of components in the lattice network as the "series impedances" (instances of Z_a) and "shunt impedances" (instances of Z_b) both occur twice, an arrangement that offers increased flexibility to the circuit designer with a variety of responses achievable. It is possible for the lattice network to have the characteristics of: a delay network, an amplitude or phase correcting network, a dispersive network  or as a linear phase filter, according to the choice of components for the lattice elements.

Configuration

The basic configuration of the symmetrical lattice is shown in the left-hand diagram. A commonly used short-hand version is shown on the right, with dotted lines indicating the presence the second pair of matching impedances.

It is possible with this circuit to have the characteristic impedance specified independently of its transmission properties, a feature not available to ladder filter structures. In addition, it is possible to design the circuit to be a constant-resistance network for a range of circuit characteristics.

The lattice structure can be converted to an unbalanced form (see below), for insertion in circuits with a ground plane. Such conversions also reduce the component count and relax component tolerances.

It is possible to redraw the lattice in the Wheatstone bridge configuration (as shown in the article Zobel network). However, this is not a convenient format in which to investigate the properties of lattice filters, especially their behavior in cascade.

Basic properties

Results from image theory

Filter theory was initially developed from earlier studies of transmission lines. In this theory, a filter section is specified in terms of its propagation constant and image impedance (or characteristic impedance).

Specifically for the lattice, the propagation function, γ, and characteristic impedance, Z_o, are defined by,

[math]\displaystyle{ \gamma = \ln \left(\ \frac{\ \sqrt{ \frac{\ Z_\mathsf{a}\ }{Z_\mathsf{b}} + 1\ }\ }{\ \sqrt{\ \frac{\ Z_\mathsf{a}\ }{Z_\mathsf{b}} -1\ }\ }\ \right) = 2\ \operatorname{artanh} \sqrt{ \frac{\ Z_\mathsf{a}\ }{ Z_\mathsf{b} }\ } \qquad \; }[/math] and [math]\displaystyle{ \; \qquad Z_\mathsf{o} = \sqrt{\ Z_\mathsf{a} \cdot Z_\mathsf{b}\ } }[/math]

Once γ and Z_o have been chosen, solutions can be found for [math]\displaystyle{ \; \frac{\ Z_\mathsf{a}\ }{ Z_\mathsf{b} } \; }[/math] and [math]\displaystyle{ \; Z_\mathsf{a} \cdot Z_\mathsf{b} \; }[/math] from which the characteristics of Z_a and Z_b can each be determined. (In practice, the choices for γ and z_o are restricted to those which result in physically realisable impedances for Z_a and Z_b .) Although a filter circuit may have one or more pass-bands and possibly several stop-bands (or attenuation regions), only networks with a single pass-band are considered here.

In the pass-band of the circuit, the product Z_a × Z_b is real (i.e. Z_o is resistive) and may be equated to R_o, the terminating resistance of the filter. So

[math]\displaystyle{ Z_\mathsf{a}\ Z_\mathsf{b} = R_\mathsf{o}^2 \qquad \; }[/math] or [math]\displaystyle{ \; \qquad \frac{\ Z_\mathsf{a}\ }{ R_\mathsf{o} } = \frac{\ R_\mathsf{o}\ }{ Z_\mathsf{b} } \qquad \; }[/math] (for frequencies in the passband)

That is, the impedances behave as duals of each other within this frequency range.

In the attenuation range of the filter, the characteristic impedance of the filter is purely imaginary, and

[math]\displaystyle{ Z_\mathsf{a} = Z_\mathsf{b} \qquad \qquad \qquad \; }[/math] (for frequencies in the attenuation band)

Consequently, in order to achieve a specific characteristic, the reactances within Z_a and Z_b are chosen so that their resonant and anti-resonant frequencies are duals of each other in the passband, and match one another in the stopband. The transition region of the filter, where a change from one set of conditions to another occurs, can be made as narrow as required by increasing the complexity of Z_a and Z_b . The phase response of the filter in the pass-band is governed by the locations (spacings) of the resonant and anti-resonant frequencies of Z_a and Z_b .

For convenience, the normalised parameters  y_o  and  z_o  are defined by

[math]\displaystyle{ y_\mathsf{o} = \sqrt{\frac{\ Z_\mathsf{b}\ }{Z_\mathsf{a}}\ } = \sqrt{ \frac{\ z_\mathsf{b}\ }{z_\mathsf{a}} \ } \qquad \; }[/math] and [math]\displaystyle{ \; \qquad z_\mathsf{o} = \sqrt{\ z_\mathsf{a} \cdot z_\mathsf{b}\ } = \frac{\ Z_\mathsf{o}\ }{ R_\mathsf{o} } }[/math]

where normalised values [math]\displaystyle{ \; z_\mathsf{a} = \frac{\ Z_\mathsf{a}\ }{ R_\mathsf{o} } \; }[/math] and [math]\displaystyle{ \; z_\mathsf{b} = \frac{\ Z_\mathsf{b}\ }{ R_\mathsf{o} } \; }[/math] have been introduced. The parameter y_o is termed the index function and z_o is the normalised characteristic impedance of the network. The parameter y_o is approximately 1 in the attenuation region; z_o is approximately 1 in the transmission region.

Cascaded lattices

All high-order lattice networks can be replaced by a cascade of simpler lattices, provided their characteristic impedances are all equal to that of the original and the sum of their propagation functions equals the original. In the particular case of all-pass networks (networks which modify the phase characteristic only), any given network can always be replaced by a cascade of second-order lattices together with, possibly, one single first order lattice.

Whatever the filter requirements being considered, the reduction process results in simpler filter structures, with less stringent demands on component tolerances.

The shortcomings of image theory

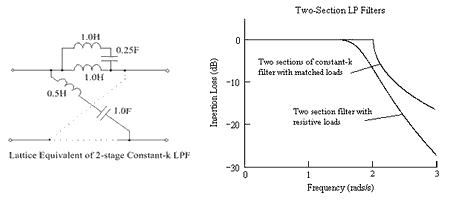
The filter characteristics predicted by image theory require a correctly terminated network. As the necessary terminations are often impossible to achieve, resistors are commonly used as the terminations, resulting in a mismatched filter. Consequently, the predicted amplitude and phase responses of the circuit will no longer be as image theory predicts. In the case of a low-pass filter, for example, where the mismatch is most severe near the cut-off frequency, the transition from pass-band to stop-band is far less sharp than expected.

The figure below illustrates the issue: A lattice filter, equivalent to two sections of constant k low-pass filter, has been derived by image methods. (The network is normalised, with [math]\displaystyle{ \; L = 1 \; }[/math] and [math]\displaystyle{ \; C = 1 \;, }[/math] so [math]\displaystyle{ \; R_\mathsf{o} = \sqrt{\ \tfrac{\ L\ }{ C }\ } = 1 \; }[/math] and [math]\displaystyle{ \; \omega_\mathsf{c} = 2\ \sqrt{\ L\ C\ } = 2 ~. }[/math] The left-hand figure gives the lattice circuit and the right-hand figure gives the insertion loss with the network terminated (1) resistively, and (2) in its correct characteristic impedances.

To minimise the mismatch problem, various forms of image filter end terminations were proposed by Zobel and others, but the inevitable compromises led to the method falling out of favour. It was replaced by the more exact methods of network analysis and network synthesis.

Results derived by network analysis

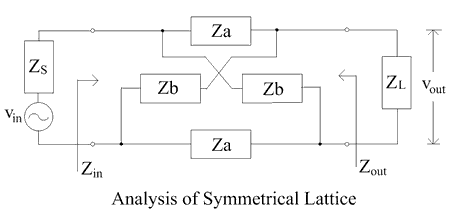
This diagram shows the general circuit for the symmetrical lattice:

Through mesh analysis or nodal analysis of the circuit, its full transfer function can be found. That is,

[math]\displaystyle{ \frac{v_\text{out}}{v_\text{in}} = \frac{Z_L(Z_b - Z_a)}{(Z_a+Z_b)(Z_S+Z_L) + 2(Z_a Z_b + Z_S Z_L)} }[/math]

The input and output impedances (Z_in and Z_out) of the network are given by

[math]\displaystyle{ \begin{align} Z_\text{in} = \frac{2 Z_a Z_b + Z_L (Z_a + Z_b)}{Z_a + Z_b + 2 Z_L} \\[1ex] Z_\text{out} = \frac{2 Z_a Z_b + Z_S (Z_a + Z_b)}{Z_a + Z_b + 2Z_S} \end{align} }[/math]

These equations are exact, for all realisable impedance values, unlike image theory where the propagation function only predicts performance accurately when Z_S and Z_L are the matching characteristic impedances of the network.

The equations can be simplified by making a number of assumptions. Firstly, networks are often sourced and terminated by resistors of the same value R₀ so that Z_S = Z_L = R₀ and the equations become

[math]\displaystyle{ \begin{align} \frac{v_\text{out}}{v_\text{in}} &= \frac{R_0(Z_b - Z_a)}{2(Z_a+R_0)(Z_b + R_0)} \\[1ex] Z_\text{in} = Z_\text{out} &= \frac{2 Z_a\, Z_b + R_0 (Z_a + Z_b)}{Z_a + Z_b + 2R_0} \end{align} }[/math]

Secondly, if the impedances Z_a and Z_b are duals of one another, so that Z_a Z_b = R₀², then further simplification is possible:

[math]\displaystyle{ \frac{v_\text{out}}{v_\text{in}} = \frac{R_0-Z_a}{2(R_0 + Z_a)} = \frac{Z_b - R_0}{2(R_0 + Z_b)} \qquad \text{and} \qquad Z_\text{in} = Z_\text{out} = R_0 }[/math]

so such networks are constant-resistance networks.

Finally, for normalised networks, with R₀ = 1,

[math]\displaystyle{ \frac{v_\text{out}}{v_\text{in}} = \frac{(1-z_a)}{2(1 + z_a)} = \frac{(z_b - 1)}{2(1+z_b)} \qquad \qquad \text{and} \qquad z_\text{in} = z_\text{out} = 1 }[/math]

If the impedances Z_a and Z_b (or the normalised impedances z_a and z_b) are pure reactances, then the networks become all-pass, constant-resistance, with a flat frequency response but a variable phase response. This makes them ideal as delay networks and phase equalisers.

When resistors are present within Z_a and Z_b then, provided the duality condition still applies, a circuit will be constant-resistance but have a variable amplitude response. One application for such circuits is as amplitude equalisers.

Conversions and equivalences

(See references)

T to lattice

Pi to lattice

Common series element

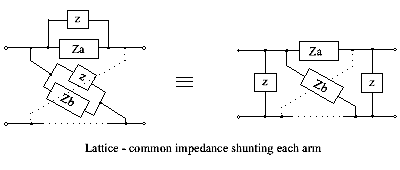
Common parallel element

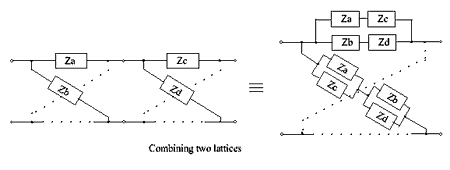
Combining two lattices into one

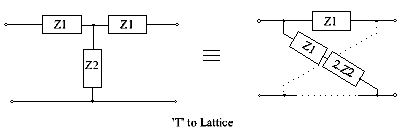
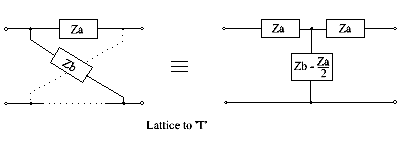
Lattice to T (see also the next section)

This lattice-to-T conversion only gives a realisable circuit when the evaluation of (Z_b − Z_a) / 2 gives positive valued components. For other situations, the bridged-T may provide a solution, as discussed in the next section.

Unbalanced equivalents

The lattice is a balanced configuration which is not suitable for some applications. In such cases it is necessary to convert the circuit to an electrically equivalent unbalanced form. This provides benefits, including reduced component count and relaxed circuit tolerances. The simple conversion procedure shown in the previous section can only be applied in a limited set of conditions – generally, some form of bridged-T circuit is necessary. Many of the conversions require the inclusion of a 1:1 ideal transformer, but there are some configurations which avoid this requirement, and one example is shown below.

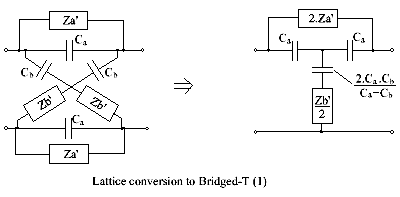
This conversion procedure starts by using the property of a lattice where a common series element in all arms can be taken outside the lattice as two series elements (as shown above). By repeatedly applying this property, components can be extracted from within the lattice structure. Finally, by means of Bartlett's bisection theorem, an unbalanced bridged-T circuit is achieved.

In the left-hand figure, the Z_a arm has a shunt capacitor, C_a, and the Z_b arm has a series capacitor, C_b. Consequently, Z_a consists of C_a in parallel with Z_a′, and Z_b consists of C_b in series with Z_b′. This can be developed into the unbalanced bridged-T shown, provided C_a > C_b.

(An alternative version of this circuit has the T configuration of capacitors replaced by a Pi (or Delta) arrangement. For this T to Pi conversion, see the equations in Attenuator (electronics)).

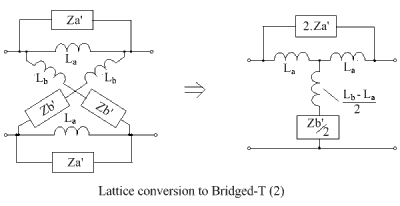
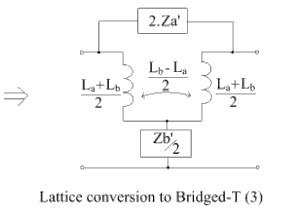
When C_b > C_a, an alternative procedure is necessary, where common inductors are first extracted from the lattice arms. As shown, an inductor L_a shunts Z_a′ and an inductor L_b is in series with Z_b′. This leads to the alternative bridged-T circuit on the right.

If L_a > L_b, then the negative-valued inductor can be achieved by means of mutually coupled coils. To achieve a negative mutual inductance, the two coupled inductors L1 and L2 are wound 'series-aiding'.

So finally, the bridged-T circuit takes the form

Bridged-T circuits like these may be used in delay and phase-correcting networks.

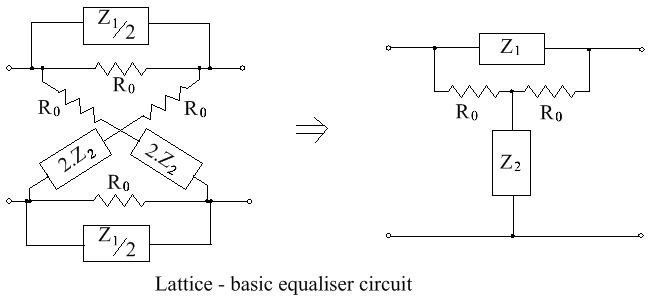
Another lattice configuration, containing resistors, is shown below. It has shunt resistors Ro across the Z_a’s and series resistors Ro as part of the Z_b's, as shown in the left hand figure. It is easily converted to an unbalanced bridged-T circuit, as shown on the right.

When Z₁Z₂ = R₀² it becomes a constant resistance network, which has an insertion loss given by [math]\displaystyle{ T(p) = \frac{R_0}{R_0 + Z_1(p)} }[/math]

When normalized to 1ohm, the source, load and R₀ are all unity, so Z₁.Z₂ = 1, and the insertion loss becomes

[math]\displaystyle{ T(p) = \frac{1}{1 + Z_1(p)} }[/math]

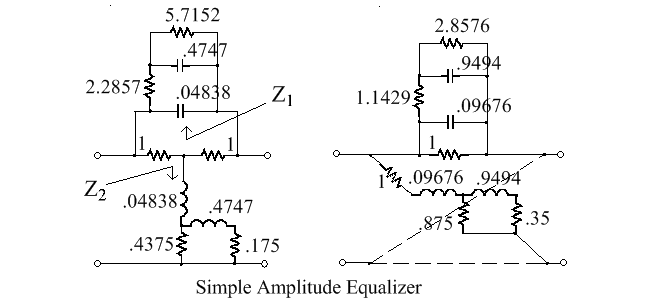
In the past, circuits configured in this way were very popular as amplitude equalisers. For example, they were used to correct for the high frequency losses in telephone cables and in long runs of coaxial cable for television installations.

An example, showing the design procedure for a simple equaliser, is given in the section on synthesis, later.

All-pass networks

(See previously quoted references to Zobel, Darlington, Bode and Guillemin. Also see Stewart and Weinberg.)

All-pass networks are an important sub-class of lattice networks. They have been used as passive lumped-element delays, as phase correctors for filter networks and in dispersive networks. They are constant-resistance networks so they can be cascaded with each other and with other circuits without introducing mismatch problems.

In the case of all-pass networks, there is no attenuation region, so the impedances Z_a and Z_b (of the lattice) are duals of each other at all frequencies and Z₀ is always resistive, equal to R₀.

i.e.,

[math]\displaystyle{ Z_a Z_b = R_0^2 \qquad \qquad \text{(at all frequencies)} }[/math]

For normalised networks, where R₀ = 1, the transfer function T(p) can be written

[math]\displaystyle{ T(p) = \frac{1-z_a(p)}{1+z_a(p)} = \frac{z_b(p)-1}{z_b(p)+1} }[/math]

and so

[math]\displaystyle{ z_a(p) = \frac{1-T(p)}{1+T(p)} \qquad \text{and} \qquad z_b(p) = \frac{1+T(p)}{1-T(p)} }[/math]

In practice, T(p) can be expressed as a ratio of polynomials in p, and the impedances z_a and z_b are also ratios of polynomials in p. For the impedances to be realisable, they must satisfy Foster's reactance theorem.

The two simplest all-pass networks are the first and second order lattices. These are important circuits because, as Bode pointed out, all high order all-pass lattice networks can be replaced by a cascade of second order networks with, possibly, one first order network, to give the identical response.

These two simple, normalised lattices have transfer impedances given by

[math]\displaystyle{ T_1(p)= \frac{-p+c}{p+c} \qquad \qquad \text{and} \qquad T_2(p) = \frac{p^2 -ap + b}{p^2 + ap +b} }[/math]

The circuits are considered in more detail in the section on 'Synthesis'

Lattice synthesis

Network synthesis is the process of deriving a circuit to match a chosen transfer function. Not all transfer functions can be realized by physical networks, but for those that can, the lattice network is always a solution. In other words, if a symmetrical two-terminal pair network is realizable at all, it is realizable as a lattice network. This is because the lattice structure is the most general form of a network, with fewer constraints than, say, T, П or bridged-T networks.

Once a lattice circuit has been developed, it is often desirable to convert the result into an unbalanced form, so that the circuit can be used in systems with an earth plane. Furthermore, there are other benefits to be gained from the conversion process, such as a reduced component count and less stringent component tolerances. Where a synthesis procedure results in several possible lattice solutions, the one that is easiest to convert is usually chosen. Often, the conversion process results in mutually coupled inductors, as shown earlier, but it is sometimes possible to avoid these altogether, if a high value of insertion loss can be tolerated, or if a combination of circuits in parallel is considered.

Synthesis with z parameters

z-parameters, or Impedance parameters, are one set from the family of parameters that define a two-port network, with input and output values defined by I₁, I₂, V₁ and V₂, as shown in the figure.

Two-port Network

Equations defining network behaviour in terms of z-parameters are

[math]\displaystyle{ \begin{align} E_1 = z_{11} I_1 + z_{12} I_2 \\ E_2 = z_{21} I_1 + z_{22} I_2 \end{align} }[/math]

where the z-parameters are defined under open circuit conditions (see Impedance parameters) so they are sometimes referred to as "open-circuit parameters". They are defined thus

[math]\displaystyle{ z_{11} = \left [\frac{V_1}{I_1} \right ] \text{ with } I_2 =0 \qquad \qquad z_{12} = \left [\frac{V_1}{I_2} \right ] \text{ with } I_1=0 }[/math]

[math]\displaystyle{ z_{21} = \left [\frac{V_2}{I_1} \right ] \text{ with } I_2 =0 \qquad \qquad z_{22} = \left [\frac{V_2}{I_2} \right ] \text{ with } I_1=0 }[/math]

For the symmetrical lattice, the relationships between z-parameters and the lattice impedances are easily found, and they are

[math]\displaystyle{ z_{11}=z_{22}= \frac{Z_a +Z_b}{2} \qquad z_{12}=z_{21}= \frac{Z_b-Z_a}{2} }[/math]

[math]\displaystyle{ Z_I=\sqrt{Z_a Z_b} }[/math]

So, [math]\displaystyle{ Z_a = z_{11}-z_{12} \, , \quad Z_b = z_{11} + z_{12} }[/math]

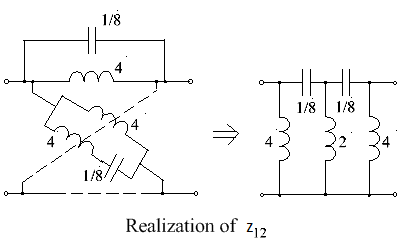
Sometimes synthesis of a lattice can be achieved by simply apportioning parts of an expression in z₁₂, or in z₁₁ and z₁₂, directly to the impedances Z_a and Z_b, as in the following example.

Example 1

Consider z₁₂ to be given by

[math]\displaystyle{ z_{12}=\frac{p^5}{(p^2+1)(p^2+2)} }[/math]

This can be expanded into partial fractions, to give

[math]\displaystyle{ z_{12}=\frac{p}{p^2+1} - \frac{4p}{p^2+2} + p }[/math]

Allocate terms to Z_a and Z_b, accordingly, so giving

[math]\displaystyle{ Z_a = \frac{8p}{p^2+2} }[/math] and [math]\displaystyle{ Z_b = \frac{2p}{p^2+1} +2p = \frac{2p^3+4p}{p^2+1} }[/math]

The lattice network which has these solutions for Z_a and Z_b is shown in the left-hand circuit, below. It can be converted to an unbalanced form by, firstly, extracting the common parallel inductors and, secondly, by then extracting series common capacitors. This gives the ladder network shown in the right-hand circuit.

Synthesis from the open-circuit transfer function

The open-circuit voltage-ratio transfer function T can be obtained in terms of z₁₁ and z₁₂, since with I₂ = 0

[math]\displaystyle{ T = \frac{V_2}{V_1} = \frac{z_{12}}{z_{11}} }[/math]

so from an expression for T, which gives the ratio of z_12, and z₁₁, it may be possible to obtain circuits for Z_a and Z_b.

In practice, T may be expressed in the form

[math]\displaystyle{ T(p) = K \cdot \frac{N(p)}{D{p}} }[/math]

where N(p) and D(p) are polynomials in p, the complex frequency variable, and K is a constant factor less or equal to unity.

For a given expression for T, it is often possible to find expressions (and hence circuits for Z_a and Z_b), provided the value chosen for K is small enough.

Now, for the lattice, [math]\displaystyle{ T = \frac{z_{11}}{z_{12}} = \frac{Z_b - Z_a}{Z_b + Z_a} = \frac {1-\frac{Z_a}{Z_b}}{1 + \frac{Z_a}{Z_b}} }[/math]

Rearranging [math]\displaystyle{ \frac{Z_a}{Z_b} = \frac{1-T}{1+T} = \frac{D-KN}{D+KN} }[/math]

The procedure evaluates the numerator and denominator of the expression as polynomials in p and then apportions factors to Z_a and Z_b. A loss term K, with K < 1, may be needed to aid realization.

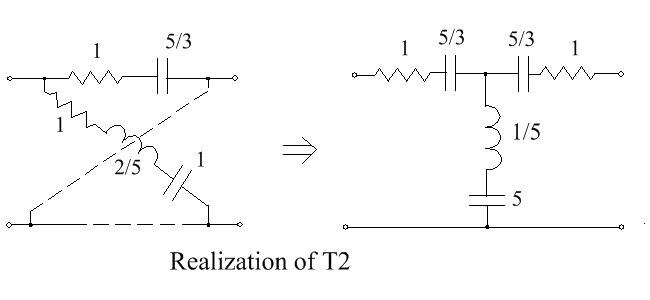
Example 2

Derive a lattice network with voltage-ratio transfer function T₂ given by

[math]\displaystyle{ T_2=K \cdot \frac{p^2+1}{p^2+5p+4} }[/math] with [math]\displaystyle{ K = 1 }[/math] and [math]\displaystyle{ \begin{align} D - KN &= p^2 + 5p +4 - p^2 -1 = 5p +3 \\ D + KN &= p^2 +5p + 4 +p^2 +1 = 2p^2 + 5p + 5 \end{align} }[/math] [math]\displaystyle{ \frac{Z_a}{Z_b} = \frac{5p+3}{2p^2 + 5p +5} = \frac{1+ 3/5p}{1+ (2p^2+5)/5p} }[/math]

Choose [math]\displaystyle{ Z_a = 1 + \frac{3}{5p} }[/math] and [math]\displaystyle{ Z_b = 1 +\frac{2p}{5} +\frac{1}{p} }[/math]

The lattice realization of T₂ is shown below, on the left. The unbalanced network, on the right, is obtained by first extracting the common series resistors and then extracting capacitance.

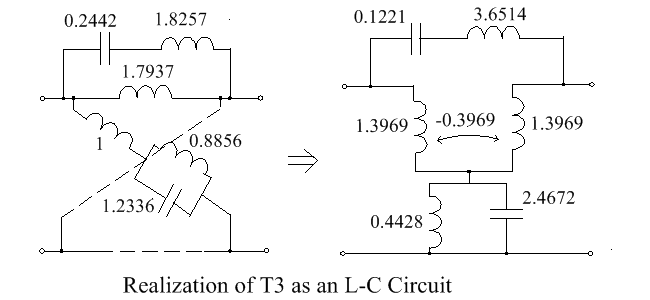
Example 3

An L-C circuit has a transfer function T₃ given by

[math]\displaystyle{ T_3 = K \cdot \frac{(p^4+1)}{(p^2+1)(p^2+2)} }[/math]

This is realizable with K = 0.05, so

[math]\displaystyle{ \frac{D - KN}{D + KN} = \frac{0.95(p^4 + 3.1579p^2 + 2.0526}{1.05(p^4 + 2.8571p^2 + 1.9524} = \frac{Z_a}{Z_b} }[/math]

Factorizing top and bottom gives

[math]\displaystyle{ \frac{Z_a}{Z_b} = \frac{0.95(p^2 + 0.9153)(p^2 + 2.2426)}{11.05(p^2 + 1.1312)(p^2 + 1.7259)} }[/math]

Choose, say,

[math]\displaystyle{ Z_a = \frac{0.9048(p^2 + 2.2426)}{(p^ + 1.1312)} \qquad \text{and} \qquad Z_b = \frac{p(p + 1.7259)}{p^2 + 0.9153} }[/math]

Z_a and Z_b can be realized as LC ladder networks, with Z_a having a shunt inductor as first element and Z_b having a series inductor as first element, as shown in the left-hand figure. This lattice can be converted to unbalanced form, by the methods given earlier, to give the component values of the right-hand figure,

Darlington synthesis

The Darlington method forms the basis for synthesis of lossless two terminal-pair networks with resistive termination for prescribed transfer characteristics.

Network for Darlington's Method

The figure shows the basic network configuration. The associated transfer impedance is

[math]\displaystyle{ T = \frac{E_2}{I_1} }[/math]

The first step is to express the input impedance Z_I of a terminated network in terms of its z-parameters. This is

[math]\displaystyle{ Z_I = \frac{(z_{11} z_{22} - z^{2}_{12}) + z_{11} R}{z_{22} + R} }[/math]

in which z₁₁, z₂₂ and z₁₂ are z-parameters of the network, as defined earlier. For a normalized network, put R = 1, and rearrange the expression thus:

[math]\displaystyle{ Z_I = z_{11} \cdot \frac{(z_{11} z_{22} - z^{2}_{12})/z_{11} +1}{z_{22} +1} }[/math]

In practice, Z_I consists of a ratio of two polynomials in p:

[math]\displaystyle{ Z_I = \frac{N(p)}{D(p)} = \frac{m_1 +n_1}{m_2 +n_2} }[/math]

where m₁ and n₁ are the even and odd parts of the numerator polynomial, respectively and m₂ and n₂ are the even and odd parts of the denominator polynomial, respectively.

Rearranging [math]\displaystyle{ Z_I = \frac{m_1}{n_2}\cdot\frac{(n_1/m_1) + 1}{(m_2/n_2) + 1} }[/math]

By comparing the two expressions for Z_I, the following relationships are suggested

[math]\displaystyle{ z_{11}=\frac{m_1}{n_2} \qquad \qquad z_{22} = \frac{m_2}{n_2} \qquad \qquad z_{12} = \frac{\sqrt{m_1 m_2 - n_1 n_2}}{n_2} }[/math]

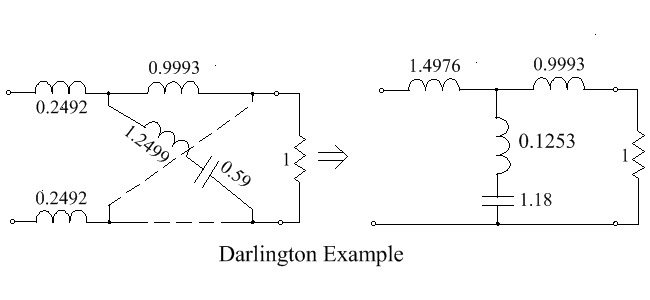
Example 4

Consider a network with Z_I given by

[math]\displaystyle{ Z_I = \frac{2.1351p^3 + 1.915p^2 + 2.4969p + 1}{1.327p^2 +1.18p +1} }[/math] So, [math]\displaystyle{ \begin{align} m_1 &= 1.915p^2 +1 & n_1 &= 2.1351p^3 + 1\\ m_2 &= 1.327p^2 +1 & n_2 &= 1.18p \end{align} }[/math]

So solutions for z₁₁, z₂₂ and z₁₂ are [math]\displaystyle{ z_{11} = \frac{1.915p^2 + 1}{1.18p} = 1.6229p + \frac{1}{1.18p} }[/math]

i.e. z₁₁ is an inductor of 1.6229H in series with a capacitor of 1.18F.

[math]\displaystyle{ z_{22} = \frac{1.327p^2 + 1}{1.18p} = 1.1246p + \frac{1}{1.18} }[/math]

i.e. z₂₂ is an inductor of 1.1246H in series with a capacitor of 1.18F

[math]\displaystyle{ \begin{align} z_{12} &= \frac{\sqrt{(1.915p^2 +1)(1.327p^2 +1) -(2.1351p^3 + 2.4969p)}}{1.18p} \\ &= \frac{\sqrt{0.0218p^4 + 0.2957p^2 +1}}{1.18p}\quad = \frac{0.1479p^2 +1}{1.18p} \quad = 0.1253p + \frac{1}{1.18p} \end{align} }[/math]

By extracting a series inductance of 0.4983p = (1.6229p – 1.1246p) from z₁₁, the remaining network becomes symmetrical with

[math]\displaystyle{ \begin{align} z_{11}^\text{(new)} = z_{22} = 1.1246p + \frac{1}{1.18p} \\ z_{12} = 0.1253p + \frac{1}{1.18p} \end{align} }[/math]

The components of a symmetrical lattice can be calculated from Z_a = z₁₁ − z₁₂ and Z_b = z₁₁ + z₁₂.

So [math]\displaystyle{ Z_a=1.1246p + \frac{1}{1.18p} - 0.1253p - \frac{1}{1.18p} = 0.9993p, }[/math] i.e. an inductor of 0.9993H.

and [math]\displaystyle{ Z_b = 1.1246p + \frac{1}{1.18p} + 0.1253p + \frac{1}{1.18p} = 1.2499p + \frac{2}{1.18p}, }[/math] i.e. an inductor of 1.2499H in series with a capacitor of 0.59F

The circuit is shown in the left hand figure below. It can be easily converted into the unbalanced form shown in the right hand figure. It is a low-pass filter with pass-band ripple of 1.25 dB, with −3 dB at 0.169 Hz, a null in the stop band at 0.414 Hz, and stop-band attenuation beyond the null frequency below −40 dB.

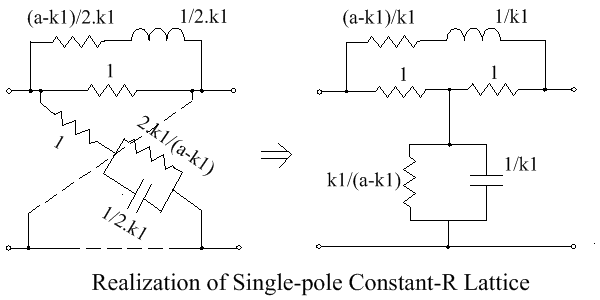
Synthesis of constant-resistance lattice networks

If the impedances Z_a and Z_b are duals, and normalised, so that

[math]\displaystyle{ Z_a Z_b = 1 }[/math]

then the image impedance Z_I becomes a pure resistance. A symmetrical lattice fulfilling this condition is a "constant resistance lattice".

Such a lattice, terminated in 1 ohm, is shown below.

Terminated Constant-R Lattice

This has the transfer function

[math]\displaystyle{ \frac{E_2}{E_1} = \frac{E_2}{I_1} = T =\frac{1 - Z_a}{1 + Z_a} }[/math]

in which T is the transfer impedance with a 1-ohm load in contrast to the open-circuit transfer impedance z₂₁. Rearranging this, gives

[math]\displaystyle{ Z_a = \frac{1 -T}{1 + T} }[/math]

The constant resistance lattice is thus seen to offer a possible approach to the synthesis of transfer functions.

It is the case that a constant resistance lattice is no less general than any other lattice, which means that any realizable transfer impedance can be realized in the form of a constant resistance lattice,. Such networks are very convenient, because there is no mismatch between sections or with resistive terminations. Consequently, the overall insertion loss of a cascade of constant resistance sections is simply to sum total of the individual sections. Conversely, a given complicated transfer impedance may be decomposed into multiplicative factors, whose individual lattice realizations, when connected in cascade, represent a synthesis of that transfer impedance. So, although it is possible to synthesize a single lattice with complicated impedances Z_a and Z_b, it is practically easier to construct and align a cascade of simpler circuits.

All-pass constant-resistance networks

All-pass networks have a constant gain with frequency, but they have a phase response which varies in some chosen manner. For example, in the case of lattice delay networks, the phase response is linear with frequency over a specified frequency range, whereas in the case of Lattice phase equalisers, the phase response of the network deviates so as to compensate for the non-linear phase response of a filter network.

The first and second order networks are the most important because, as Bode pointed out, these can be cascaded, as required, to give the same result as a complicated high order lattice.

Example 5

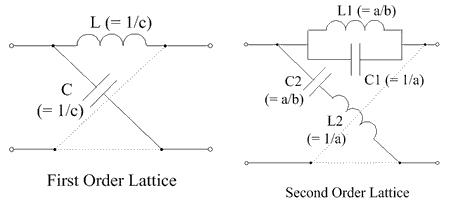
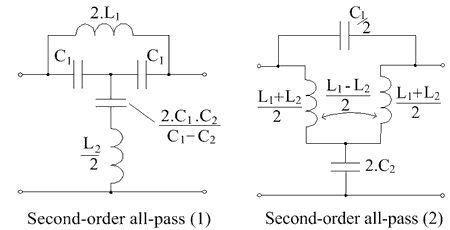
The all-pass response of the first order is

[math]\displaystyle{ T_5 = \frac{c - p}{c + p} }[/math]

This has a zero located at +c and a pole at –c in the complex frequency plane. It has a response where the phase varies with frequency, but the magnitude of T₅ is unity at all frequencies.

Using the expression for Z_a as a function of T, from earlier, gives

[math]\displaystyle{ Z_a = \frac{1 - T_5}{1 + T_5} = \frac{p}{c} }[/math]

So Z_a is an inductance with value 1/c and, consequently, Z_b is a capacitor of value 1/c. The network, normalised to 1 ohm, is shown in the left-hand figure below.

Example 6

The all-pass response of the second order is

[math]\displaystyle{ T_6 = \frac{p^2 - ap +b}{p^2 + ap +b} }[/math]

This has two zeroes located at [math]\displaystyle{ x \pm y }[/math] and two poles at [math]\displaystyle{ -x \pm y }[/math] where a = 2x and b = x² + y². For such a response, the phase varies with frequency, but the magnitude of T₆ is unity at all frequencies.

For this characteristic, Z_a is found from

[math]\displaystyle{ Z_a = \frac{1 - T_6}{1+T_6} = \frac{ap}{p^2 + b} }[/math]

So Z_a is a parallel combination of a capacitance 1/a and an inductance with value a/b. Similarly Z_b is an inductor 1/a in series with a capacitor of value a/b and the network is shown at the right hand side below.

The lattice networks can be converted to unbalanced circuits by using the properties of lattices with common elements in both Z_a and Z_b, shown earlier, and Bartlett’s Bisection theorem.

First order all-pass

In the case of the second order network, when a2 > b (i.e. L1 > L2 or C2 > C1 or y > √3x), it is necessary to use the circuit containing mutually coupled coils for the second order all-pass network.

A cascade of second order networks with, maybe, a single first order network, can be used to give a high order response. For example, the article Lattice delay network gives pole-zero locations for many all-pass transfer functions which approximate to a linear phase characteristic. That article also includes some examples.

Synthesis of amplitude equalizers

A typical transmission path has increasing loss with frequency and this can be corrected by cascading the system with an equalizing network that has a rising response with frequency. In this regard, one circuit configuration that is commonly used to provide the necessary equalization is shown in the figure labelled 'Lattice - basic equaliser circuit', given earlier (in the section on 'Unbalanced Equivalents'). As stated there, the insertion loss of the normalized circuit is given by [math]\displaystyle{ T= \frac{1}{1+Z_1(p)} }[/math], so Z₁ can be found from [math]\displaystyle{ Z_1(p) = \frac{1}{T(p)} - 1 }[/math]

If some residual ripple on the response is permitted, then a simple correcting network may suffice for Z₁ and Z₂, but this ripple may be reduced as much as desired by adopting more complicated correcting networks. Choosing locations for the poles and zeros for Z₁ and Z₂ may be aided by the straight line asymptotic method.

Example 7

A transfer function which has a rising response over a limited frequency range is

[math]\displaystyle{ T_7(p) = \frac{3.3333 + 10.3333p + p^2}{30.003 + 31.003p + p^2}= \frac{(0.3333 + p)(10 + p)}{(1 + p)(30.003 + p)} }[/math]

Note that the response approaches unity at high frequencies. It can be realized as a bridged-T or lattice in which Z₁ is an R-C network.

Z₁ can be found from [math]\displaystyle{ Z_1(p) = \frac{1}{T(p)} -1 }[/math]. So [math]\displaystyle{ Z_1(p) = \frac{26.6697 + 20.6697p}{3.3333 + 10.3333p + p^2} }[/math]

The admittance Y₁, where Y₁ = 1/Z₁ can be expressed as a continued fraction containing four terms, thus

[math]\displaystyle{ Y_1(p) = \frac{p^2 + 10.333p + 3.3333}{20.6697p + 26.6697} = 0.04838 + \cfrac{1}{2.2857 + \cfrac{1}{0.4747p + \cfrac{1}{5.7153}}} }[/math]

So Z₁ can be realized as an R-C ladder network, in the Cauer manner, and is shown as part of the bridged-T circuit below. Z₂ is the dual of Z₁, and so is an R-L circuit, as shown. The equivalent lattice circuit is shown on the right–hand side.

Constant resistance low-pass filters

High order low-pass filters can be obtained by cascading an appropriate number of simpler constant resistance low-pass sections.

The first of these low-pass sections, with just a single pole, has the response

[math]\displaystyle{ T_1 = \frac{k_1}{p+a} \qquad so \qquad Z_{a 1}=\frac{1-T_1}{1+T_1} = \frac{p + (a - k_1)}{p + (a + k_1)} }[/math]

Provided [math]\displaystyle{ k_1 \le a }[/math] this is realizable impedance, where Z_a1 is a combination of two resistors and an inductor, as shown in the left-hand circuit below, and Z_b1 is the dual of Z_a1. This is easily transformed into an unbalanced form, as shown on the right.

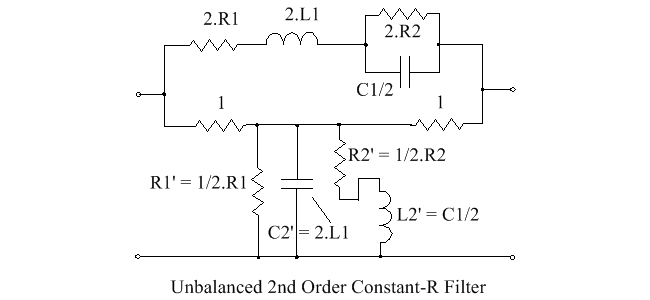
The second of the filter sections, with two poles, has the response

[math]\displaystyle{ T_2 = k_2\frac{(p + a)}{(p^2 +b_1p + b_0)} }[/math]

So the lattice impedance Z_a2 is given by:

[math]\displaystyle{ Z_{a2} = \frac{p^2 + (b_1 - k_2)p + (b_0 - a.k_2)}{p^2 + (b_1 + k_2)p + (b_0 + a.k_2)} }[/math]

Certain conditions have to be met to ensure this is a realizable network, which are [math]\displaystyle{ a \ge 0; \qquad k_2 \le b_1; \qquad k_2 \le \frac{b_0}{a}. }[/math] Also [math]\displaystyle{ b_1 - k_2 \iff k_2 \le b_1 - a. }[/math]

The conditions set limits on the value of the constant multiplier k₂ in the expression for T₂.

The circuit for the lattice elements Z_a2 is shown on the left, below, and that for the dual elements Z_b is shown on the right.

Impedance Z_a

Impedance Zb

Component values for Z_a are, [math]\displaystyle{ \begin{align} R_1 &= \frac{b_1 - k_2 - a}{2k_2} & L &= \frac{1}{2k_2} \\ C &= \frac{2k_2}{b_0 -ab_1 +a^2}{2ak_2} & R_2 &= \frac{b_0 -ab_1 + a^2}{2ak-2} \end{align} }[/math]

and those for the impedances Z_b2 are: [math]\displaystyle{ \begin{align} R_3 &= \frac{1}{R_1} \\ R_4 &= \frac{1}{R_2} \\ C_2 &= L_1 \quad \text{and} \quad L_2 + C_1 \end{align} }[/math]

The unbalanced version of this lattice is as shown below:

By cascading a number of the first and second order circuits, of the type just developed, it is possible to derive higher order low-pass networks of the type:

[math]\displaystyle{ T_n(p) = \frac{k}{p^n + b_{n - 1} p^{n - 1}+ \cdots + b_2 p^2 +b_1 p +b_0} }[/math]

The lattice networks so obtained can be converted to an unbalanced form, provided the value of k is sufficiently small.

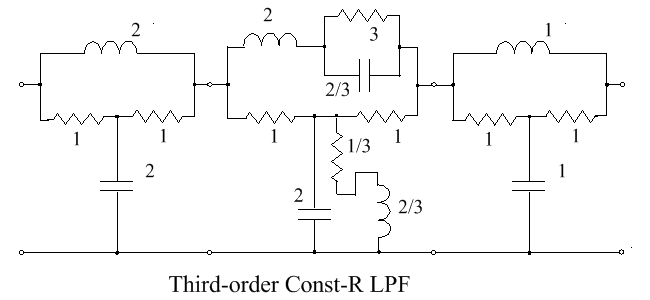
Example 8

A maximally flat third-order normalized low pass filter has the transfer function

[math]\displaystyle{ T_8 = \frac{k}{p^3 + 2p^2 + 2p +1} }[/math]

This can be expanded as

[math]\displaystyle{ T_8 = \frac{k_1}{p + a} \cdot \frac{k_2(p + a)}{p^2 + p + 1} \cdot \frac{1}{p + 1} }[/math]

So a cascade of three lattices will give the required result.

If an unbalanced circuit is required, we have to accept some overall loss. By choosing k₁ = k₂ = a = 0.5, then the network shown below is obtained. This circuit has an overall loss of four times, whereas the conventional L-C ladder network has no loss (but is not a constant resistance network).

Computer-aided design methods

The development of mainframe and then personal computers, in the final quarter of the twentieth century, permitted the rapid development of numerical processing techniques. Initially, computers were used as an aid to network analysis then to optimization methods such as the minimax method, in the design of phase equalizers and filters), before being applied to network synthesis directly. Overviews of the software developments in the field of synthesis have been given in Taylor & Huang and Kuo.

Only a few of the early synthesis programs have dealt with lattice networks, but S-Filsyn (a powerful synthesis and analysis program ) provides some coverage of lattice and bridged-T circuits.

Early history

The symmetrical lattice and the ladder networks (the constant k filter and m-derived filter), were the subject of much interest in the early part of the twentieth century. At that time, the rapidly growing telephone industry had a significant influence on the development of filter theory, while seeking to increase the signal carrying capacity of telephone transmission lines. George Ashley Campbell was a key contributor to this new filter theory, as was Otto Julius Zobel. They and many colleagues worked at the laboratories of Western Electric and the American Telephone and Telegraph Co., and their work was reported in the early editions of the Bell System Technical Journal.

Campbell discussed lattice filters in his article of 1922, while other early workers with an interest in the lattice included Johnson and Bartlett. Zobel's article on filter theory and design, published at about this time, mentioned lattices only briefly, with his main emphasis on ladder networks. It was only later, when Zobel considered the simulation and equalisation of telephone transmission lines, that he gave the lattice configuration more attention. (The telephone transmission lines of the time had a balanced-pair configuration with a nominal characteristic impedance of 600 ohms, so the lattice equaliser, with its balanced structure, was particularly appropriate for use with them). Later workers, especially Hendrik Wade Bode, gave greater prominence to lattice networks in their filter designs.

In those early days, filter theory was based on image impedance concepts, or image filter theory, which was a design approach developed from the well-established studies of transmission lines. The filter was considered to be a lumped component version of a section of transmission line, and was one of many within a cascade of similar sections. As mentioned above, the weakness of the image filter approach was that the frequency response of a network was often not as predicted when the network was terminated resistively, instead of by the required image impedances. This was essentially a mismatch issue and Zobel overcame it by means of matching end sections. (see: m-derived filter, mm'-type filter, General mn-type image filter, with later work by Payne and Bode.)

Although lattice filters sometimes suffer from this same problem, a range of constant-resistance networks can avoid it altogether.

During the 1930s, as techniques in network analysis and synthesis became better developed, designing ladder filters by image methods became less popular. Even so, the concepts still found relevance in some modern designs. On the other hand, lattice networks and their circuit equivalents continue to be used in many applications.

See also

• Lattice phase equalizer
• All-pass filter
• Two-port network
• Composite image filter
• Lattice delay network
• Ladder network