Coordinate systems for the hyperbolic plane
In the hyperbolic plane, as in the Euclidean plane, each point can be uniquely identified by two real numbers. Several qualitatively different ways of coordinatizing the plane in hyperbolic geometry are used. This article tries to give an overview of several coordinate systems in use for the two-dimensional hyperbolic plane.
In the descriptions below the constant Gaussian curvature of the plane is −1. Sinh, cosh and tanh are hyperbolic functions.
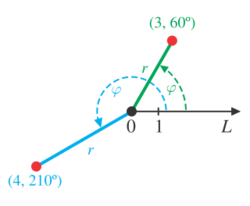
Polar coordinate system
The polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction.
The reference point (analogous to the origin of a Cartesian system) is called the pole, and the ray from the pole in the reference direction is the polar axis. The distance from the pole is called the radial coordinate or radius, and the angle is called the angular coordinate, or polar angle.
From the hyperbolic law of cosines, we get that the distance between two points given in polar coordinates is
- [math]\displaystyle{ \operatorname{dist} (\langle r_1, \theta_1 \rangle, \langle r_2, \theta_2 \rangle) = \operatorname{arcosh} \, \left( \cosh r_1 \cosh r_2 - \sinh r_1 \sinh r_2 \cos (\theta_2 - \theta_1) \right) \,. }[/math]
The corresponding metric tensor field is: [math]\displaystyle{ (\mathrm{d} s)^2 = (\mathrm{d} r)^2 + \sinh^2 r \, (\mathrm{d} \theta)^2 \,. }[/math]
The straight lines are described by equations of the form
- [math]\displaystyle{ \theta = \theta_0 \pm \frac{\pi}{2} \quad \text{ or } \quad \tanh r = \tanh r_0 \sec (\theta - \theta_0) }[/math]
where r0 and θ0 are the coordinates of the nearest point on the line to the pole.
Quadrant model system
The Poincaré half-plane model is closely related to a model of the hyperbolic plane in the quadrant Q = {(x,y): x > 0, y > 0}. For such a point the geometric mean [math]\displaystyle{ v = \sqrt {x y} }[/math] and the hyperbolic angle [math]\displaystyle{ u = \ln \sqrt {x/y} }[/math] produce a point (u,v) in the upper half-plane. The hyperbolic metric in the quadrant depends on the Poincaré half-plane metric. The motions of the Poincaré model carry over to the quadrant; in particular the left or right shifts of the real axis correspond to hyperbolic rotations of the quadrant. Due to the study of ratios in physics and economics where the quadrant is the universe of discourse, its points are said to be located by hyperbolic coordinates.
Cartesian-style coordinate systems
In hyperbolic geometry rectangles do not exist. The sum of the angles of a quadrilateral in hyperbolic geometry is always less than 4 right angles (see Lambert quadrilateral). Also in hyperbolic geometry there are no equidistant lines (see hypercycles). This all has influences on the coordinate systems.
There are however different coordinate systems for hyperbolic plane geometry. All are based on choosing a real (non ideal) point (the Origin) on a chosen directed line (the x-axis) and after that many choices exist.
Axial coordinates
Axial coordinates xa and ya are found by constructing a y-axis perpendicular to the x-axis through the origin.[1]
Like in the Cartesian coordinate system, the coordinates are found by dropping perpendiculars from the point onto the x and y-axes. xa is the distance from the foot of the perpendicular on the x-axis to the origin (regarded as positive on one side and negative on the other); ya is the distance from the foot of the perpendicular on the y-axis to the origin.
Every point and most ideal points have axial coordinates, but not every pair of real numbers corresponds to a point.
If [math]\displaystyle{ \tanh^2 (x_a) + \tanh^2 (y_a) = 1 }[/math] then [math]\displaystyle{ P(x_a , y_a) }[/math] is an ideal point.
If [math]\displaystyle{ \tanh^2 (x_a) + \tanh^2 (y_a) \gt 1 }[/math] then [math]\displaystyle{ P(x_a , y_a) }[/math] is not a point at all.
The distance of a point [math]\displaystyle{ P(x_a , y_a) }[/math] to the x-axis is [math]\displaystyle{ \operatorname {artanh} \left( \tanh(y_a) \cosh(x_a) \right) }[/math]. To the y-axis it is [math]\displaystyle{ \operatorname{artanh} \left( \tanh(x_a) \cosh(y_a) \right) }[/math].
The relationship of axial coordinates to polar coordinates (assuming the origin is the pole and that the positive x-axis is the polar axis) is
- [math]\displaystyle{ x = \operatorname {artanh} \, (\tanh r \cos \theta) }[/math]
- [math]\displaystyle{ y = \operatorname {artanh} \, (\tanh r \sin \theta) }[/math]
- [math]\displaystyle{ r = \operatorname {artanh} \, (\sqrt{\tanh^2 x + \tanh^2 y} \, ) }[/math]
- [math]\displaystyle{ \theta = 2 \operatorname {arctan} \, \left( \frac{\tanh y}{\tanh x + \sqrt{\tanh^2 x + \tanh^2 y} } \right) \,. }[/math]
Lobachevsky coordinates
The Lobachevsky coordinates xℓ and yℓ are found by dropping a perpendicular onto the x-axis. xℓ is the distance from the foot of the perpendicular to the x-axis to the origin (positive on one side and negative on the other, the same as in axial coordinates).[1]
yℓ is the distance along the perpendicular of the given point to its foot (positive on one side and negative on the other).
- [math]\displaystyle{ x_l = x_a \ , \ \tanh(y_l) = \tanh(y_a) \cosh(x_a) \ , \ \tanh(y_a) = \frac{\tanh(y_l)}{\cosh(x_l)} }[/math].
The Lobachevsky coordinates are useful for integration for length of curves[2] and area between lines and curves.[example needed]
Lobachevsky coordinates are named after Nikolai Lobachevsky one of the discoverers of hyperbolic geometry.
Construct a Cartesian-like coordinate system as follows. Choose a line (the x-axis) in the hyperbolic plane (with a standardized curvature of -1) and label the points on it by their distance from an origin (x=0) point on the x-axis (positive on one side and negative on the other). For any point in the plane, one can define coordinates x and y by dropping a perpendicular onto the x-axis. x will be the label of the foot of the perpendicular. y will be the distance along the perpendicular of the given point from its foot (positive on one side and negative on the other). Then the distance between two such points will be
- [math]\displaystyle{ \operatorname{dist} (\langle x_1, y_1 \rangle, \langle x_2, y_2 \rangle) = \operatorname{arcosh} \left( \cosh y_1 \cosh (x_2 - x_1) \cosh y_2 - \sinh y_1 \sinh y_2 \right) \,. }[/math]
This formula can be derived from the formulas about hyperbolic triangles.
The corresponding metric tensor is: [math]\displaystyle{ (\mathrm{d} s)^2 = \cosh^2 y \, (\mathrm{d} x)^2 + (\mathrm{d} y)^2 }[/math].
In this coordinate system, straight lines are either perpendicular to the x-axis (with equation x = a constant) or described by equations of the form
- [math]\displaystyle{ \tanh y = A \cosh x + B \sinh x \quad \text{ when } \quad A^2 \lt 1 + B^2 }[/math]
where A and B are real parameters which characterize the straight line.
The relationship of Lobachevsky coordinates to polar coordinates (assuming the origin is the pole and that the positive x-axis is the polar axis) is
- [math]\displaystyle{ x = \operatorname {artanh} \, (\tanh r \cos \theta) }[/math]
- [math]\displaystyle{ y = \operatorname {arsinh} \, (\sinh r \sin \theta) }[/math]
- [math]\displaystyle{ r = \operatorname {arcosh} \, (\cosh x \cosh y) }[/math]
- [math]\displaystyle{ \theta = 2 \operatorname {arctan} \, \left( \frac{\sinh y}{\sinh x \cosh y + \sqrt{\cosh^2 x \cosh^2 y - 1} } \right) \,. }[/math]
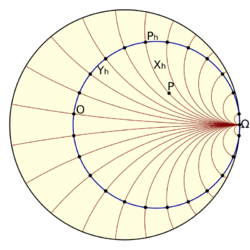
Horocycle-based coordinate system
Another coordinate system uses the distance from the point to the horocycle through the origin centered around [math]\displaystyle{ \Omega = (0, + \infty ) }[/math][clarification needed] and the arclength along this horocycle.[3]
Draw the horocycle hO through the origin centered at the ideal point [math]\displaystyle{ \Omega }[/math] at the end of the x-axis.
From point P draw the line p asymptotic to the x-axis to the right ideal point [math]\displaystyle{ \Omega }[/math]. Ph is the intersection of line p and horocycle hO.
The coordinate xh is the distance from P to Ph[clarification needed] – positive if P is between Ph and [math]\displaystyle{ \Omega }[/math], negative if Ph is between P and [math]\displaystyle{ \Omega }[/math].
The coordinate yh is the arclength along horocycle hO from the origin to Ph.[clarification needed]
The distance between two points given in these coordinates is
- [math]\displaystyle{ \operatorname{dist} (\langle x_1, y_1 \rangle, \langle x_2, y_2 \rangle) = \operatorname{arcosh} ( \cosh (x_2 - x_1) + \tfrac12 (y_2 - y_1)^2 \exp (- x_1 - x_2) ) \,. }[/math]
The corresponding metric tensor is: [math]\displaystyle{ (\mathrm{d} s)^2 = (\mathrm{d} x)^2 + \exp (-2 x) \, (\mathrm{d} y)^2 \,. }[/math]
The straight lines are described by equations of the form y = a constant or
- [math]\displaystyle{ x = \tfrac12 \ln ( \exp (2 x_0) - (y - y_0)^2 ) }[/math]
where x0 and y0 are the coordinates of the point on the line nearest to the ideal point [math]\displaystyle{ \Omega }[/math] (i.e. having the largest value of x on the line).
Model-based coordinate systems
Model-based coordinate systems use one of the models of hyperbolic geometry and take the Euclidean coordinates inside the model as the hyperbolic coordinates.
Beltrami coordinates
The Beltrami coordinates of a point are the Cartesian coordinates of the point when the point is mapped in the Beltrami–Klein model of the hyperbolic plane, the x-axis is mapped to the segment (−1,0) − (1,0) and the origin is mapped to the centre of the boundary circle.[1]
The following equations hold:
- [math]\displaystyle{ x_b = \tanh (x_a), \ y_b = \tanh(y_a) }[/math]
Poincaré coordinates
The Poincaré coordinates of a point are the Cartesian coordinates of the point when the point is mapped in the Poincaré disk model of the hyperbolic plane,[1] the x-axis is mapped to the segment (−1,0) − (1,0) and the origin is mapped to the centre of the boundary circle.
The Poincaré coordinates, in terms of the Beltrami coordinates, are:
- [math]\displaystyle{ x_p = \frac{x_b}{1+\sqrt{1 -x_b^2 - y_b^2 }}, \ \ y_p = \frac{y_b}{1+\sqrt{1 -x_b^2 - y_b^2 }} }[/math]
Weierstrass coordinates
The Weierstrass coordinates of a point are the Cartesian coordinates of the point when the point is mapped in the hyperboloid model of the hyperbolic plane, the x-axis is mapped to the (half) hyperbola [math]\displaystyle{ (t \ , \ 0 \ , \ \sqrt{t^2+1} ) }[/math] and the origin is mapped to the point (0,0,1).[1]
The point P with axial coordinates (xa, ya) is mapped to
- [math]\displaystyle{ \left( \frac{\tanh x_a}{\sqrt{1 -\tanh^2 x_a - \tanh^2 y_a }} \ , \ \frac{\tanh y_a}{\sqrt{1 -\tanh^2 x_a - \tanh^2 y_a }} \ , \ \frac{1}{\sqrt{1 -\tanh^2 x_a - \tanh^2 y_a }} \right) }[/math]
Others
Gyrovector coordinates
Hyperbolic barycentric coordinates
From Gyrovector space
The study of triangle centers traditionally is concerned with Euclidean geometry, but triangle centers can also be studied in hyperbolic geometry. Using gyrotrigonometry, expressions for trigonometric barycentric coordinates can be calculated that have the same form for both euclidean and hyperbolic geometry. In order for the expressions to coincide, the expressions must not encapsulate the specification of the anglesum being 180 degrees.[4][5][6]
References
- ↑ 1.0 1.1 1.2 1.3 1.4 Martin, George E. (1998). The foundations of geometry and the non-Euclidean plane (Corrected 4. print. ed.). New York, NY: Springer. pp. 447–450. ISBN 0387906940. https://archive.org/details/foundationsofgeo0000mart.
- ↑ Smorgorzhevsky, A.S. (1982). Lobachevskian geometry. Moscow: Mir. pp. 64–68.
- ↑ Ramsay, Arlan; Richtmyer, Robert D. (1995). Introduction to hyperbolic geometry. New York: Springer-Verlag. pp. 97–103. ISBN 0387943390. https://archive.org/details/introductiontohy0000rams.
- ↑ Hyperbolic Barycentric Coordinates, Abraham A. Ungar, The Australian Journal of Mathematical Analysis and Applications, AJMAA, Volume 6, Issue 1, Article 18, pp. 1–35, 2009
- ↑ Hyperbolic Triangle Centers: The Special Relativistic Approach, Abraham Ungar, Springer, 2010
- ↑ Barycentric Calculus In Euclidean And Hyperbolic Geometry: A Comparative Introduction , Abraham Ungar, World Scientific, 2010
 |